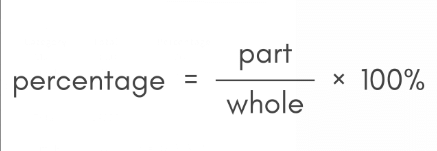Comparing Quantities Chapter Notes | Mathematics (Maths) Class 8 PDF Download
Recalling Ratios and Percentages
Ratio: A ratio is a way of comparing two or more quantities. For example, 2:3 is a ratio, which means for every two parts of one thing, there are three parts of another.
Percentages: A percentage is a number or ratio that can be expressed as a fraction of 100.
Ratios are a way to show how two quantities relate to each other. Imagine you have 5 green marbles and 2 pink marbles. If you want to compare the number of green marbles to the number of pink marbles, you use a ratio. Similarly, percentages help us easily understand how big or small a part is compared to the whole. So, if you see a 50% discount on a toy, it means the price is cut in half!
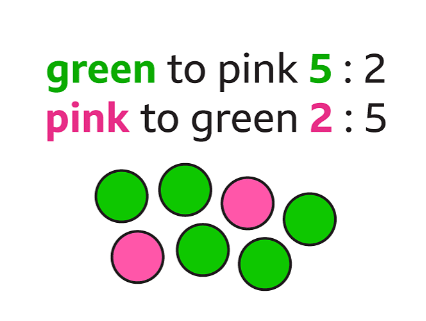 RatiosLets understand this with the help of an example:
RatiosLets understand this with the help of an example:
A basket contain 20 apples and 5 oranges.
1. Ratio of number of oranges to the number of apples = 5 : 20. (5 is to 20)
This means for every 5 oranges there exist 20 apples.
This can also be expressed as a fraction, which would be 5/20 or 1/4.
2. Percentage of apples = (Total number of apples / Total number of fruits)x100
=> (20/25)x100
=> 80%
Let's dive deeper into this topic by solving a detailed problem.
Example: A picnic is being planned in a school for class VIII. Girls are 60% of the total number of students and are 18 in number. The picnic site is 55km from the school and the transport company is charging at the rate of ₹ 12 per km. The total cost of refreshments will be ₹ 4280.
1. The ratio of the number of girls to the number of boys in the class?
Sol: Let the total number of students be n.
60% of the total number of students are girls. This can be written as:
=> n x 60/100 = 18
=> n = 30.
Number boys = 30 -18 = 12.
Ratio of girls to the boys = 18/12= 3/2.
2. The cost per head if two teachers are also going with the class?
Sol: Total expenses = Transportation charge + refreshment charge
Transportation charge can be calculated by multiplying the distance with the rate per kilometer given.
Total expenses => (55 x 12) + 4280
=>1320 + 4280 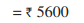
Total number of persons =18 girls + 12 boys + 2 teachers = 32 persons
The amount spent for one person 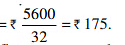
3. If their first stop is at a place 22 km from the school, what percent of the total distance of 55 km is this? What per cent of the distance is left to be covered?
Sol: Since bus stop at 22km from the school, the percentage of distance = (22/55)x 100
=>40%.
Total distance = 100%
covered distance = 40%
uncovered = 100-40=60%.
Finding Discounts
A discount is the reduction given on the Marked Price of the article.
Discount = Marked Price - Sale Price
Sol: Marked Price and List Price are same thing.
Since 20% is off then only 80% of List price a customer has to pay
Hence 80% of 220 = (80/100)x220 = ₹176
Estimation in Percentages
If a percentage is in decimal like 50.69% then we will round off the number to the nearest integer.
For example 50.69% = 51% if we round it off to the nearest tens.
Sales Tax/ Value Added Tax/ Goods and Services Tax
Imagine you're buying a toy that costs $100. But when you go to pay, the cashier asks for $110 instead of $100. Why? That's because of something called a sales tax or VAT.
Sales Tax/VAT is a little extra money you have to pay when you buy something. This extra money goes to the government so they can use it to build things like roads, schools, and hospitals. The percentage of the extra money can vary, so sometimes you pay a bit more or a bit less, depending on the kind of thing you are buying and from which area.
Total Bill = Actual Amount + Tax Amount



Example : (Finding Sales Tax) The cost of a pair of roller skates at a shop was ₹450. The sales tax charged was 5%. Find the bill amount.
Sol: Total Bill = ₹450 + tax
Tax = 450x(5/100) = ₹22.5
Total Bill = 450 + 22.5 = ₹472.50
Compound Interest
Let's first remember what simple interest is.
Simple interest is a way to calculate the extra money you earn or pay when you save or borrow money. It’s called "simple" because it’s easy to calculate and doesn’t change over time.
Formula for Simple Interest:
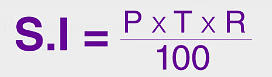
where,
- P= Principal is the original amount of money you save or borrow.
- R= Rate is the percentage of interest per year.
- T= Time is the number of years the money is saved or borrowed.
Example : A sum of ₹10,000 is borrowed at a rate of interest 15% per annum for 2 years. Find the simple interest on this sum and the amount to be paid at the end of 2 years.
Sol: Interest Charged For One Year = 
Interest for 2 years = ₹ 1500 × 2 = ₹3000 Amount to be paid at the end of 2 years = Principal + Interest = ₹ 10000 + ₹3000 = ₹13000
Calculating Compound Interest
Now, let's understand compound interest.
Compound interest is interest earned on the principal sum and previously accumulated interest. It's also known as "interest on interest".
 The formula for compound interest is as follows:
The formula for compound interest is as follows: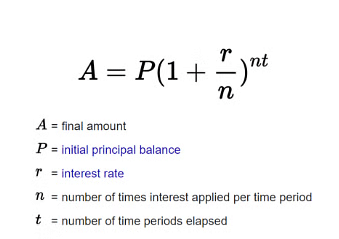
CI = Final Amount - Initial Amount
Deducing a Formula for Compound Interest
To better our understanding of the concept, let us take a look at the compound interest formula derivation. Here we will take our principal to be Rupee.1/- and work our way towards the interest amounts of each year gradually.
Year 1
The interest on Rupee 1/- for 1 year is equal to r/100 = i (assumed)
Interest after Year 1 is equal to Pi
FV (Final Value) after Year 1 is equal to P + Pi = P(1+i)
Year 2
Interest for Year 2 = P(1+i) × i
FV after year two is equal to P(1+i) + P(1+i) × i = P(1+i)2
Year ‘t’
Final Value (Amount) after year “t” is equal to P(1+i)t
Now substituting actual values we get Final Value is equal to ( 1 + R/100)t
CI = FV – P is equal to P ( 1 + R/100)t – P
This is how the formula of compound interest can be derived.
Applications of Compound Interest Formula
Some of the applications of compound interest are:
1. Increase in population or decrease in population.
2. Growth of bacteria.
3. Rise in the value of an item.
4. Depreciation in the value of an item.
Example: The value of a piece of art was $5,000 in the year 2010. It increased in value at a rate of 4% per year. Find the value of the art at the end of the year 2015.
Sol: To find the value of the art at the end of the year 2015, we use the compound interest formula:
- Principal () = $5,000
- Rate () = 4%
- Time () = 2015 - 2010 = 5 years
≈1.2167
Multiply by the principal:
So, the value of the art at the end of the year 2015 is approximately $6,083.50.
|
81 videos|452 docs|31 tests
|
FAQs on Comparing Quantities Chapter Notes - Mathematics (Maths) Class 8
| 1. What are ratios and how are they used in comparing quantities? |  |
| 2. How can I calculate a discount on a product? |  |
| 3. What is the difference between sales tax and value-added tax (VAT)? |  |
| 4. How is compound interest calculated? |  |
| 5. What are the applications of the compound interest formula? |  |