Evaluation Chapter Notes | Artificial Intelligence for Class 10 PDF Download
| Table of contents |

|
| What is Evaluation? |

|
| Evaluation Terminologies |

|
| Confusion Matrix |

|
| Precision |

|
| F1 Score |

|
| Which Metric is Important? |

|
What is Evaluation?
Evaluation is a process that critically examines a program. It involves collecting and analyzing information about a program’s activities, characteristics, and outcomes. Its purpose is to make judgments about a program, to improve its effectiveness, and/or to inform programming decisions.
Let me explain this to you:
Evaluation is basically to check the performance of your AI model. This is done by mainly two things: “Prediction” & “Reality“. Evaluation is done by:
- First, search for some testing data with the resulted outcome that is 100% true.
- Then, feed that testing data to the AI model while you have the correct outcome with yourself, which is termed as “Reality.”
- When you get the predicted outcome from the AI model, called “Prediction,” compare it with the actual outcome, that is, “Reality.”
You can do this to:
- Improve the efficiency and performance of your AI model.
- Identify and correct mistakes.

Prediction and Reality
- Try not to use the dataset that has been used in the process of data acquisition or the training data in evaluation.
- This is because your model will simply remember the whole training set and will therefore always predict the correct label for any point in the training set. This is known as overfitting.
Evaluation Terminologies
There are various terminologies that come in when we work on evaluating our model. Let’s explore them with an example of the Football scenario
The Scenario
- Imagine you have developed an AI-based prediction model designed to identify a football (soccer ball). The objective of the model is to predict whether the given/shown figure is a football. To understand the efficiency of this model, we need to check if the predictions it makes are correct or not. Thus, there exist two conditions that we need to consider: Prediction and Reality.
- Prediction: The output given by the machine.
- Reality: The actual scenario about the figure shown when the prediction has been made.
- Now, let's look at various combinations that we can have with these two conditions:
- True Positive (TP): The model predicts the figure as a football, and it is indeed a football.
- True Negative (TN): The model predicts the figure as not a football, and it is indeed not a football.
- False Positive (FP): The model predicts the figure as a football, but it is not a football.
- False Negative (FN): The model predicts the figure as not a football, but it is indeed a football.
By analyzing these combinations, we can evaluate the performance and efficiency of the AI model. The goal is to maximize the number of True Positives and True Negatives while minimizing the number of False Positives and False Negatives.
1. Possibility
2. Case
3. Possible action
4. Last case
Confusion Matrix
The comparison between the results of Prediction and Reality is known as the Confusion Matrix.
The confusion matrix helps us interpret the prediction results. It is not an evaluation metric itself but serves as a record to aid in evaluation. Let’s review the four conditions related to the football example once more.
Confusion Matrix table

Parameters to Evaluate a Model
Now let us go through all the possible combinations of “Prediction” and “Reality” & let us see how we can use these conditions to evaluate the model.
Accuracy
Definition: Accuracy is the percentage of “correct predictions out of all observations.” A prediction is considered correct if it aligns with the reality.
In this context, there are two scenarios where the Prediction matches the Reality:
Accuracy Formula
- Accuracy Word formula:

- Accuracy Formula:

Here, total observations cover all the possible cases of prediction that can be True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN).
Example: Let’s revisit the Football example.
Assume the model always predicts that there is no football. In reality, there is a 2% chance of encountering a football. In this scenario, the model will be correct 98% of the time when it predicts no football. However, it will be incorrect in the 2% of cases where a football is actually present, as it incorrectly predicts no football.
Here:
Conclusion

Precision
Definition: The percentage of "true positive cases" out of all cases where the prediction is positive. This metric considers both True Positives and False Positives. It measures how well the model identifies positive cases among all cases it predicts as positive.
In other words, it evaluates the proportion of correctly identified positive instances compared to all instances the model predicted as positive.
Precision Formula
- Precision Word Formula:

- Precision Formula:

Definition: Precision is the percentage of “true positive cases” out of all cases where the prediction is positive. It considers both True Positives and False Positives.
In the football example, if the model always predicts the presence of a football, regardless of reality, all positive predictions are evaluated, including:
- True Positive (Prediction = Yes and Reality = Yes)
- False Positive (Prediction = Yes and Reality = No)
Just like the story of the boy who falsely cried out about wolves and was ignored when real wolves arrived, if the precision is low (indicating more false positives), it could lead to complacency. Players might start ignoring the predictions, thinking they're mostly false, and thus fail to check for the ball when it’s actually there.
Example:
Recall
Definition: Recall, also known as Sensitivity or True Positive Rate, is the fraction of actual positive cases that are correctly identified by the model.
In the football example, recall focuses on the true cases where a football was actually present, examining how well the model detected it. It takes into account:
- True Positives (TP): Cases where the model correctly identified the presence of a football.
- False Negatives (FN): Cases where a football was present, but the model failed to detect it.

Recall Formula
- Recall Word Formula:

- Recall Formula:

In both Precision and Recall, the numerator is the same: True Positives. However, the denominators differ: Precision includes False Positives, while Recall includes False Negatives.
F1 Score
Definition: The F1 Score measures the balance between precision and recall. It is used when there is no clear preference for one metric over the other, providing a way to seek a balance between them.
F1 Score Formula
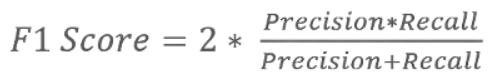
Which Metric is Important?
Choosing between Precision and Recall depends on the specific context and the costs associated with False Positives and False Negatives:
- Forest Fire Detection: Here, a False Negative (failing to detect a fire when there is one) is critical because it could lead to devastating consequences, like the forest burning down. Therefore, Recall (which emphasizes detecting all positive cases) is crucial in this scenario.
- Viral Outbreak Prediction: A False Negative here (not identifying an outbreak when it occurs) can lead to widespread infection and severe public health issues. Hence, Recall is again more important.
- Mining: If a model predicts the presence of treasure (a False Positive) but there's none, it could result in unnecessary and costly digging. In this case, Precision (which focuses on avoiding false alarms) is more valuable.
- Spam Email Classification: If a model incorrectly labels a legitimate email as spam (a False Positive), it could lead to missing important messages. Therefore, Precision is critical in this scenario as well.
Cases of High FN Cost:
- Forest Fire
- Viral
Cases of High FP Cost:
- Spam
- Mining
Both the parameters are important
- High Precision:

- High Recall:

To sum up, if you want to assess your model’s performance comprehensively, both Precision and Recall are crucial metrics.
- High Precision might come at the cost of Low Recall, and vice versa.
- The F1 Score is a metric that balances both Precision and Recall, providing a single score to evaluate model performance.
- An ideal scenario would be where both Precision and Recall are 100%, leading to an F1 Score of 1 (or 100%).
Both Precision and Recall range from 0 to 1, and so does the F1 Score, with 1 representing the perfect performance.
F1 Score Table
Let us explore the variations we can have in the F1 Score:
|
41 videos|35 docs|6 tests
|
FAQs on Evaluation Chapter Notes - Artificial Intelligence for Class 10
| 1. What is the purpose of a confusion matrix in evaluation? |  |
| 2. How is the accuracy of a model calculated using a confusion matrix? |  |
| 3. What is precision and recall in the context of evaluation terminologies? |  |
| 4. How can one interpret the F1 score when evaluating a model's performance? |  |
| 5. Why is it important to consider both false positives and false negatives in evaluation metrics? |  |

|
Explore Courses for Class 10 exam
|

|

























