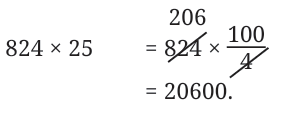Large Numbers Around Us Class 7 Notes Maths Chapter 1 Free PDF
A Lakh Varieties!
 Have you ever thought about how many grains of rice are in a single bag, or how many stars twinkle in the night sky? Numbers are everywhere, helping us count, measure, and understand the world around us. Sometimes, these numbers are small, like the number of fingers on your hand. But often, especially when we talk about populations, distances between cities, or even the variety of life on Earth, the numbers become very, very large!
Have you ever thought about how many grains of rice are in a single bag, or how many stars twinkle in the night sky? Numbers are everywhere, helping us count, measure, and understand the world around us. Sometimes, these numbers are small, like the number of fingers on your hand. But often, especially when we talk about populations, distances between cities, or even the variety of life on Earth, the numbers become very, very large! Eshwarappa hearing a conversation That sounds like a huge number. Eshwarappa Eshwarappa shared this incident with his daughter Roxie and son Estu . They wonder,
Eshwarappa hearing a conversation That sounds like a huge number. Eshwarappa Eshwarappa shared this incident with his daughter Roxie and son Estu . They wonder, “Can a person taste all 1 lakh rice varieties in their lifetime?”
Let's Calculate!

There are 365 days in a year.
So if someone lives for 100 years, the number of days is:
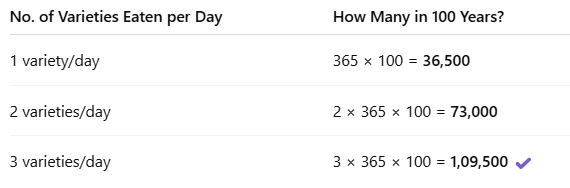
So, if someone eats 3 different types of rice every single day for 100 years, they can taste all 1 lakh rice varieties!
This story from your textbook introduces us to the fascinating world of large numbers. It makes us question: How big is a lakh? How do we even write or say such big numbers?
Getting a Feel for Large Numbers
Sometimes, we hear big numbers like 180 metres or 450 metres—but it's hard to imagine how tall that really is. So we compare it to something we know.
Let’s Look at Somu’s Building
Somu is 1 metre tall.
Each floor is about 4 times his height.
So, 1 floor = 4 metres.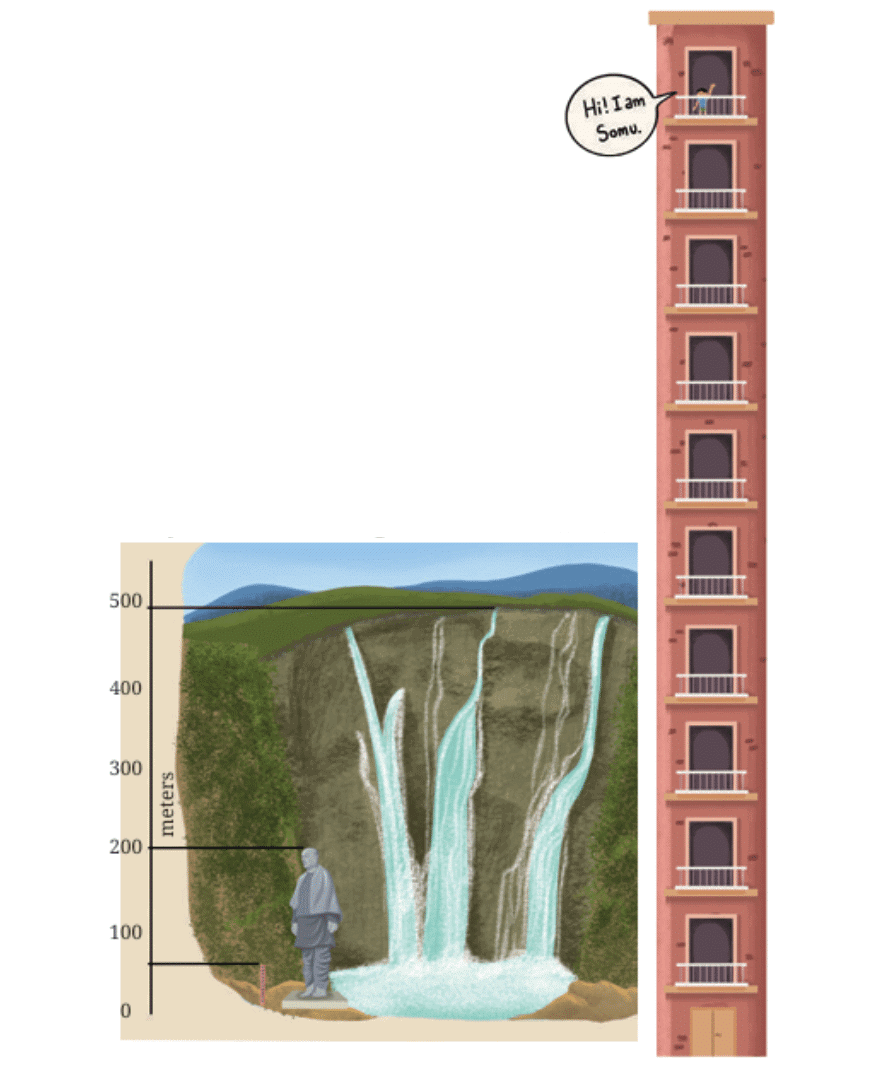
There are 10 floors, so the total height of the building is:
metres
Q1: Which is taller — The Statue of Unity or Somu’s building? How much taller?
Statue of Unity = 180 metres
Somu’s building = 40 metres
metres taller
Answer: The Statue of Unity is taller by 140 metres.
Q2: How much taller is the Kunchikal waterfall than Somu's building?
Waterfall height = 450 metres
Building height = 40 metres
metres taller
Answer: The waterfall is 410 metres taller than Somu’s building.
Q3: How many floors should Somu’s building have to be as tall as the waterfall?
Waterfall = 450 metres
1 floor = 4 metres
We can't have half a floor in reality, so we round up to 113.
Answer: Somu’s building should have 113 floors to be as tall as the waterfall!
Is One Lakh a Very Large Number?
This is actually a very interesting question because...
Sometimes 1 lakh feels very big and sometimes it feels small, depending on what we are talking about.
Let’s see why:
Roxie gives three examples to show how huge one lakh can feel:
 1 Lakh Varieties of Rice
1 Lakh Varieties of RiceImagine tasting a new type of rice every day.
It would take 274 years to try them all!
We live only about 70–80 years. So, we’ll never finish them!
Living for 1 Lakh Days
One year has 365 days.
1,00,000 ÷ 365 ≈ 274 years!
That’s like living three lifetimes. So yes, it’s big.
1 Lakh People Standing in a Line
If each person takes about 0.38 meters of space, then:
1,00,000 people = 38 km long line.
That’s like a line from one city to another!
Estu gives a different view. He shows how small 1 lakh can feel:
Stadium Seats
The cricket stadium in Ahmedabad holds more than 1 lakh people.
They all fit in one place — that feels not so big, right?
Hair on a Human Head
An average person has 80,000 to 1,20,000 hairs.
That means 1 lakh hairs fit on your head!
So, in a tiny space, you can already have 1 lakh things.
Fish Eggs
Some fish can lay 1 lakh eggs at once!
Even 10 lakh (a million) in some species!
That makes 1 lakh seem small in nature.
Q: So, is 1 lakh big or small?
Ans: It depends on what you're comparing it with.
If you're saving ₹1 lakh, it feels like a lot of money.
But if a government spends ₹1 lakh on a city, it’s very little.
If you’re counting people or things in small spaces, 1 lakh may not feel big.
But if you want to do something 1 lakh times, it’s a huge effort.
Reading and Writing Large Numbers
The Indian Place Value System
In the Indian system, numbers are grouped into hundreds, thousands, lakhs, crores, and so on. Here’s a breakdown:
- Units: The first three digits from the right are the units, tens, and hundreds.
- Thousands: The next two digits are the thousands.
- Lakhs: The next two digits are the lakhs.
- Crores: The digits after lakhs are the crores.
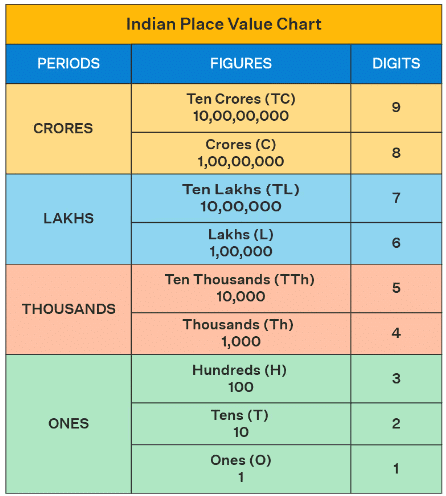 Indian Place Value Chart
Indian Place Value Chart
Comma Rules:
The first comma comes after 3 digits from the right (thousands group).
Next commas come after 2 digits each.
Example:
12,78,830 is grouped as 12 (lakhs), 78 (thousands), 830 (hundreds & below)
Q: Write these in words:
(a) 3,00,600
Ans: Three lakh six hundred
(b) 5,04,085
Ans: Five lakh four thousand eighty-five
(c) 27,30,000
Ans: Twenty-seven lakh thirty thousand
(d) 70,53,138
Ans: Seventy lakh fifty-three thousand one hundred thirty-eight
Writing Number Names as Numbers
Now let’s go the other way — you are given the number in words, and you need to write it in figures (numbers).
Q: Write the numbers
(a) One lakh twenty-three thousand four hundred and fifty-six
Ans: 1,23,456
(b) Four lakh seven thousand seven hundred and four
Ans: 4,07,704
(c) Fifty lakhs five thousand and fifty
Ans: 50,05,050
(d) Ten lakhs two hundred and thirty-five
Ans: 10,00,235
The Land of Tens
- Thoughtful Thousands (+1000 button): To make 3,000, you press it 3 times. To make 10,000, you press it 10 times. To make one lakh (1,00,000), you need to press it 100 times (since 1 lakh = 100 thousand).

- Tedious Tens (+10 button): To make 500, you press it 50 times (50 x 10 = 500). To make 1,000, you press it 100 times (100 x 10 = 1000). To make one lakh (1,00,000), you need a whopping 10,000 presses (10,000 x 10 = 1,00,000)!

- Handy Hundreds (+100 button): To make 3,700, you press it 37 times (37 x 100 = 3700). To make 10,000, you press it 100 times (100 x 100 = 10,000). To make one lakh (1,00,000), you press it 1,000 times (1,000 x 100 = 1,00,000).

What is Place Value?
Place value defines the value of each digit in a number based on its position. Each position, or "place," in a number has a unique value that helps determine the overall number.
Example 1: What are the place values of each digit in the number 92,735?
Ans:
- 5 is Ones
- 3 is Tens
- 7 is Hundreds
- 2 is Thousands
- 9 is Ten thousands
The diagram below illustrates the above example in more detail.

 I am Creative ChittiChitti shows that numbers can be made in many ways. For example, 5072 could be:
I am Creative ChittiChitti shows that numbers can be made in many ways. For example, 5072 could be:- (50 x 100) + (7 x 10) + (2 x 1) = 5000 + 70 + 2 = 5072
- (3 x 1000) + (20 x 100) + (72 x 1) = 3000 + 2000 + 72 = 5072
- Another way: (4 x 1000) + (10 x 100) + (6 x 10) + (12 x 1) = 4000 + 1000 + 60 + 12 = 5072
- +1000 button: 5 times (for 5000)
- +100 button: 0 times (for 0 hundreds)
- +10 button: 7 times (for 70)
- +1 button: 2 times (for 2)
Expanded Form: When we write a number in expanded form, we break it down to show the value of each digit. It's like stretching the number out to see each part clearly.
Example 2: Write in expanded form: 4,582
Sol: Let's expand 4,582:
- Thousands place: The digit 4 is in the thousands place, so its value is 4,000.
- Hundreds place: The digit 5 is in the hundreds place, so its value is 500.
- Tens place: The digit 8 is in the tens place, so its value is 80.
- Ones place: The digit 2 is in the ones place, so its value is 2.
Putting it all together:
4,582 = 4,000 + 500 + 80 + 2
Of Crores and Crores!
As numbers get bigger, it becomes difficult to read and understand them unless they are written properly with commas. To help us, two main systems are used around the world:
The Indian Number System
The International Number System (also called the American System)
- 1 Crore = 100 Lakhs
- 1 Crore = 1,00,00,000 (That's a 1 followed by seven zeros!)
- 1 Arab = 100 Crores
- 1 Arab = 1,00,00,00,000 (A 1 followed by nine zeros!)
International System of Writing Numbers
- The number 100000 is read as one hundred thousand or 1 lakh. It is a 6-digit numeral.
- In the International System, the number 10 lakh or ten hundred thousand, that is, a thousand thousand, is called a million.
- It is written as under:
 Instead of lakhs, crores, etc. as periods, we use millions, billions, etc.
Instead of lakhs, crores, etc. as periods, we use millions, billions, etc.
- Let us write the smallest 8-digit number in the two systems of numerations.

- The International place value chart is given below.

- The chart can be expanded to include more than nine places.
- The section just before the millions is known as the billions section.
- Next, we have the trillions section.
- The places before the hundred billions are referred to as:
- trillions place
- ten trillions place
- hundred trillions place - When we compare the two systems of counting, we can see the following connections.

- Note that in the Indian system, starting from the right after the first period of 3 digits all other periods are of 2 digits but in the International system, each period consists of three digits.
- We place a comma or leave space after every 3 digits.
- The abacus shows the number six million eight hundred forty-nine thousand two hundred forty.
- To make the task of reading and writing such large numbers easy, start counting digits from the right by threes and leave some space or put a comma after every three digits as shown below.


Number Names – Indian vs. American
Let’s take an example number:
→ 9876501234
In the Indian system, we place commas like this:
9,87,65,01,234
We read it as:
9 arab 87 crore 65 lakh 1 thousand 234
or
987 crore 65 lakh 1 thousand 234
In the American system, commas look like this:
9,876,501,234
We read it as:
9 billion 876 million 501 thousand 234
Understanding Zeros in Large Numbers
1 thousand = 1,000 → 3 zeros
1 lakh = 1,00,000 → 5 zeros
1 crore = 1,00,00,000 → 7 zeros
1 arab = 1,00,00,00,000 → 9 zeros
Now let's answer these questions:
Q: How many zeros in a thousand lakh?
1 lakh = 1,00,000
1,000 × 1,00,000 = 1,00,00,00,000 → 8 zeros
But let's calculate more carefully:
(which is actually 10 crores)
So the number has 8 zeros.
Q: How many zeros in a hundred thousand?
1 thousand = 1,000
100 × 1,000 = 1,00,000 → 5 zeros
So Ans: 5 zeros

Exact and Approximate Values
 Read the image above. Does this mean exactly 100,000 people walked through the gates?
Read the image above. Does this mean exactly 100,000 people walked through the gates? Probably not! It's likely an approximation or an estimate. The actual number might have been 98,543 or maybe 101,210.
For a headline, saying "about 1 lakh" gives a good enough idea of the crowd size without needing the precise count.
Why do we use approximate numbers?
Example:
The exact population of Chintamani town is 76,068.
But saying “about 75,000 people live there” gives a quick idea without needing to know the exact count.

Two Common Ways of Rounding:
1. Rounding Up:
When we increase the number to a higher, easier number.
Example: A school has 732 people. The principal may round it up and order 750 sweets.
2. Rounding Down:
When we reduce the number a little to make it simpler.
Example: An item costs ₹470, but the shopkeeper might say it’s around ₹450.
Let's Summarise:

Nearest Neighbours
Rule: If the digit to the right is 5 or greater, round up the digit in the target place value. If the digit to the right is 4 or less, keep the digit in the target place value the same. All digits to the right of the target place value become zeros.
- Nearest Thousand:
Look at the hundreds digit (1).
Since 1 < 5, keep the thousands digit (5) the same.
6,72,85,000 - Nearest Ten Thousand:
Look at the thousands digit (5).
Since 5 ≥ 5, round up the ten thousands digit (8) to 9.
6,72,90,000 - Nearest Lakh:
Look at the ten thousands digit (8).
Since 8 ≥ 5, round up the lakhs digit (2) to 3.
6,73,00,000 - Nearest Ten Lakh:
Look at the lakhs digit (2).
Since 2 < 5, keep the ten lakhs digit (7) the same.
6,70,00,000 - Nearest Crore:
Look at the ten lakhs digit (7).
Since 7 ≥ 5, round up the crores digit (6) to 7.
7,00,00,000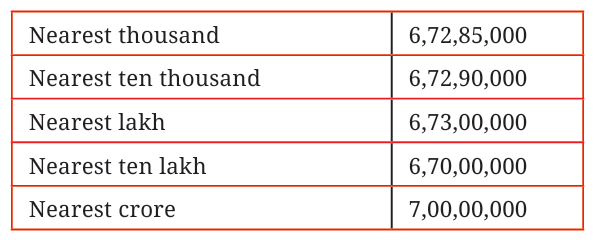
Patterns in Products
Instead of multiplying directly by numbers like 5, 25, or 50, Roxie and Estu uses a shortcut based on how those numbers relate to 10, 100, or 1000.
These shortcuts are possible because:
5 = 10 ÷ 2
25 = 100 ÷ 4
50 = 100 ÷ 2
125 = 1000 ÷ 8
So, multiplying a number by 5 is the same as:
Dividing the number by 2 and then multiplying by 10
→ a × 5 = (a ÷ 2) × 10
And multiplying a number by 25 is the same as:
Dividing the number by 4 and then multiplying by 100
→ a × 25 = (a ÷ 4) × 100
These are based on properties of multiplication and division:
Multiplication is associative and distributive
You can rearrange factors in multiplication for easier calculation
For example:
a × 5 = a × (10 ÷ 2) = (a ÷ 2) × 10
This works because multiplication and division are inverse operations that can be grouped like this for easier solving.
Example 1: 116 × 5
Instead of directly multiplying 116 × 5, Roxie breaks it into:
116 × 5 = (116 ÷ 2) × 10
Why does this work?
Because 5 = 10 ÷ 2, so multiplying by 5 is the same as dividing the number by 2 and then multiplying the result by 10.
So,
116 ÷ 2 = 58
Then, 58 × 10 = 580
Example 2: 824 × 25
Estu applies a similar shortcut:
824 × 25 = (824 ÷ 4) × 100
Why?
Because 25 = 100 ÷ 4, so multiplying by 25 is like dividing by 4 and then multiplying the result by 100.
So,
824 ÷ 4 = 206
Then, 206 × 100 = 20600
Fascinating Facts about Large Numbers
This lesson uses real-world facts involving huge numbers to show how multiplication and divisionhelp us understand large quantities — like distances, weights, populations, and more.
1. Using Multiplication to Discover Big Facts


2. Using Division to Break Down Big Facts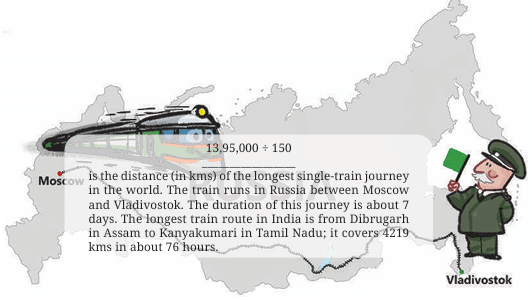

Did You Ever Wonder....?
Estu's Question:
Can the entire population of Mumbai fit into 1 lakh buses?
Step 1: Understand the Numbers
1 lakh buses = 1,00,000 buses
Each bus holds = 50 people
So, total people in 1 lakh buses =
1,00,000 × 50 = 50,00,000= 50 lakh people
Step 2: Compare with Mumbai’s Population
Population of Mumbai = 1 crore 24 lakh = 1,24,00,000 people
People buses can carry = 50 lakh
So, can everyone fit into the buses?
No! Because 1 crore 24 lakh is more than double 50 lakh.
Conclusion: The whole population of Mumbai cannot fit in 1 lakh buses.
Now think about the Titanic Ship:
Can the population of Mumbai fit into 5000 Titanic-like ships?
Step 1: How many people fit in 1 ship?
Each Titanic can carry = 2,500 people
So, 5000 ships can carry =
5000 × 2500 = 1,25,00,000 = 1 crore 25 lakh people
Step 2: Compare again
Mumbai's population = 1 crore 24 lakh
Space on ships = 1 crore 25 lakh
Yes! The population of Mumbai can fit into 5000 Titanic-like ships.
Solved Examples
Ans: Seventy lakh fifty-three thousand one hundred thirty-eight.
Ans: 50,05,050
Example 3: Compare 500 lakhs and 5 million. Use '<', '>', or '='.
Ans: 500 lakhs = 500 x 1,00,000 = 5,00,00,000
5 million = 5 x 1,000,000 = 5,000,000
Since 5,00,00,000 is much larger than 5,000,000,
500 lakhs > 5 million
Example 4: Using Systematic Sippy's method (fewest clicks), how would you make the number 3,67,813? Write the expression.
Ans: +1,00,000 button: 3 times (3 lakhs)
+10,000 button: 6 times (6 ten thousands)
+1,000 button: 7 times (7 thousands)
+100 button: 8 times (8 hundreds)
+10 button: 1 time (1 ten)
+1 button: 3 times (3 ones) Total clicks = 3 + 6 + 7 + 8 + 1 + 3 = 28 clicks.
Expression: (3 x 1,00,000) + (6 x 10,000) + (7 x 1,000) + (8 x 100) + (1 x 10) + (3 x 1)
Ans: Look at the digit in the thousands place: 9.
Since 9 ≥ 5, we round up the digit in the ten thousands place (6) to 7.
Rounded number: 3,87,70,000
FAQs on Large Numbers Around Us Class 7 Notes Maths Chapter 1 Free PDF
| 1. What is a lakh and how is it represented in numbers? |  |
| 2. How do the Indian and International numbering systems differ? |  |
| 3. What is place value and how does it apply to large numbers? |  |
| 4. What are crores and how do they relate to lakhs? |  |
| 5. How can estimation and rounding help when dealing with large numbers? |  |