Number Play Class 7 Notes Maths Chapter 6 Free PDF
| Table of contents |

|
| Numbers Tell us Things |

|
| Picking Parity |

|
| Some Explorations in Grids |

|
| Nature’s Favourite Sequence: The Virahāṅka- Fibonacci Numbers! |

|
| Digits in Disguise |

|
Numbers Tell us Things
Numbers aren't just for counting; they can represent relationships and follow specific rules.
Imagine a group of children standing in a line. Each child is given a number, but the number they say does not match the order in which they are standing.
Let’s understand this using both pictures shown.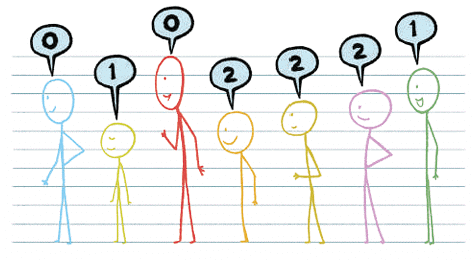 Children are standing in a straight line and saying numbers: (0,1,0,2,2,2,1)
Children are standing in a straight line and saying numbers: (0,1,0,2,2,2,1)
So the pattern seems unclear for now. But now, let’s look at what happens in the second image.
 Now the same children are in a new order, and they say: (0,0, 1, 2, 2, 5, 6)
Now the same children are in a new order, and they say: (0,0, 1, 2, 2, 5, 6)
If you observe carefully, this isn't just random! Something is happening based on their positions.
What Do These Numbers Actually Mean?
Guess 1: The numbers show how many people are in front who are taller.
Imagine the height of each child is fixed.
Let’s say the red child is tallest. So in the first arrangement, the children call out the number of children taller than them in front of them.
Guess 2: The numbers are showing how many children are taller or shorter around them or how many children came before them in line.
So the number each child says seems to reflect how many children are taller and ahead of them in line.
It’s like each child is counting how many kids ahead of them are taller.

Picking Parity
Parity refers to the property of a number being either even or odd.
This section explores the rules and patterns related to parity.
Kishor's Puzzle:
Kishor has number cards (1, 3, 5, 7, 9, 11, 13) and 5 empty boxes. He needs to place exactly one card in each box such that the numbers sum to 30. Can he do it?
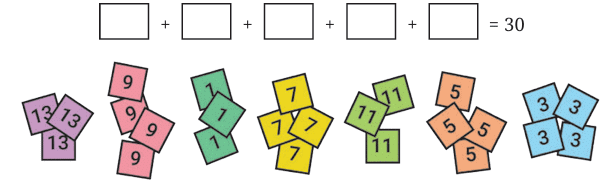
Let's investigate the properties of even and odd numbers to solve this.
Properties of Even and Odd Numbers:
Even numbers: Can be grouped in pairs with no leftovers. Example: 2, 4, 6, 8, 10...
 No pair is left
No pair is leftOdd numbers: Always leave one unpaired object. Example: 1, 3, 5, 7, 9...
What happens when you add two odd numbers? One unpaired left
One unpaired leftThe sum of two odd numbers can always be arranged in pairs, meaning the sum is even.
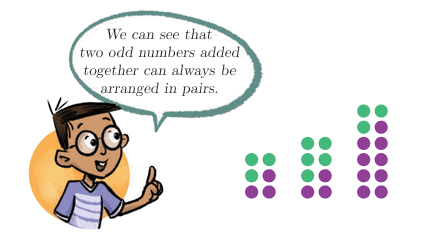
What about adding three odd numbers? Can the sum be arranged in pairs?
No. The sum of three odd numbers is odd.
The Puzzle:
Kishor has some number cards. He needs to place 5 cards in boxes so that their total equals 30.
The number cards are:
13, 9, 7, 11, 5, 3
All are odd numbers.
But here’s the question: Can the sum of 5 odd numbers be 30 (an even number)?
Let’s try:
Add 3 + 5 + 7 + 9 + 11 = 35 ❌
Try different combinations – Still doesn’t give you 30!
Let’s use parity logic.
When you add even numbers, the result is always even.
When you add two odd numbers, the result is even.
BUT, when you add an odd number of odd numbers (like 3, 5, or 7 odd numbers), the result is always odd.
So: ✅ 2 odd numbers → even
✅ 4 odd numbers → even
❌ 5 odd numbers → odd
So it's impossible to make 30 (which is even) by adding 5 odd numbers. That’s the trick of parity!
So the answer of Kishore's Puzzle is no.
Real-Life Example:
Martin and Maria are siblings born one year apart. If their total age is 112, is that possible?
Try:
Martin = 55, Maria = 56 → 55 + 56 = 111 (odd)
Martin = 56, Maria = 57 → 113 (odd)
You can try any two consecutive numbers, and they always add up to an odd number. So, 112 is not possible.
Why?
Because one of them will be odd and the other even → odd + even = odd.
Small Squares in Grids:
A 3 × 3 grid has 9 squares (odd).
A 3 × 4 grid has 12 squares (even).

Can you tell the parity of the total squares just from the dimensions?
Rule: The product (total squares) is odd only if both dimensions are odd.
Odd × Odd = Odd
Odd × Even = Even
Even × Odd = Even
Even × Even = Even
Parity of Expressions:
Consider 3n + 4. Its parity depends on n:
If n is odd, 3n is odd, 3n + 4 (odd + even) is odd.
If n is even, 3n is even, 3n + 4 (even + even) is even.

Expressions that are always even: Any expression where the result must have a factor of 2. Examples: 2n, 100p, 48w - 2, 6k + 2, n + n.
Expressions that are always odd: An even expression plus or minus 1. Examples: 2n + 1, 2n - 1.
Finding the nth Even and Odd Number:
The nth even number is given by the formula 2n.
Example: The 100th even number is 2 × 100 = 200.
The nth odd number is one less than the nth even number. The formula is 2n - 1.
Example: The 100th odd number is (2 × 100) - 1 = 200 - 1 = 199.
Some Explorations in Grids
Let's explore number patterns within grids.
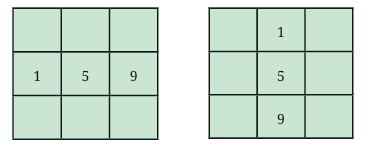
The 3x3 Sum Grid Puzzle:
Observe the 3x3 grid below. 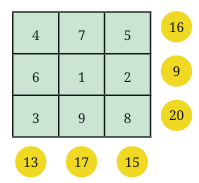 It's filled with numbers 1 to 9, with no repeats. The circled numbers outside represent the sum of the numbers in the corresponding row or column.
It's filled with numbers 1 to 9, with no repeats. The circled numbers outside represent the sum of the numbers in the corresponding row or column.
Can you verify the row and column sums?
Challenge Grids:
Fill the grids below using numbers 1-9 without repetition, ensuring the row and column sums match the circled numbers.
Grid 1: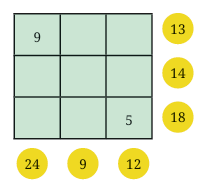 Ans:
Ans: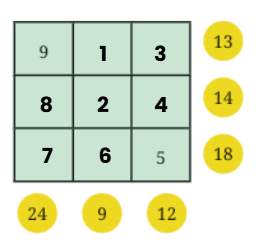
Grid 2: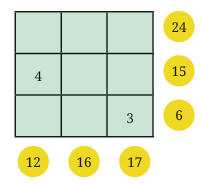
Ans: 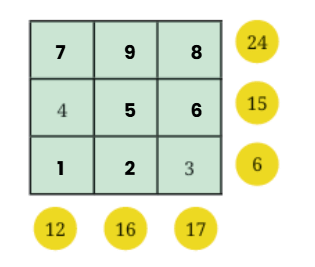
Impossible Grid?
Consider this grid setup:

Is it possible to find a solution? Why or why not?
Reasoning: The smallest possible sum for a row/column using three distinct numbers from 1-9 is 1 + 2 + 3 = 6. The largest possible sum is 7 + 8 + 9 = 24. Any circled sum must be between 6 and 24, inclusive. In the grid above, the first column requires a sum of 5, which is impossible. Therefore, this grid has no solution.
Total Sum Check:
What is the sum of all numbers from 1 to 9? (1 + 2 + ... + 9 = 45).
What is the sum of all the row sums (or column sums) in a completed 3x3 grid puzzle?
It must also be 45, as each number in the grid is counted exactly once in the row sums and exactly once in the column sums.
What is a Magic Square?
A magic square is a special grid of numbers where:
The sum of numbers in every row, every column, and both diagonals is the same.
This common total is called the magic sum.
In a 3 × 3 magic square, we use numbers 1 to 9, without repetition.
Look at this 3 × 3 grid from the image: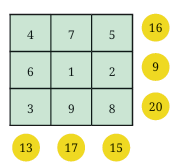
But here’s the catch—this grid is not a magic square, because:
Row sums: 16, 9, and 20 (not equal)
Column sums: 4+6+3=13, 7+1+9=17, 5+2+8=15 (also not equal)
Diagonals: Not the same sum either
So, this is just a filled 3×3 grid, not a magic square.
So, what makes it a real magic square?
Let’s take the correct magic square example:
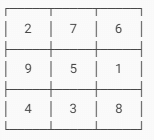
Now, check the magic:
Each row adds to 15
2 + 7 + 6 = 15
9 + 5 + 1 = 15
4 + 3 + 8 = 15
Each column adds to 15
2 + 9 + 4 = 15
7 + 5 + 3 = 15
6 + 1 + 8 = 15
Both diagonals add to 15
2 + 5 + 8 = 15
6 + 5 + 4 = 15
This is a true magic square with magic sum = 15.
Why is the magic sum always 15 in a 3x3 magic square?
The total sum of all numbers from 1 to 9 is:
1 + 2 + 3 + ... + 9 = 45
Now, this total of 45 is split evenly across 3 rows (or 3 columns), so:
45 ÷ 3 = 15
That’s why the magic sum for every row/column/diagonal must be 15.
Can the magic sum be any number?
No, not when using 1 to 9 without repetition. The magic sum is fixed because:
You're using the same numbers (1 to 9).
The total is always 45.
So, magic sum = total ÷ number of rows = 45 ÷ 3 = 15
If you use a different set of numbers (like 2 to 10), then the total and magic sum will change.
Let us focus, for the moment, only on the row sums. We have seen that in a 3 × 3 grid with numbers 1 – 9, the total of row sums will always be 45. Since in a magic square the row sums are all equal, and they add up to 45, they have to be 15 each. Thus, we have the following observation.
Observation 1:
All rows, columns, and diagonals must add up to 15.
Can 9 be at the centre?
Let’s try putting 9 in the centre:
Now imagine one of the rows has 8 and 9.
So:
8 + 9 + ? = 15
17 + ? = 15
That’s impossible! 17 is already more than 15. So no matter what the third number is, the total will not be 15.
So, 9 cannot be at the centre.
Can 1 be at the centre?
Now try 1 in the centre. Imagine another number in the same row: 2.
1 + 2 + ? = 15
3 + ? = 15
⇒ ? = 12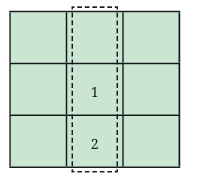
But we are only allowed to use numbers from 1 to 9, and 12 is not allowed.
So, 1 cannot be at the centre either.
Try All Numbers from 1 to 9
If you keep trying this way for every number from 1 to 9, you’ll find:
✅ Only 5 can be at the centre, because only with 5 in the centre, we can find four different combinations of two numbers that add with 5 to make 15:
5 + 1 + 9 = 15
5 + 2 + 8 = 15
5 + 3 + 7 = 15
5 + 4 + 6 = 15
Observation 2:
The number 5 must be at the center of the magic square.
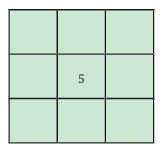
Why? Because it’s the middle value of numbers 1–9 and balances the other values.
What About Numbers 1 and 9?
Now let’s think: where should the smallest number (1) and the largest number (9) go?
They cannot go in the centre (we just saw why).
So, they must go in one of the outer positions — either in a corner or on the sides.
Let’s check if 1 can be placed in a corner.
We need to find combinations like:
Some possible ones are:
1 + 5 + 9 = 15
1 + 6 + 8 = 15
That’s two valid combinations.
Now try 9 in a corner.
Possible combinations:
9 + 1 + 5 = 15
9 + 2 + 4 = 15
Again, two valid combinations.
Observation 3:
Numbers 1 and 9 cannot be placed in the corners. If you place them there, you cannot find enough combinations to make 15.
So, they must go in the middle positions on the boundary (not in the corners or center).
How to Start Filling the Magic Square
Let’s say we place 1, 5, and 9 in one row or column like this:
That already adds up to 15. Now we can fill the other positions in a way that each row, column, and diagonal still adds up to 15.
Try completing the square from here by using:
Remaining numbers: 2, 3, 4, 6, 7, 8
Make sure each number is used only once
Check each row, column, and diagonal
A Classic 3 × 3 Magic Square:
Rows: 2+7+6 = 15, 9+5+1 = 15, 4+3+8 = 15
Columns: 2+9+4 = 15, 7+5+3 = 15, 6+1+8 = 15
Diagonals: 2+5+8 = 15, 6+5+4 = 15
✅ Every direction adds up to the magic sum of 15!
Generalising a 3 × 3 Magic Square
When we generalise something in Maths, we try to find a pattern or rule that works for all similar cases, not just one example.
In this case, we want to look at how the numbers in a 3 × 3 magic square are related to the centre number, and then write that using algebra.
Let’s say we are working with a 3 × 3 magic square made using consecutive numbers, like 1 to 9. Here's one example: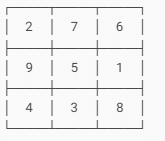
The middle number is 5, and the magic sum is 15.
Now let’s call the middle number m. So in this example, m = 5.
We now want to describe every other number in terms of how much more or less it is than m.
Let’s place m in the centre of the grid:
Now let’s figure out how the other numbers relate to m. We’ll use + or − to show how far they are from m.
In a typical 3 × 3 magic square, if m is the centre, then the numbers around it are arranged as follows: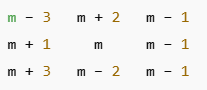
But we need to use a pattern that always gives us the magic square.
Here is the correct general form of a 3 × 3 magic square using m as the centre: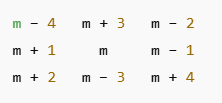
When we generalise the magic square, we find a formula or pattern for where each number goes in relation to the centre number m.
The First-ever 4 × 4 Magic Square
This is a wonderful example of a 4 × 4 magic square from ancient India, called the Chautīśā Yantra, found in the Parshvanath Jain temple in Khajuraho. Let’s explore and understand this amazing pattern! The first ever recorded 4 × 4 magic square, the Chautīsā Yantra, at Khajuraho, India
The first ever recorded 4 × 4 magic square, the Chautīsā Yantra, at Khajuraho, India
A magic square is a grid of numbers where:
Each row, column, and both diagonals add up to the same total.
In this case, it's a 4 × 4 grid, meaning it has 4 rows and 4 columns.
The sum of each row/column/diagonal is 34.
That's why it’s called the Chautīśā Yantra — “Chautīśā” means 34 in Hindi.
Let’s check some sums of the given grid:
Row 1: 7 + 12 + 1 + 14 = 34
Column 1: 7 + 2 + 16 + 9 = 34
Diagonal (top-left to bottom-right): 7 + 13 + 10 + 4 = 34
Diagonal (top-right to bottom-left): 14 + 8 + 3 + 9 = 34
✅ Every row, column, and diagonal gives the same magic sum = 34.
Can We Find Other Patterns That Also Add Up to 34?
Yes! The Chautīśā Yantra is special because even more combinations of 4 numbers add up to 34. Try looking at:
Corners:
7 (top-left) + 14 (top-right) + 4 (bottom-right) + 9 (bottom-left)
7 + 14 + 4 + 9 = 34
2×2 squares:
13 + 8 + 3 + 10 (center 2×2) = 34
Same positions in different rows:
12 (1st row), 13 (2nd), 3 (3rd), 6 (4th)
12 + 13 + 3 + 6 = 34
This magic square has a lot of hidden combinations!
Magic Squares in History and Culture
Lo Shu Square – The Oldest Known Magic Square
The first recorded magic square is called the Lo Shu Square. It came from ancient China, more than 2000 years ago. Here's the story:
The Lo River flooded and the gods sent a turtle to help. The turtle had a special 3 × 3 grid on its back, made up of numbers 1 to 9. The pattern looked like this:

If you add:
Any row: 2 + 7 + 6 = 15
Any column: 2 + 9 + 4 = 15
Any diagonal: 2 + 5 + 8 = 15
So the magic sum = 15 in this case.
Where Else Are Magic Squares Found?
Magic squares have been studied in many countries like India, Japan, China, Central Asia, and Europe.
In India, ancient mathematicians created not only 3 × 3 but also 4 × 4, 5 × 5, and even bigger magic squares.
They found smart methods to build these squares without just guessing.
Ancient Magic Squares in Indian Temples
One such 3 × 3 magic square is found on a pillar in a temple in Palani, Tamil Nadu, dating back to the 8th century CE.

Magic squares are also found in homes and shops, especially in the Navagraha Yantra, which connects magic squares with planets like:

Each of these has a magic square inside it.
What is a Kubera Yantra?
The Kubera Yantra is a sacred diagram (or symbol) used in Indian tradition.
It is associated with Lord Kubera, the deity of wealth.
This Yantra often contains a magic square inside it.
The Magic Square in Kubera Yantra
Here’s the 3 × 3 grid from the image: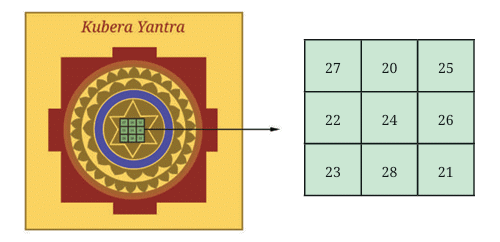
Let’s check if this is a magic square by calculating the sums of each row, column, and diagonal:
Rows:
Row 1: 27 + 20 + 25 = 72
Row 2: 22 + 24 + 26 = 72
Row 3: 23 + 28 + 21 = 72
Columns:
Column 1: 27 + 22 + 23 = 72
Column 2: 20 + 24 + 28 = 72
Column 3: 25 + 26 + 21 = 72
Diagonals:
27 + 24 + 21 = 72
25 + 24 + 23 = 72
✅ Yes! Every row, column, and diagonal adds up to 72. So, 72 is the magic sum here.
Why Is This Special?
Just like the Lo Shu Square with magic sum 15, the Kubera Yantra is a magic square—but with different numbers and a different magic sum.
It still follows the magic square rules: all rows, columns, and diagonals total the same.
But the numbers used are bigger: from 20 to 28.
This shows that magic squares can be built using different sets of numbers, not just 1 to 9.
Nature’s Favourite Sequence: The Virahāṅka- Fibonacci Numbers!
It's a special number pattern that looks like this:
1, 2, 3, 5, 8, 13, 21, 34, …
Each number (after the first two) is the sum of the previous two numbers:
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
and so on.
This sequence is also called the Fibonacci sequence, and it appears all around us—in plants, music, art, and nature!
Discovery of the Virahāṅka Numbers
Surprisingly, it first appeared in poetry, especially in Sanskrit, Tamil, Telugu, and other Indian languages.
In poetry:
A short syllable = 1 beat
A long syllable = 2 beats
Ancient poets used different combinations of these syllables to make up rhythms. So, they started asking:
“In how many ways can we fill a line of poetry with 8 beats using short (1) and long (2) syllables?”
Let’s Take an Example (n = 4 beats):
You want to write 4 beats using only 1s and 2s. Let’s list the combinations: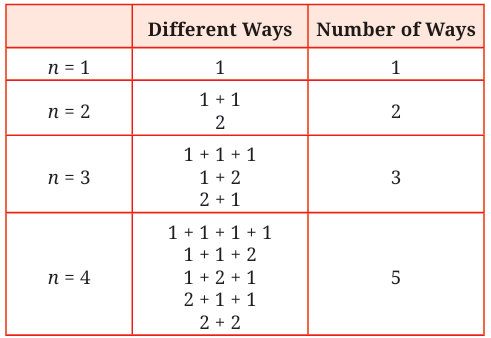
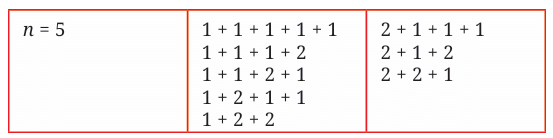
There are 5 ways to write 4 beats using 1s and 2s. This is the Fibonacci number at position 4 (starting from n=1).
How to Get the Next Fibonacci Number?
You use a systematic method:
Start with all the combinations for the previous number.
Add a 1 in front of all of them (for one short syllable)
Add a 2 in front of the combinations two steps before (for one long syllable)
This builds up the next number in the sequence!
Virahāṅka–Fibonacci Numbers
What is this sequence?
It’s a famous list of numbers:1, 2, 3, 5, 8, 13, 21, 34, 55...
Each number is found by adding the two numbers before it.
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
and so on...
This sequence is called the Fibonacci Sequence in the West, but Virahāṅka Numbers in India, after the Indian scholar Virahāṅka who discovered them around 700 CE, much before Fibonacci!
How did these numbers come up?
They came from poetry, not math!
In ancient Indian poetry:
A short syllable = 1 beat
A long syllable = 2 beats
Poets wanted to know:
How many ways can we make a poem line with 8 beats?
Each line can be filled with a mix of short (1 beat) and long (2 beat) syllables.
Let's take an example:
How many rhythms are possible for 5 beats?
Use only 1's and 2's. Let’s find all the ways to add up to 5:
1 + 1 + 1 + 1 + 1
1 + 1 + 1 + 2
1 + 1 + 2 + 1
1 + 2 + 1 + 1
2 + 1 + 1 + 1
1 + 2 + 2
2 + 1 + 2
2 + 2 + 1
That's 8 rhythms.
So, the number of ways to form rhythms for 5 beats is the 5th number in the Virahāṅka–Fibonacci sequence, which is 8!
Why does this work?
Because each rhythm either:
Starts with 1, then the rest must make (n - 1) beats
Starts with 2, then the rest must make (n - 2) beats
So: Ways to write n = Ways to write (n - 1) + Ways to write (n - 2)
That’s exactly how Fibonacci numbers grow!
History Fun Fact:
Virahāṅka introduced the numbers in India around 700 CE
Fibonacci used them in Europe only in 1202 CE
These numbers are in nature (pinecones, flowers), art, music, and poetry!

What’s the Rule for the Fibonacci Sequence?
To get the next number in the sequence, add the two numbers before it:
1, 2, 3, 5, 8, 13, 21, 34, 55
Next is: 34 + 55 = 89
Then: 55 + 89 = 144
Then: 89 + 144 = 233
Look at flowers like daisies. Many have 13, 21, or 34 petals.
Many have 13, 21, or 34 petals.
These are Fibonacci numbers!
Nature uses this pattern in:
Sunflower spirals
Pinecones
Pineapples
Flowers
This shows how deeply math and nature are connected.
Digits in Disguise
There is a math puzzle where numbers are replaced by letters. It’s called a cryptarithm or alphametic puzzle. The idea is to figure out which digit (from 0 to 9) each letter stands for so that the math equation makes sense.
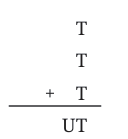
That means:
We are adding T + T + T, which is the same as 3 × T.
The answer is a 2-digit number: UT (U is the tens digit, T is the ones digit again!).
So we look for a number T such that 3 × T = UT, and the last digit of the answer is the same as T.
Try T = 5:
3 × 5 = 15 → Yes! The answer is 15 (U = 1, T = 5)
Next, we have: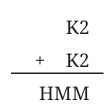
"K2" means a 2-digit number where the first digit is K and the second is 2.
Add it to itself: K2 + K2 = HMM
The answer is a 3-digit number HMM, where both M digits are the same.
Let’s try K = 6:
K2 = 62 → 62 + 62 = 124 → Not the right format.
Try K = 7:72 + 72 = 144 → H = 1, M = 4
⇒ HMM = 144
FAQs on Number Play Class 7 Notes Maths Chapter 6 Free PDF
| 1. What is the importance of understanding numbers in everyday life? |  |
| 2. How can I determine the parity of a number? |  |
| 3. What are some fun activities to explore numbers in grids? |  |
| 4. What are the basic divisibility rules I should know? |  |
| 5. What are cryptarithms and how can I solve them? |  |
















