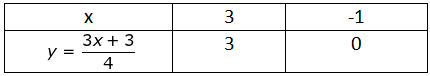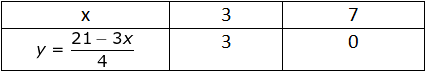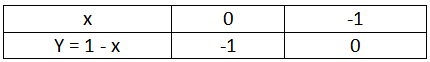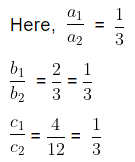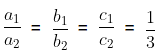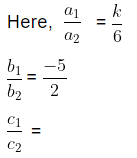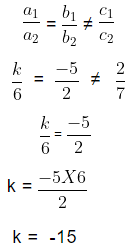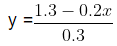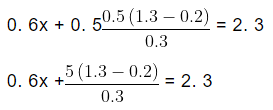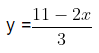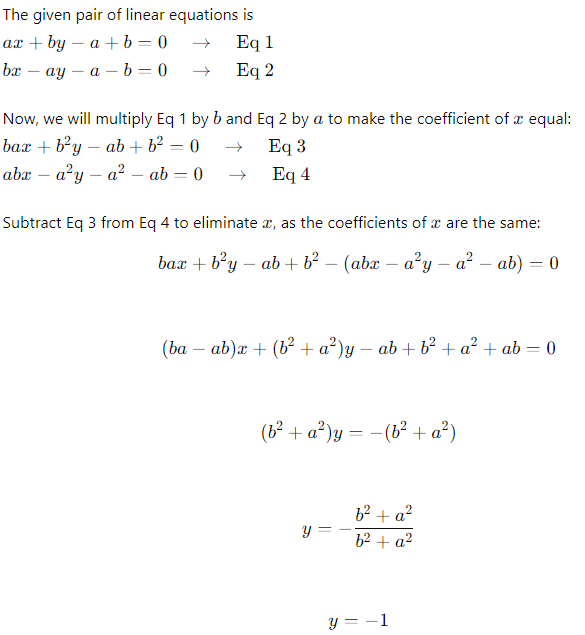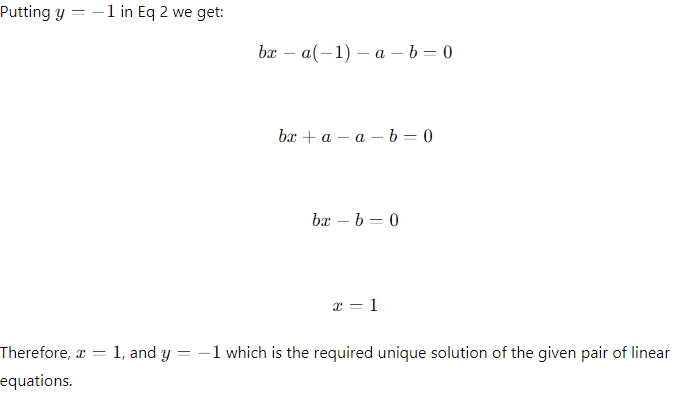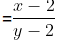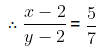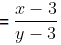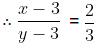Pair of Linear Equations in two Variables Class 10 Notes Maths Chapter 3
| Table of contents |

|
| Introduction |

|
| Pair of Linear Equations in Two Variables |

|
| Graphical Method of Solution of a Pair of Linear Equations |

|
| Algebraic Methods of Solving a Pair of Linear Equations |

|
| Summary |

|
Introduction
- Linear equations can be used to represent almost any situation involving an unknown quantity.
- We apply linear equations in various real-life situations like weather predictions, ingredients of a recipe, our monthly expenditure, predicting profit in business and Government surveys.
 Various forms of Linear Equation
Various forms of Linear Equation
- The general form of a linear equation in two variables is ax + by + c = 0, where a and b cannot be zero simultaneously.
Let us consider an example of a linear equation in two variables, x + 3y = 7.
LHS = x + 3y
If we substitute x=1 and y=2 into the LHS of the equation, we get:
LHS = x+3y = 1+3(2) = 7Here, LHS = RHS.
Thus, we can conclude that x=1 and y=2 is a solution to the equation x+3y=7.
Now, let's consider another pair of values for x and y.
Substituting x=2 and y=1 into the LHS of the equation, we get:
LHS = x+3y = 2+3(1) = 5Here, LHS RHS.
Therefore, x=2 and y=1 is not a solution to the equation x+3y = 7.
We know that the graph of a linear equation in two variables is a straight line.
If x=1 and y=2 is a solution of x+3y=7, then the point (1,2) lies on the line representing the equation x+3y = 7.
In the case of x=2 and y=1, which is not a solution, the point(2,1) does not lie on the line representing the equation x+3y = 7.
Thus, we conclude that every solution of the equation is a point on the line representing it.
Pair of Linear Equations in Two Variables
The general form for a pair of linear equations in two variables x and y is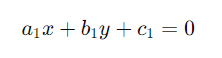
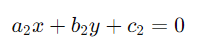
A pair of linear equations in two variables can have one of the following types of solutions:
1. Unique Solution
- When the two equations represent two distinct lines in a coordinate plane, and these lines intersect at a single point, there is a unique solution.
- Mathematically, this means that the lines are not parallel (their slopes are different), and they are not coincident (they do not represent the same line).
2. Infinitely Many Solutions
- If the two linear equations represent the same line in a coordinate plane, they have an infinite number of solutions.
- This occurs when the equations are essentially equivalent, and every point on the common line satisfies both equations.
3. No Solution
- When the two equations represent parallel lines that do not intersect, there is no solution.
- Mathematically, this means that the lines have the same slope (their coefficients are proportional), but they have different y-intercepts.
Example:
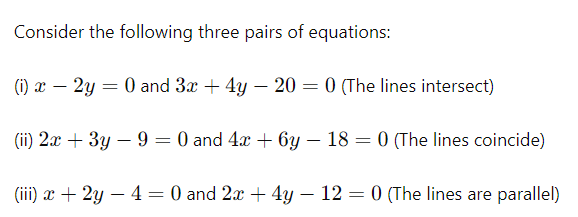
Graphical Representation of Linear Equation
We know that the geometrical representation of linear equations in two variables is a straight line, but when we have a pair of linear equations then there will be two straight lines, which are considered together.
When there are two lines in a plane, one of the following possibilities may arise.
(i) The two lines will intersect
(ii) The two lines are parallel
(iii) Two lines are coincident
Graphical Method of Solution of a Pair of Linear Equations
We know that a pair of linear equations is represented graphically by two straight lines and these lines may be parallel, may intersect or may coincide.
Now, we will consider certain cases here,
- If the two lines intersect each other at one point only, then we say that there is one and only one solution, that is, a unique solution exists for this pair of linear equations in two variables. Such a pair of linear equations is called a consistent pair of Linear equations.
- If the two lines are coincident then we say that the pair of linear equations has infinitely many solutions. Such a pair of linear equations is called an consistent pair of Linear equations.
- If the two lines are parallel to each other, that is, they do not meet at all, and then we say that the two linear equations have no common solution. Such a pair of linear equations is called a dependent pair of Linear equations.

If the lines represented by the equation,
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0 are,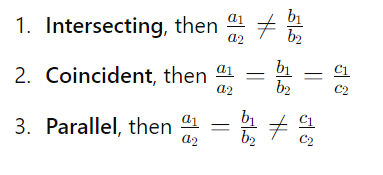
Let us consider some examples here, to understand better the above relations.
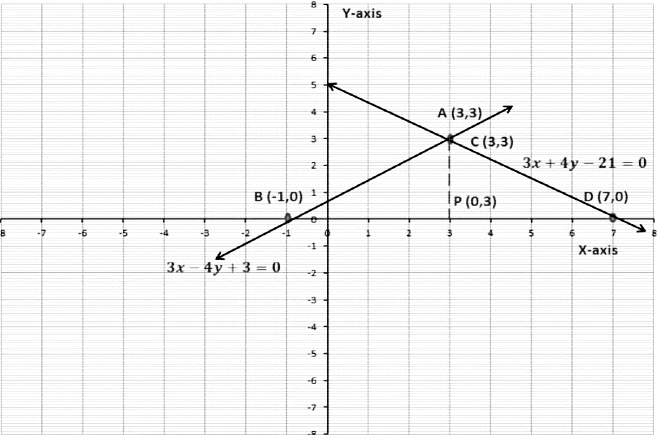
Example 1: Solve graphically the pair of linear equations 3x − 4y + 3 = 0 and 3x + 4y − 21 = 0. Find the coordinate of the vertices of the triangular region formed by these lines and X-axis. Also, calculate the area of this triangle.
Sol:
Firstly we will find two solutions for each equation.
(i) Table for 3x − 4y + 3 = 0
Let the points be A (3, 3) and B (-1,0)(ii) Table for 3x + 4y − 21 = 0
Let the points be C (3, 3) and D (7,0)
Now we will plot these points on a graph paper.
We will join points A and B, A and D respectively.
(Point A and Point C have the same coordinate)
When we join these points we will get a triangle ∆ ABD.
The coordinates of the vertices of ∆ ABD are,
A (3,3), B (-1,0) and D (7,0)
Next, we have to find the area ∆ ABD.
We know,
Area of a triangle = 1/2 × Base × Height
In ∆ ABD,
Base = 8 units
Height = 3 units
Area of ∆ ABD = 1/2 ×BD×AP
=12× 8 ×3 = 12 sq. units
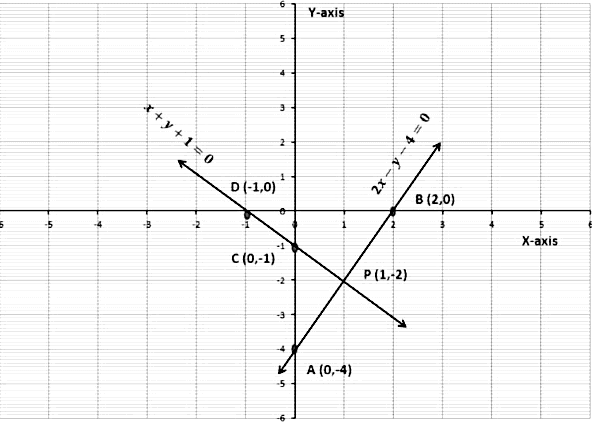
Example 2: Solve the following system of linear equations graphically:
2x − y − 4 = 0
x + y + 1 = 0
Sol:
The pair of linear equations is,
2x − y − 4 = 0
x + y + 1 = 0
First, we will find two solutions of each equation.
(i) Table for 2x − y − 4 = 0
Let the points be A(0,-4) and B(2,0)
(ii) Table for x + y + 1 = 0
Let the points be C (0,-1) and D (-1,0)
Now we plot these points on a graph paper.
We have joined points A and B, C and D respectively.
We see that the two lines are intersecting at point P (1, -2).
So the solution of the given pair of equations is x = 1 and y =−2.
Example 3: Form a pair of linear equations in two variables using the following information and solve it graphically. Five years ago, Mayank was twice as old as Rajat. Ten years later, Mayank’s age will be ten years more than Rajat’s age. Find their present ages.
Sol:
Let Mayank’s and Rajat’s present age be x years and y years respectively.
5 years ago,
Mayank’s age was (x − 5) years
Rajat’s age was (y − 5) years
Now it is given that 5 years ago Mayank was twice as old as Rajat.
∴ (x − 5) = 2(y − 5)
x − 5 = 2y − 10
x − 2y = −10 + 5
x − 2y = −5 → Eq.1
10 years later,
Mayank’s age will be (x + 10) years
Rajat’s age was (y + 10) years
It is given that 10 years later, Mayank’s age will be ten years more than Rajat’s age.∴ (x + 10) = (y + 10) + 10
x + 10 = y + 20
x − y = 10 → Eq.2
We get a pair of linear equations,
x − 2y + 5 = 0
x − y − 10 = 0
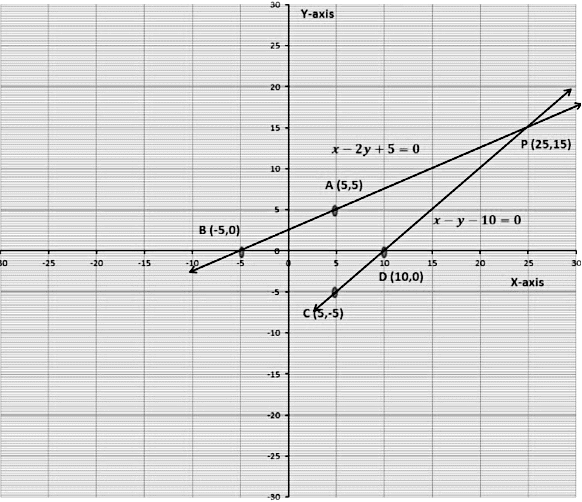
Now we draw the graph of Equations 1 and 2.
We will find two solutions of the two equations first
Table for x − 2y + 5 = 0Let the points be A (5, 5) and B(-5,0)
Table for x − y − 10 = 0
Let the points be C (5,-5) and D (10,0)
Now we plot these points on a graph paper.
Join points A and B to get, line AB
Join points C and D to get, line CD
We see that the lines AB and CD are intersecting at point P. The coordinate of points of P is (25, 15), that is, x = 25 years and y = 15 years
Mayank’s age = 25 years
Rajat’s age = 15 years
Example 4: Check whether the given pair of linear equations is consistent or inconsistent. x + 2y = 4 and 3x + 6y = 12
Sol:
The pair of linear equations is
x + 2y = 4
3x + 6y = 12
The standard form of pair of linear equations is
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
On comparing the linear equations with the standard form of equations we get,
a1 = 1, b1 = 2 and c1 = 4
a2 = 3, b2 = 6 and c2 = 12
We see that
Therefore, the given pair of linear equations is consistent.
Example 5: Find the value of ‘k’ for which the system of equations kx − 5y = 2 and 6x + 2y = 7 has no solution.
Sol:
The given pair of linear equations is,
kx − 5y = 2
6x + 2y = 7
We know the standard form of pair of linear equations is
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
On comparing the linear equations with the standard form of equations we get,a1 = k, b1 = −5 and c1 = 2
a2 = 6, b2 = 2 and c2 = 7
We know that a pair of linear equations has no common solution when,
Algebraic Methods of Solving a Pair of Linear Equations
The graphical method for solving a pair of linear equations is more suitable for integers but for non-integers, it may not be as accurate as we need. So, we use other algebraic methods to solve the pair of linear equations. 
Some of the algebraic methods which we are going to study now are
- Substitution Method
- Elimination Method
1. Substitution Method
In the substitution method, we find out the value of one variable in terms of the other variable and then we substitute this value in other equations to get an equation in one variable. Now, this equation can be solved easily.
Let us consider some examples to understand the substitution method better.
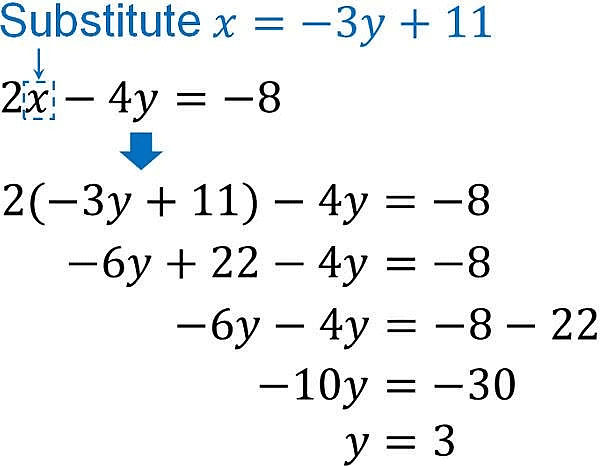 Example of Substitution Method
Example of Substitution Method
Example 6: Solve the following pair of linear equations by the substitution method.
0. 2x + 0. 3y = 1. 3 and 0. 6x + 0. 5y = 2. 3
Sol: The given pair of linear equations is
0. 2x + 0. 3y = 1. 3 →Eq 1
0. 6x + 0. 5y = 2. 3 →Eq 2
First, we find the value of variable y in terms of other variables, i.e. x.
From equation (1),
Next, we substitute the value of y in equation (2) From equation (2),
1. 8x + (6. 5 − x) = 2. 3 × 3
1. 8x + 6. 5 − x = 6. 9
0. 8x = 6. 9 − 6. 5
0. 8x = 0. 4
x = 0. 5
Putting the value of x in equation 1, we get
0. 2 × 0. 5 + 0. 3y = 1. 3
0. 3y = 1. 3 − 0. 01
0. 3y = 1. 29
y = 4. 3
Therefore, x = 0. 5 and y = 4. 3
Example 7: Solve 2x + 3y = 11 and 2x − 4y = −24 and hence find the value of m for which y = mx + 3.
Sol: The given pair of linear equations is
2x + 3y = 11 →Eq 1
2x − 4y = −24 →Eq 2
We will first find the value of variable y in terms of variable, x.
From equation (1),
Next substituting this value of y in equation (2), we get6x − (44 − 8x) = −24 × 3
6x + 8x − 44 = −72
14x = −72 + 44
14x = −28
x = −2
Putting the value of x in equation 1, we get
2 × (−2) − 4y = −24
−4 − 4y = −24
−4y = −24 + 4
−4y = −20
y = 5
Therefore, x = −2 and y = 5
Substituting the value of x and y in the equation
y = mx + 3, we get
5 = −2m + 3
m = −1
Example 8: The difference between the two numbers is 75 and on number is four times the other.
Sol:
Let the two numbers be x and y.
x > y
It is given that the difference between x and y is 75.
x − y = 75 → Eq 1
One number is four times the second number.
x = 4y →Eq 2
Substituting the value of x from Eq 2 in Eq 1, we get
4y − y = 75
3y = 75
y = 25
Substituting the value of y in Eq 2, we get
x = 4 × (25)
x = 100
The two numbers are 100 and 25.
2x + 3y = 9 x - y = 2
2. Elimination Method
Elimination Method is another method of eliminating one variable but in this method, one variable out of two variables is eliminated by making the coefficient of that variable equal in both the equations.
Now, we will consider some examples:
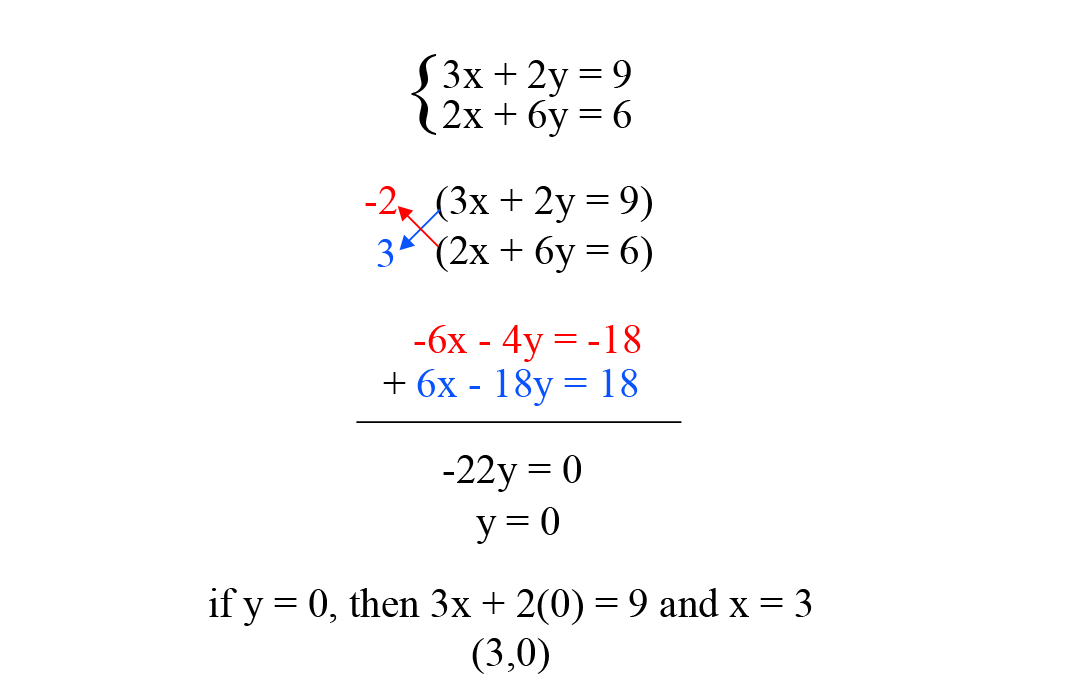 Example of Elimination Method
Example of Elimination Method
Example 9: Use the elimination method to find all possible solutions of the following pair of linear equations.
ax + by − a + b = 0 and bx − ay − a − b = 0
Sol:
Example 10: The sum of the digits of a two-digit number is 6. Also, seventeen times this number is five times the number obtained by reversing the order of the digits. Find the number.
Sol:
Let the digit at the unit place be x and the digit at tens place be y.
The Original two-digit number is 10y + x
The sum of the digits of the original number = 6
∴ y + x = 6
x + y − 6 = 0 → Eq 1
On reversing the order of the two-digit number, we get y at units place and x at the tens place.
∴ The new two-digit number= 10x + y
Seventeen times of the original number is equal to five the reversed number
17(10y + x) = 5(10x + y)
170y + 17x = 50x + 5y
170y − 5y = 50x − 17x
165y = 33x
x = 5y
x − 5y = 0 → Eq 2
On subtracting Eq 2 from Eq 1, we get
x + y − 6 − (x − 5y) = 0x + y − 6 − x + 5y = 0
6y = 6
y = 1
Substituting y = 1 in Eq 1
x + 1 − 6 = 0
x = 5
Therefore, the required two-digit number = 10y + x = 10 × 1 + 5 = 15
Example 11: A fraction becomes 5/7 , if 2 is subtracted to both the numerator and the denominator. If 3 is subtracted to both the numerator and denominator, it becomes 2/3. Find the fraction.
Sol:
Let the fraction be x/y
Subtracting 2 to both the numerator and denominator, we get new fraction
It is given that the new fraction obtained =5/7
7(x − 2) = 5(y − 2)7x − 14 = 5y − 10
7x − 5y = 14 − 10
7x − 5y = 4
7x − 5y − 4 = 0 → Eq 1
Next, we subtract 3 to both the numerator and denominator New fraction
It is given that the new fraction obtained = 2/3
3(x − 3) = 2(y − 3)
3x − 9 = 2y − 6
3x − 2y = 3
3x − 2y − 3 = 0 → Eq 2
7x − 5y − 4 = 0 → Eq 1
Multiplying Eq 1 by 3 and Eq 2 by 7 to make the coefficient of x equal, we get
21x − 15y − 12 = 0 → Eq 3
21x − 14y − 21 = 0 → Eq 4
Now, on subtracting, we get
21x − 15y − 12 − (21x − 14y − 21) = 0
21x − 15y − 12 − 21x + 14y + 21 = 0
−y + 9 = 0
y − 9 = 0
y = 9
Putting the value of y in Eq 1, we get
7x − 5(9) − 4 = 0
7x − 45 − 4 = 0
7x = 49
x = 7Therefore, the required fraction is 7/9 .
Example 12: The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10km, the charge paid is Rs. 110 and for a journey of 15 km the charge paid is Rs.160. What are the fixed charges and the charge per kilometer? How much does a person have to pay for traveling a distance of 25 km?
Sol:
Let fixed charge be Rs. x and charge per kilometer be Rs. y For 10 km distance, Fixed charge + charge per kilometer = Rs. 110
x + 10y = 110
x + 10y − 110 = 0 → Eq 1
For 15 km distance,
Fixed charge + charge per kilometer = Rs. 16
x + 15y = 160
x + 15y − 160 = 0 → Eq 2
Now subtracting Eq 2 from Eq 1 we get,
x + 15y − 160 − (x + 10y − 110) = 0
x + 15y − 160 − x − 10y + 110 = 0
15y − 10y − 50 = 0
5y − 50 = 0
y = 10
Substituting the value of y in Eq 1 we get,
x + 10y − 110 = 0
x + 10(10) − 110 = 0
x + 100 − 110 = 0
x = 10
Therefore, the fixed charge is Rs. 5 and the charge per kilometer is Rs. 10.
For 25 km distance,
Fixed charge + charge per kilometer = Rs. x + 25y
= Rs 10 + 25 (10)
= Rs 260
2x + 3y = 10 3x - 2y = 2
Summary
1. Solving Linear Equations:
- Linear equations in two variables can be solved through:
(i) Graphical method
(ii) Algebraic methods
2. Graphical Method:
- Graphs of linear equations form lines.
- If lines intersect, there is a unique solution (consistent).
- If lines coincide, there are infinitely many solutions (dependent and consistent).
- If lines are parallel, there is no solution (inconsistent).
3. Algebraic Methods:
- Solutions can be found through:
(i) Substitution method
(ii) Elimination method
4. Pair of Linear Equations:
- For equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0:
(i) If a1/a2 ≠ b1/b2, the equations are consistent.
(ii) If a1/a2 = b1/b2 ≠ c1/c2, the equations are inconsistent.
(iii) If a1/a2 = b1/b2 = c1/c2, the equations are dependent and consistent.
5. Mathematical Representation:
- Non-linear situations can be mathematically represented by transforming them into a pair of linear equations.
|
127 videos|584 docs|79 tests
|
FAQs on Pair of Linear Equations in two Variables Class 10 Notes Maths Chapter 3
| 1. How can we solve a pair of linear equations in two variables graphically? |  |
| 2. What are the algebraic methods of solving a pair of linear equations in two variables? |  |
| 3. Can a pair of linear equations in two variables have no solution? |  |
| 4. How do we determine if a pair of linear equations in two variables has infinitely many solutions? |  |
| 5. Why is it important to understand how to solve a pair of linear equations in two variables? |  |