Probability Class 10 Notes Maths Chapter 14
| Table of contents |

|
| What is Probability? |

|
| Empirical/ Experimental Probability |

|
| Theoretical Probability |

|
| Event and Outcome |

|
| Different Types of Events with Examples |

|
| Some Solved NCERT Examples |

|
What is Probability?
Probability is a way to understand how likely something is to happen using numbers. It's like measuring how uncertain an event's outcome is. We use a scale from 0 to 1, where 0 means it can't happen at all, and 1 means it's certain to happen. You can also think of this scale as percentages, where 0% means impossible and 100% means certain.
- For example , if we flip a coin, the chance of getting heads is the same as the chance of getting tails, both 1/2 or 50%. When we add these chances, we get a total probability of 1.

Empirical/ Experimental Probability
In Class IX, we explored experimental (or empirical) probabilities, based on actual experiment results. Empirical probability, also known as experimental probability, is the probability of an event based on actual experiments or observations. It is calculated by conducting an experiment multiple times and recording the outcomes.
Empirical Probability (P) = (Number of Times the Event Occurs) / (Total Number of Trials)
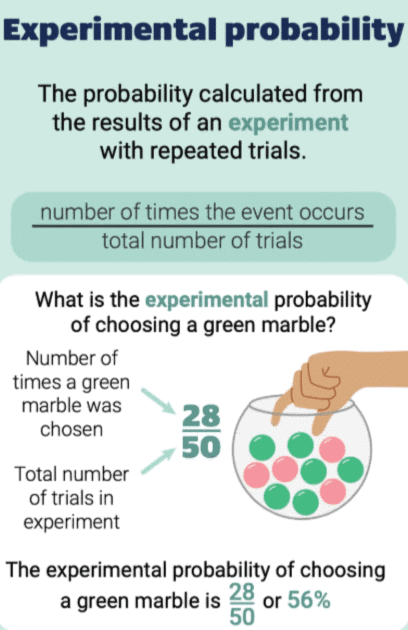
Example: Tossing a coin 1000 times resulted in 455 heads and 545 tails.
The empirical probability of heads is:
Empirical Probability of Heads: 455/1000 = 0.455
Empirical Probability of Tails: 545/1000 = 0.545
These probabilities are estimates, and outcomes may change with more trials.
Stabilization of Probabilities: As the number of trials increases, the empirical probability tends to stabilize around a certain value. The probability of getting a head in a coin toss tends to approach 0.5 as the number of tosses increases.
Theoretical Probability
The theoretical probability (also called classical probability) of an event E, written as P(E), is defined as
p(E) = (Number of outcomes favorable to E) / (Total number of possible outcomes)
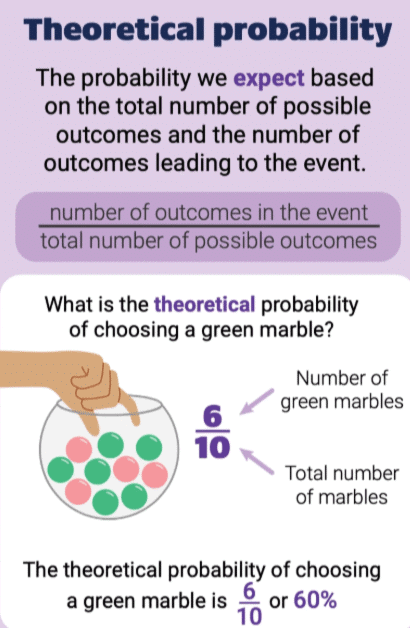
For example,
Question 1. What is the probability of getting head when we toss the coin?
Sol: The possible outcomes when tossing a coin are: Head or Tail.
- Number of possible outcomes = 2.
- Favourable outcome: Head.
- So, there is 1 favourable outcome.
Thus, the probability is:
p(E) = (Number of outcomes favorable to E) / (Total number of possible outcomes) = 1/2
Question 2. A bag contains a red ball, a blue ball, and a yellow ball, all the balls being of the same size. Kritika takes out a ball from the bag without looking into it. What is the probability that she takes out the (i) yellow ball? (ii) red ball? (iii) blue ball?
Sol:
(i) Probability of picking a yellow ball:
- Number of yellow balls = 1
- Total number of balls = 3
Probability of picking a yellow ball = 1/3
(ii) Probability of picking a red ball:
- Number of red balls = 1
- Total number of balls = 3
Probability of picking a red ball = 1/3
(iii) Probability of picking a blue ball:
- Number of blue balls = 1
- Total number of balls = 3
Probability of picking a blue ball = 1/3
Remarks:
- Each event in this example (yellow, red, blue) has only one possible outcome, making them elementary events.
- The sum of probabilities of all elementary events equals 1: P(Y) + P(R) + P(B) = 1
Question 3. Suppose we throw a die once.
(i) What is the probability of getting a number greater than 4?
(ii) What is the probability of getting a number less than or equal to 4?
Sol:
(i) Probability of getting a number greater than 4:
The numbers greater than 4 on a die are 5 and 6.
- Favorable outcomes = 2 (5, 6)
- Total possible outcomes = 6 (1, 2, 3, 4, 5, 6)
Probability = 2/6 = 1/3
(ii) Probability of getting a number less than or equal to 4:
The numbers less than or equal to 4 on a die are 1, 2, 3, and 4.
- Favorable outcomes = 4 (1, 2, 3, 4)
- Total possible outcomes = 6
Probability = 4/6 = 2/3
Event and Outcome
An outcome is the result of a random event, like rolling a die and getting a specific number (e.g., a 4). An event, on the other hand, is a collection of such outcomes. For example, rolling a die and hoping for a number less than 5 (which includes 1, 2, 3, and 4) is an event.
Example:
- Rolling a die and getting a 3 is an outcome.
- Rolling a die and getting a number less than 5 is an event.
(a) Tossing A Coin

If we toss a coin, it would be head or tail, only two outcomes.
(b) Tossing A Dice

A dice has six outcomes, numbering 1 to 6.
Question: A die is rolled once. What is the probability of getting a number greater than 4?
Sol: Total possible outcomes when rolling a die: 6 (1, 2, 3, 4, 5, 6)
Favorable outcomes for getting a number greater than 4: 5, 6
So, there are 2 favorable outcomes.
Probability P(E) is calculated as:
P(E) = Number of favorable outcomes / Total number of possible outcomes
= 2/6
= 1/3
(c) Experiment with a Deck of Cards
A deck of 52 playing cards contains 4 suits: Clubs, Diamonds, Hearts, and Spades.

- Hearts and Diamonds are red, while Clubs and Spades are black.
- There are 13 cards in each suit, comprising 26 red cards and 26 black cards.
- Each suit has 3 face cards: Jack, Queen, and King. So, there are 12 face cards in total (6 red and 6 black).
- The remaining cards are numbered Ace, 2 to 10.
(d) Example of Experiment: Tossing two dice
Now, there will be 6 outcomes of each dice, multiplied we will get 6×6 = 62 =36 Outcomes. They are:
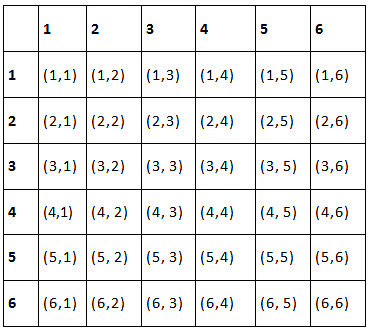
Question: Find the probability of getting a head when a coin is tossed once. Also
find the probability of getting a tail.
Sol: In the experiment of tossing a coin once, the number of possible outcomes
is two — Head (H) and Tail (T).
Let E be the event ‘getting a head’. The number of outcomes favourable to E, (i.e., of getting a head) is 1.
Therefore, P(E) = P (head) = Number of outcomes favourable to E/Number of all possible outcomes
P(E) =1/2
Similarly, if F is the event ‘getting a tail’, then
P(F) = P(tail) =1/2
Different Types of Events with Examples
1. Elementary Event
An elementary event refers to a single possible outcome.
Example:
- Flipping a coin and getting heads is an elementary event because it involves just one outcome.
- Similarly, rolling a die and getting a 6 is also an elementary event.
Question. If a coin is flipped once, what is the probability of getting tails?
Sol: Total possible outcomes when flipping a coin: 2 (Heads, Tails)
Favorable outcomes for getting tails: 1
So, there is 1 favorable outcome.
Probability P(T) is calculated as:
P(T) = Number of favorable outcomes / Total number of possible outcomes = 1/2
2. Sum of Probabilities
The sum of probabilities of all possible outcomes of an event must equal 1.
Example: When flipping a coin, the probability of heads is 1/2 and the probability of tails is 1/2.
Adding these together gives 1/2 + 1/2 = 1, which is the total probability.
Question. A bag contains 1 red ball, 2 blue balls, and 3 green balls. What is the probability of drawing a red ball or a blue ball from the bag?
Sol: Total number of balls: 1 (red) + 2 (blue) + 3 (green) = 6
Favorable outcomes for drawing a red ball or a blue ball: 1 (red) + 2 (blue) = 3
Probability of drawing a red ball or a blue ball P(E) is:
P(E) = Number of favorable outcomes / Total number of possible outcomes
= 3/6
= 1/2
3. Impossible and Sure Events
- An impossible event is one that can never happen, and its probability is 0.
- Example of Impossible Event:
Rolling a 7 on a standard die (since a die only has numbers 1-6) has a probability of 0. - A sure event is one that is certain to happen, with a probability of 1.
- Example of Sure Event:
Rolling a number less than 7 on a die has a probability of 1 because all possible outcomes (1-6) are less than 7.
Question: When rolling a standard six-sided die, what is the probability of rolling a number greater than 6? What is the probability of rolling a number less than or equal to 6?
Sol:
Total possible outcomes when rolling a die: 6 (1, 2, 3, 4, 5, 6)Favorable outcomes for rolling a number greater than 6: None (as the die only has numbers 1 through 6).
(i) Probability of rolling a number greater than 6:
P(Greater than 6) = 0/6 = 0
(ii) Probability of rolling a number less than or equal to 6:
Favorable outcomes for rolling a number less than or equal to 6: 1, 2, 3, 4, 5, 6 (all outcomes).
P(Less than or equal to 6) = 6/6 = 1
4. Range of Probability
- Probabilities always fall between 0 and 1.
- A probability of 0 means the event is impossible, and a probability of 1 means the event is certain.
- Hence, the probability of happening any event lies between 0 and 1
Let E be the event , then
0 ≤ P(E) ≤ 1
5. Complementary Events
Complementary events are outcomes that together cover all possibilities. If one event happens, the other cannot.
If E is an event, the event not E (denoted as E') represents the complement of E.
The sum of the probabilities of an event and its complement is always 1:
P(E)+P(not E)=1
Example:
When flipping a coin, the two outcomes—heads and tails—are complementary events. The probability of heads plus the probability of tails equals 1.
Question. A deck of cards has 52 cards, including 4 suits: Hearts, Diamonds, Clubs, and Spades. Each suit has 13 cards. What is the probability of drawing a card that is not a heart?
Sol:
- Total number of cards: 52
- Number of hearts: 13
- Number of non-heart cards:
Probability of drawing a non-heart card P(E′):
P(E′) = Number of non-heart cards / Total number of cards = 39/52 = 3/4
To confirm, the probability of drawing a heart is:
P(Heart) = 13/52 = 1/4
Since the sum of the probabilities of drawing a heart and not drawing a heart should be 1:
P(Heart) + P(Not Heart) = 1/4 + 3/4 = 4/4 = 1
Some Solved NCERT Examples
Question 1. If P(E) = 0.05, what is the probability of ‘not E’?Sol:
We know that,
P(E)+P(not E) = 1
It is given that, P(E) = 0.05
So, P(not E) = 1 - P(E)
Or, P(not E) = 1 - 0.05
∴ P(not E) = 0.95
Question 2. It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Sol:
Let the event wherein 2 students having the same birthday be E
Given, P(E) = 0.992
We know,
P(E)+P(not E) = 1
Or, P(not E) = 1–0.992 = 0.008
∴ The probability that the 2 students have the same birthday is 0.008
Question 3. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is
(i) red?
(ii) not red?
Sol: The total number of balls = No. of red balls + No. of black balls
So, the total number of balls = 5+3 = 8
We know that the probability of an event is the ratio between the number of favourable outcomes and the total number of outcomes.
P(E) = (Number of favourable outcomes/Total number of outcomes)
(i) Probability of drawing red balls = P (red balls) = (no. of red balls/total no. of balls) = 3/8
(ii) Probability of drawing not red balls = Probability of drawing black balls = P (black balls) = (no. of black balls/total no. of balls) = 5/8
Question 4. A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be
(i) red?
(ii) white?
(iii) not green?
Sol:
The Total no. of balls = 5+8+4 = 17
P(E) = (Number of favourable outcomes/ Total number of outcomes)
(i) Total number of red balls = 5
P (red ball) = 5/17≈ 0.29
(ii) Total number of white balls = 8
P (white ball) = 8/17 ≈ 0.47
(iii) Total number of green balls = 4
P (green ball) = 4/17 ≈ 0.23
∴ P (not green) = 1 - P(green ball) = 1 - (4/17) ≈ 0.76
|
127 videos|584 docs|79 tests
|
FAQs on Probability Class 10 Notes Maths Chapter 14
| 1. What is the difference between empirical probability and theoretical probability? |  |
| 2. Can you explain what an event and an outcome are in probability? |  |
| 3. What are some different types of events in probability, and can you provide examples? |  |
| 4. How can I calculate experimental probability with an example? |  |
| 5. What are some solved examples in NCERT related to probability? |  |
















