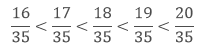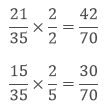Rational Numbers Class 7 Notes Maths Chapter 1
Introduction
In your study of numbers, you started by counting objects around you.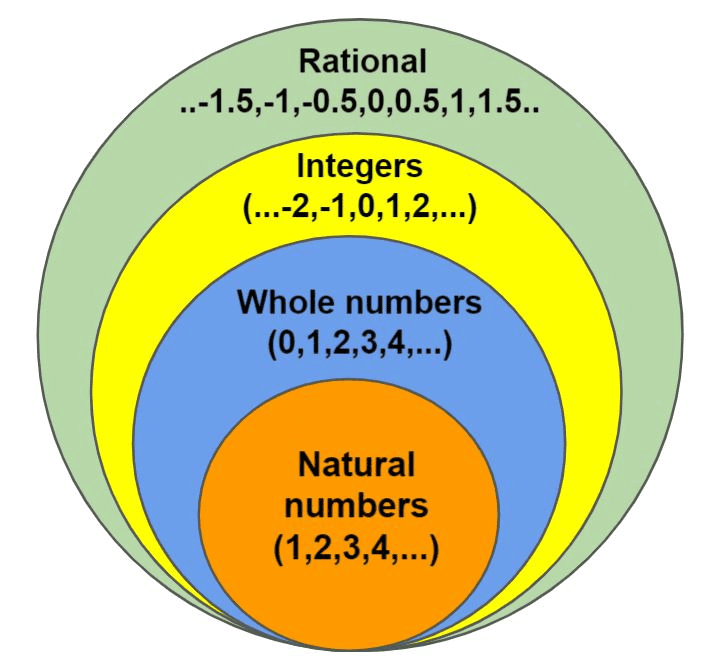
- Natural Numbers: The numbers you use for counting are called counting numbers or natural numbers. They are 1, 2, 3, 4, and so on.
- Whole Numbers: When we include 0 with natural numbers, we get the whole numbers, which are 0, 1, 2, 3, and so on.
- Integers: Then we combined the negatives of natural numbers with whole numbers to create integers. Integers are numbers like -3, -2, -1, 0, 1, 2, 3, and so on.
- Fractions, which are numbers written in the form of numerator/denominator, where the numerator can be 0 or a positive whole number, and the denominator is a positive whole number.
- Need for Rational Numbers: While integers represent whole values and their opposites, some situations require fractional values (e.g., -3/4 km to denote distance below sea level), necessitating an expanded number system to include rational numbers.
- Focus of this chapter: In this chapter, we will introduce the concept of rational numbers, along with exploring how to add, subtract, multiply, and divide them.
What are Rational Numbers?
A rational number is a number that can be written in the form p/q, where p and q are integers and q ≠ 0.
- The denominator q cannot be zero.
- All numbers, including whole numbers, integers, fractions and decimal numbers, can be written in the numerator/denominator form.
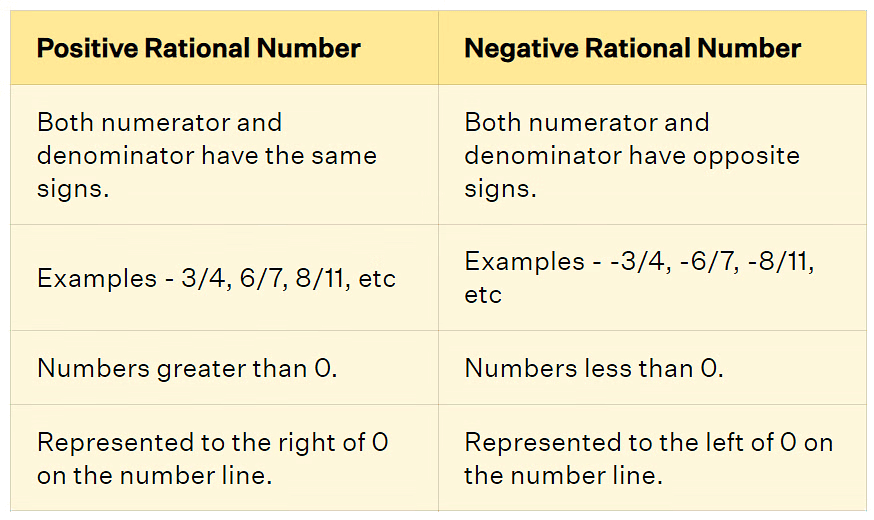
- Positive Rational Number: A rational number is positive if both p and q are either both positive or both negative. Positive rational numbers are represented to the right of 0 on the number line.
- Negative Rational Number: It is negative if one of p or q is negative. Negative rational numbers are represented to the Left of 0 on the number line.
- Equivalent Rational Number: By multiplying or dividing both the numerator and the denominator of a rational number by the same non-zero integer, we can get another rational number that is equivalent to the given rational number.
- The standard form of Rational Number: A rational number is in its standard form if the numerator and denominator are co-prime (i.e., their greatest common divisor is 1) and the denominator is positive. To convert a rational number to its standard form, divide the numerator and denominator by their Highest Common Factor (HCF). If the denominator is negative, factor out the negative sign to ensure a positive denominator.
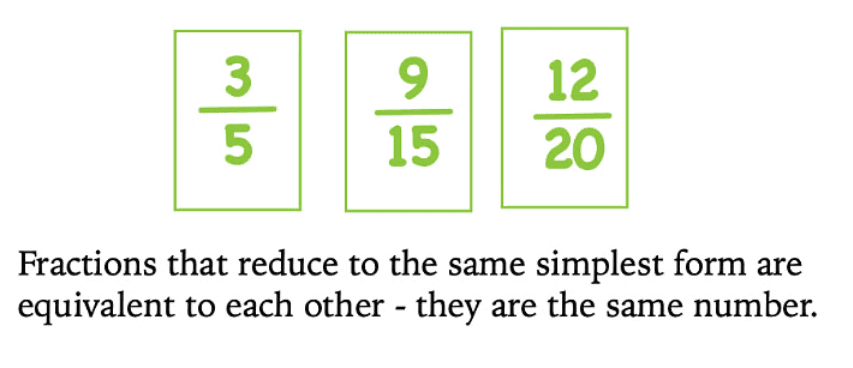
Properties of Rational Numbers
(a) Closure Property
Definition: If you can perform a mathematical operation (like addition or multiplication) on two numbers and always get a result that is still within the same set of numbers, then that set is said to be "closed" under that operation.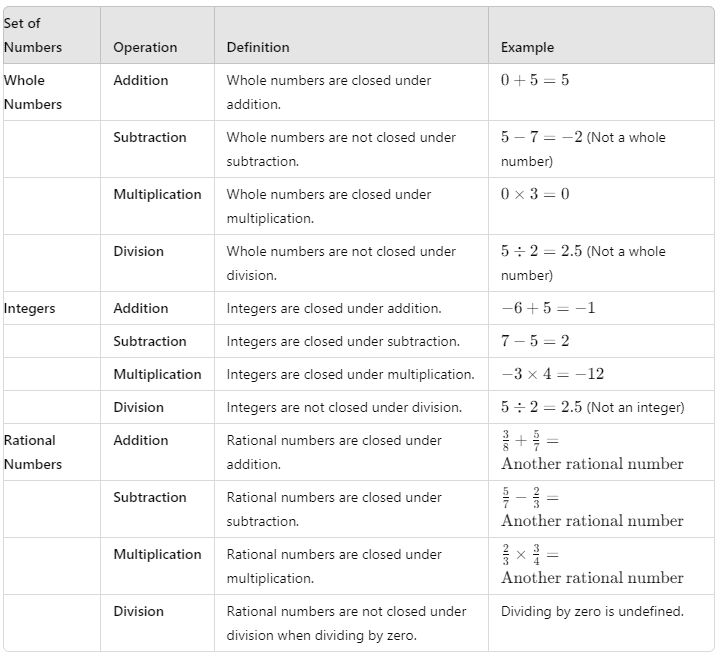 Closure property application to sets of numbers and operations.
Closure property application to sets of numbers and operations.
(b) Commutativity Property
Definition: An operation is commutative if you can change the order of the numbers and still get the same result.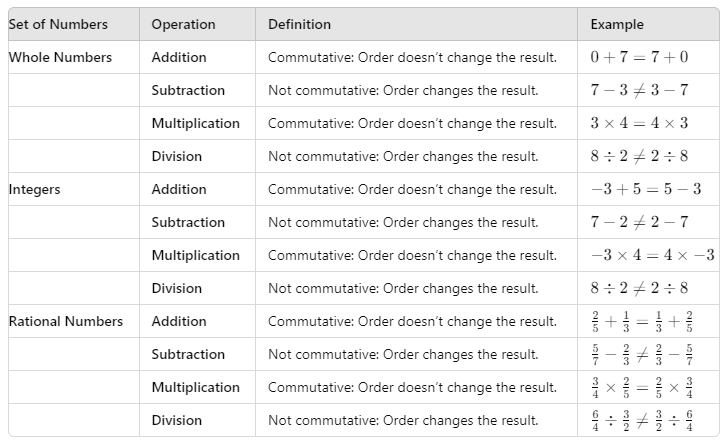 Commutativity property for different sets of numbers and operations
Commutativity property for different sets of numbers and operations
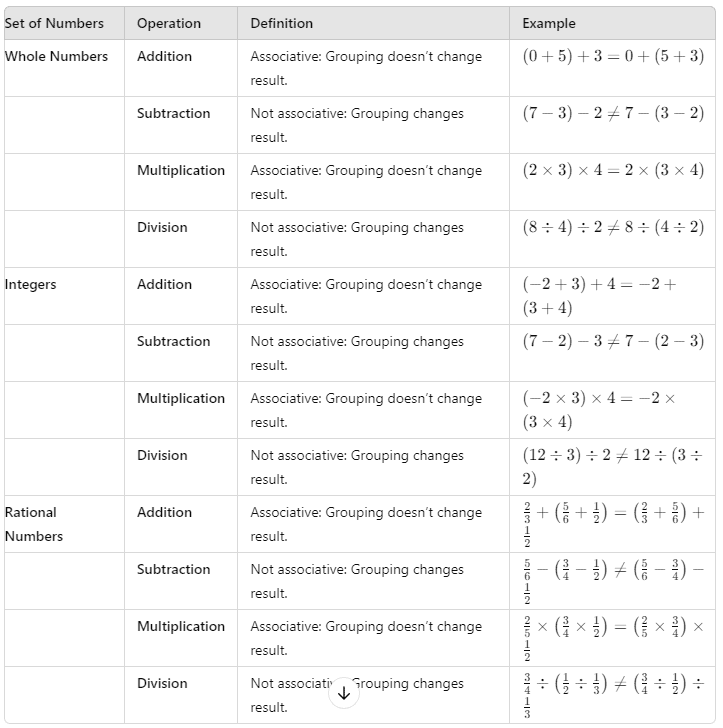
(b) Associativity Property
Definition: An operation is associative if the way you group the numbers does not change the result.
The Role of Zero (0):
Zero plays a fundamental role in mathematics as the identity element for addition. It does not change the value of other numbers when added to them.
- Addition with Whole Numbers:
- 2+0=0+2=2
- Adding zero to a whole number results in the same whole number.
- In general, a+0=0+a=a, where a is a whole number.
- Addition with Integers:
- −5+0=0+(−5)=−5
- Adding zero to an integer yields the same integer.
- In general, b + 0=0 + b = b, where b is an integer.
- Addition with Rational Numbers:
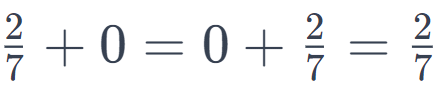
- Adding zero to a rational number results in the same rational number.
- In general, c+0=0+c=c, where c is a rational number.
- Identity for Addition:
- Zero is called the identity for the addition of rational numbers.
- It serves as the additive identity for integers and whole numbers as well.
The Role of 1:
- Multiplication with Whole Numbers:
- 5 × 1 = 1 × 5 = 5
- Multiplying any whole number by 1 gives the same whole number.
- In general, a × 1 = 1× a = a for any whole number a.
- Multiplication with Rational Numbers:
- Multiplying any rational number by 1 results in the same rational number.
- In general, a × 1 = 1 × a = a for any rational number a.
- Multiplicative Identity:
- 1 is called the multiplicative identity for rational numbers.
- It is also the multiplicative identity for integers and whole numbers.
Negative of a Number:
=> For integers, the negative of a number is found by adding the additive inverse.
- 1+(−1)=(−1)+1=0, so the negative of 1 is -1.
- 2+(−2)=(−2)+2=0, making 2 the negative or additive inverse of -2, and vice versa.
- In general, for an integer a, a+(−a)=(−a)+a=0.
=>For rational numbers, similar principles apply.
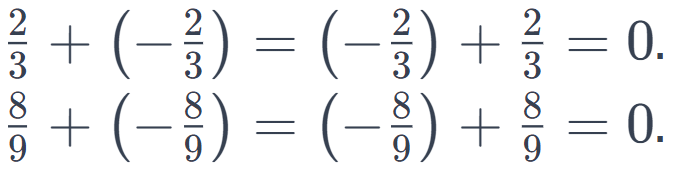
In general, for a rational number 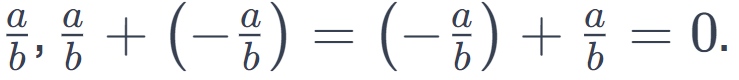
Reciprocal of a Number:
The reciprocal or multiplicative inverse of a rational number 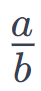 is another rational number
is another rational number 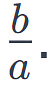
For example, 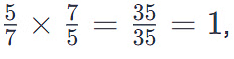
Zero has no reciprocal because there is no rational number that, when multiplied by 0, results in 1.
Zero has no reciprocal because there is no rational number that, when multiplied by 0, results in 1.
In general, if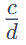 is the reciprocal of
is the reciprocal of 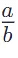 , then
, then 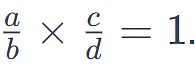
Operations on Rational Numbers
Addition of Rational Numbers
Same Denominator: If two rational numbers have the same denominator, simply add their numerators. The denominator remains unchanged.
Example: =1Different Denominators: Convert the rational numbers to have a common denominator before adding. Find equivalent fractions with the same denominator, then add the numerators. Example:
Additive Inverses: Two rational numbers whose sum is zero are additive inverses of each other. Example: &
Subtraction of Rational Numbers
Same Denominator: If the rational numbers have the same denominator, subtract their numerators. The denominator remains the same. Example:
Different Denominators: Convert to equivalent rational numbers with a common denominator before subtracting. Subtract the numerators and keep the common denominator. Example:
Multiplication of Rational Numbers
Multiply the numerators together and the denominators together. Maintain the signs correctly. Example:
Reciprocals: Two rational numbers whose product is 1 are reciprocals of each other. Example: and ;
A rational number and its reciprocal will always have the same sign.
Division of Rational Numbers
- To divide by a rational number, multiply by its reciprocal. Example:
Some Solved Examples on Above Concepts
Example 1: Simplify the rational number -16/(-24)
Ans:
Step 1: Identify the common factors of both numerator and denominator. In this case, the common factors are 2, 4, and 8.
Step 2: Divide both numerator and denominator by the greatest common factor, which is 8.
(-16) ÷ 8 = - 2
(-24) ÷ 8 = - 3
So, -16/(-24) simplifies to -2/-3 =x 2/3
Example 2: Add the rational numbers 2/5 and 3/10
Ans:
Step 1: Find the least common denominator (LCD) of both denominators. In this case, the LCD is 10.
Step 2: Convert both fractions to equivalent fractions with the LCD as the new denominator.
2/5 = 4/10 (multiply both numerator and denominator by 2)
3/10 = 3/10 (no change needed)
Step 3: Add the equivalent fractions.
4/10 + 3/10 = (4 + 3) / 10 = 7/10
So, 2/5 + 3/10 = 7/10.
Example 3: Using appropriate properties, find:
-2/3 × 3/5 + 5/2 – 3/5 × 1/6
Solution:
-2/3 × 3/5 + 5/2 – 3/5 × 1/6
= -2/3 × 3/5– 3/5 × 1/6+ 5/2 (by commutativity)
= 3/5 (-2/3 – 1/6)+ 5/2
= 3/5 ((- 4 – 1)/6)+ 5/2
= 3/5 ((–5)/6)+ 5/2 (by distributivity)
= – 15 /30 + 5/2
= – 1 /2 + 5/2
= 4/2
= 2
Example 4: Using appropriate properties, find:
2/5 × (- 3/7) – 1/6 × 3/2 + 1/14 × 2/5
2/5 × (- 3/7) – 1/6 × 3/2 + 1/14 × 2/5
= 2/5 × (- 3/7) + 1/14 × 2/5 – (1/6 × 3/2) (by commutativity)= 2/5 × (- 3/7 + 1/14) – 3/12
= 2/5 × ((- 6 + 1)/14) – 3/12
= 2/5 × ((- 5)/14)) – 1/4
= (-10/70) – 1/4
= – 1/7 – 1/4
= (– 4– 7)/28
= – 11/28
Example 5: Verify that: -(-x) = x for:
(i) x = 11/15
(ii) x = -13/17
Solution:
(i) x = 11/15
We have, x = 11/15
The additive inverse of x is – x (as x + (-x) = 0).
Then, the additive inverse of 11/15 is – 11/15 (as 11/15 + (-11/15) = 0).
The same equality, 11/15 + (-11/15) = 0, shows that the additive inverse of -11/15 is 11/15.
Or, – (-11/15) = 11/15
i.e., -(-x) = x
(ii) -13/17
We have, x = -13/17
The additive inverse of x is – x (as x + (-x) = 0).
Then, the additive inverse of -13/17 is 13/17 (as 13/17 + (-13/17) = 0).
The same equality (-13/17 + 13/17) = 0, shows that the additive inverse of 13/17 is -13/17.
Or, – (13/17) = -13/17,
i.e., -(-x) = x
Comparing Two Rational Numbers
While comparing positive rational numbers with the same denominator, the number with the greatest numerator is the largest. It is easy to compare these numbers if their denominators are the same.Eg:
A positive rational number is always greater than a negative rational number. While comparing negative rational numbers with the same denominator, compare their numerators ignoring the minus sign. The number with the greatest numerator is the smallest.
Positive rational numbers lie to the right of 0, while negative rational numbers lie to the left of 0 on the number line.
To compare rational numbers with different denominators, convert them into equivalent rational numbers with the same denominator, which is equal to the LCM of their denominators. You can find infinite rational numbers between any two given rational numbers.
Representation of Rational Numbers on the Number Line
Representation of whole numbers, natural numbers and integers on a number line is done as follows
 Rational Numbers can also be represented on a number line like integers i.e. positive rational numbers are on the right to 0 and negative rational numbers are on the left of 0.
Rational Numbers can also be represented on a number line like integers i.e. positive rational numbers are on the right to 0 and negative rational numbers are on the left of 0.
Representation of rational numbers can be done on a number line as follows:
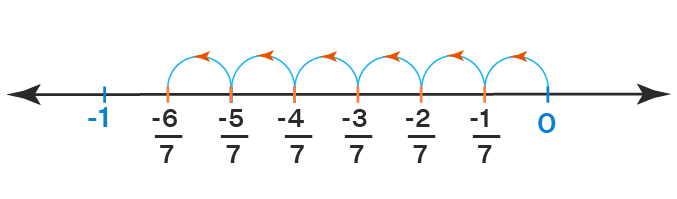
Between any two rational numbers, there are infinitely many rational numbers.
Rational Numbers between Two Rational Numbers
To find the rational numbers between two rational numbers, we have to make their denominator the same then we can find the rational numbers.
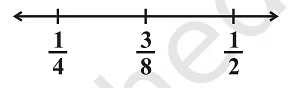
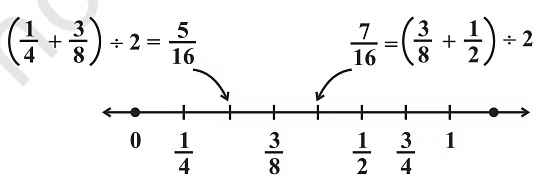
Example: Find three rational numbers between 1/4 and 1/2.
Ans:
(i) First, we find the mean of given numbers.
Mean is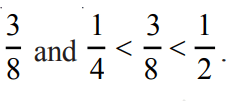
(ii) Again we find another rational number between 1/4 and 3/8 .For this, again we calculate mean of 1/4 and 3/8.
Mean is 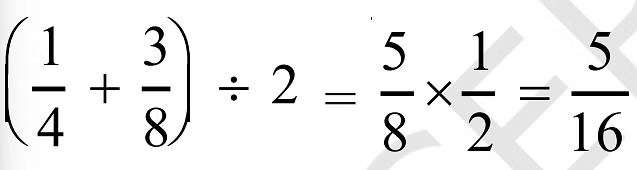
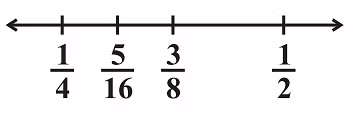
(iii) For the third rational number, we again find mean of 3/8 and 1/2.
Mean is 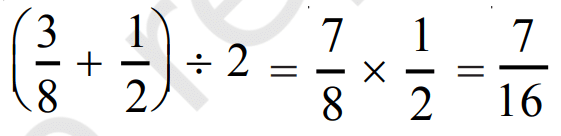
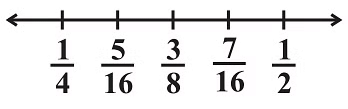
Hence, 5/16, 3/8, and 7/16 are 3 rational numbers between 1/4 and 1/2.
Example: Find rational numbers between 3/5 and 3/7.
Ans: To find the rational numbers between 3/5 and 3/7, we have to make their denominator same.
LCM of 5 and 7 is 35.Hence the rational numbers between 3/5 and 3/7 are
These are not the only rational numbers between 3/5 and 3/7.
If we find the equivalent rational numbers of both 3/5 and 3/7 then we can find more rational numbers between them.Hence we can find more rational numbers between 3/5 and 3/7.
Remark: Between any two given rational numbers, we need not necessarily get an integer but there are countless rational numbers between them.
Hope you’ve grasped the chapter thoroughly. For a more enriching learning experience, check out this video.
|
77 videos|386 docs|39 tests
|
FAQs on Rational Numbers Class 7 Notes Maths Chapter 1
| 1. What is the need for understanding Rational Numbers in mathematics? |  |
| 2. How are Rational Numbers defined and what sets them apart from other types of numbers? |  |
| 3. What are some properties of Rational Numbers that make them unique? |  |
| 4. How do you perform operations on Rational Numbers, such as addition, subtraction, multiplication, and division? |  |
| 5. Can Rational Numbers be both positive and negative, and how do we differentiate between the two? |  |