Subtraction Chapter Notes | Mathematics Class 3 ICSE PDF Download
Introduction
Subtraction is taking away some things from a group to find out how many are left. It’s the opposite of addition. We use the minus sign (-). The number you start with is the minuend, the number you take away is the subtrahend, and the answer is the difference.
Example: 8 - 3 = 5 (8 pencils, take away 3, 5 left).

Subtraction of Numbers (Without Borrowing)
We always start subtracting from the ones place and move towards the left.
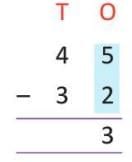
Example 1: 45 - 32 = ?
- Ones: 5 - 2 = 3.
- Tens: 4 - 3 = 1.
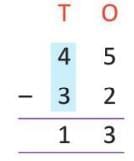
- Answer: 13.
Example 2: Subtract 489 - 256.
Sol: Write the numbers in a vertical format, aligning the digits by place value:
Ones place: 9 - 6 = 3
Tens place: 8 - 5 = 3
Hundreds place: 4 - 2 = 2
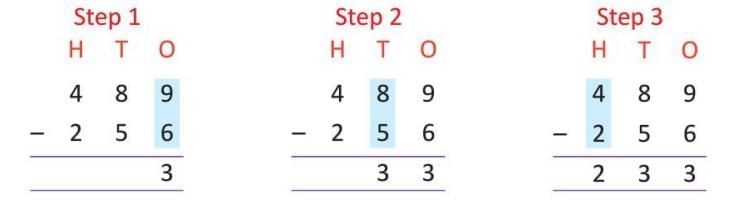 So, the result is: 233
So, the result is: 233
Answer: 489 - 256 = 233.
Subtraction of Numbers (With Borrowing)
If the ones digit you’re subtracting is bigger, borrow 1 ten from the tens place. This makes the ones place bigger so you can subtract.
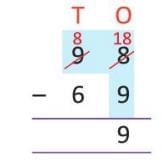
Example: 98 - 69 = ?
- Ones: 8 < 9, so borrow 1 ten. 9 tens become 8 tens, 8 ones become 18 ones.
- Subtract: 18 - 9 = 9 ones.
- 8 - 6 = 2 ten.
- Answer: 29.
Subtraction Facts
- If 0 is subtracted from a number, the result is the number itself.
- For example, 116 - 0 = 116.
- If 1 is subtracted from a number, the result is the predecessor of that number.
- For example, 243 - 1 = 242.
- If the same number is subtracted from itself, the result is 0.
- For example, 511 - 511 = 0.
- The order of numbers in subtraction cannot be changed because a bigger number cannot be subtracted from a smaller number.
- For example, 823 - 463 = 360, but 463 - 823 is not possible since 463 < 823.
Subtraction Using Expanded Form
Expanded form means breaking a number into its place values (tens and ones). For subtraction, we write both numbers in expanded form, subtract the ones and tens separately, and then combine the results.
Steps:
- Write both numbers in expanded form (e.g., 45 = 40 + 5).
- Subtract the ones, then the tens.
- Add the results to get the final answer.
Example: 56 – 23 = ?
- 56 = 50 + 6
- 23 = 20 + 3
- Subtract ones: 6 – 3 = 3
- Subtract tens: 50 – 20 = 30
- Combine: 30 + 3 = 33
- Answer: 33
Estimating the Difference
Estimating means guessing the answer to a subtraction problem by rounding numbers to make them easier to subtract. We usually round to the nearest 10. This gives us a close answer, not the exact one.
Steps:
- Round the minuend and subtrahend to the nearest 10, 100, 1000.
- Subtract the rounded numbers.
Example: Estimate 67 – 32.
- 67 rounds to 70 (because 67 is closer to 70 than 60).
- 32 rounds to 30 (because 32 is closer to 30 than 40).
- Subtract: 70 – 30 = 40
- Estimated difference: 40 (actual answer is 35, so it’s close!).
Example: Estimate 89 – 44.
- 89 rounds to 90.
- 44 rounds to 40.
- 90 – 40 = 50
- Estimated difference: 50 (actual answer is 45).
Word Problems
Word problems are stories that use subtraction to solve real-life situations. Read the problem carefully, find the numbers, and decide what to subtract.
Example: Ria had 50 balloons, and 20 burst. How many balloons are left?
- Numbers: 50 (total balloons), 20 (burst balloons).
- Subtract: 50 – 20 = 30
- Answer: 30 balloons are left.
Mixed Problems of Addition and Subtraction
To solve a problem that contains addition as well as subtraction, we follow the given steps:
- First, add the numbers that do not have a minus (-) sign in front of them and then add the numbers that have a minus sign separately.
- Subtract the smaller sum from the bigger sum.
Example: Solve 415 + 132 - 87 - 56.
Sol: Step 1: Add the numbers that do not have a minus (-) sign in front of them.
These numbers are 415 and 132.
415 + 132 = 547
Step 2: Add the numbers that have a minus (-) sign in front of them.
These numbers are 87 and 56 (from -87 and -56).
87 + 56 = 143
Step 3: Subtract the smaller sum (from Step 2) from the bigger sum (from Step 1).
The sum from Step 1 is 547, and the sum from Step 2 is 143.
547 - 143 = 404
Subtraction of 2-Digit Numbers Mentally
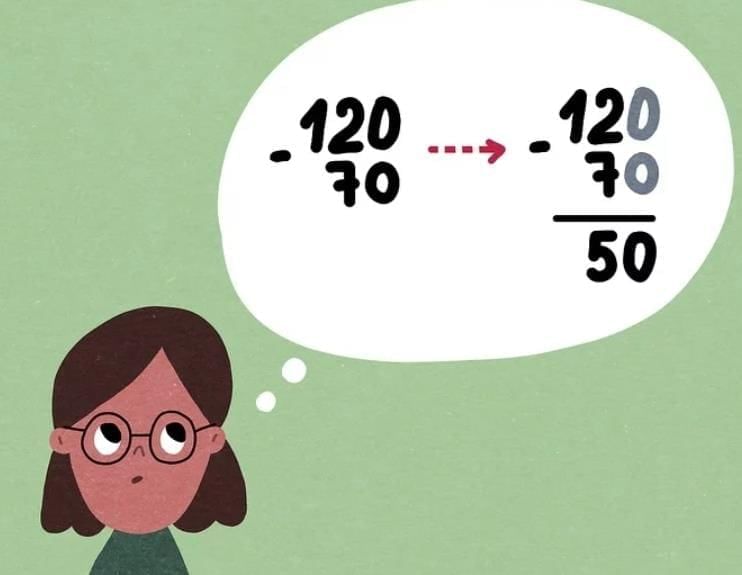
Mental subtraction means solving subtraction problems in your head without writing them down. Use tricks like breaking numbers into tens and ones or using subtraction facts.
Example: 48 – 23 = ?
- Think: 48 is 40 + 8, and 23 is 20 + 3.
- Subtract tens: 40 – 20 = 20
- Subtract ones: 8 – 3 = 5
- Combine: 20 + 5 = 25
- Answer: 25
Practice Questions
- Subtract 45 – 22 (without borrowing).
- Subtract 53 – 29 (with borrowing).
- Use expanded form to solve 67 – 34.
- Estimate the difference: 78 – 41.
- Solve the word problem: A basket has 60 oranges, and 25 are eaten. How many oranges are left?
|
67 docs|9 tests
|
FAQs on Subtraction Chapter Notes - Mathematics Class 3 ICSE
| 1. What is the difference between subtraction without borrowing and subtraction with borrowing? |  |
| 2. How can I practice subtraction facts effectively? |  |
| 3. What is expanded form in subtraction, and how is it used? |  |
| 4. How do you estimate the difference when subtracting two numbers? |  |
| 5. What types of word problems can involve subtraction for 3rd graders? |  |