Circles Class 10 Worksheet Maths Chapter 10
Multiple Choice Question
Q1: If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is: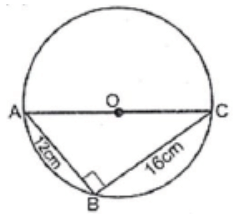 (a) 6 cm
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm
Ans: (c)
AB is perpendicular to BC, therefore ABC is a right triangle.
In right ΔABC , we have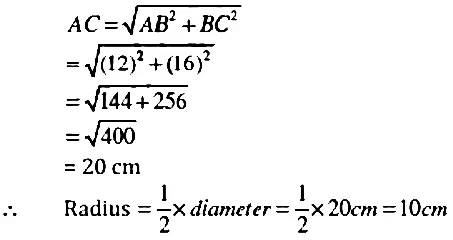
Q2: In Fig, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to: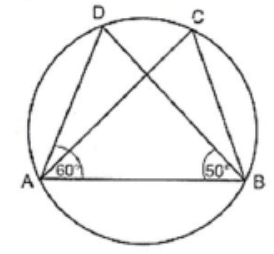 (a) 60º
(a) 60º
(b) 50º
(c) 70º
(d) 80º
Ans: (c)
In ΔADB, we have
∠A+∠B +∠D =180
⇒ 60º + 50º +∠D =180º
⇒ ∠D =180 −110 = 70º
i.e., 0 ∠ABD = 70º
Now, ∠ACB = ∠ADB = 70º
[∵Angles in the same segment of a circle are equal]
Hence, (c) is the correct answer.
Q3: AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is: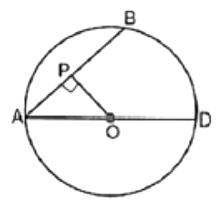 (a) 17 cm
(a) 17 cm
(b) 15 cm
(c) 4 cm
(d) 8 cm
Ans: (d)
Draw OP ⊥ AB.
As perpendicular from the centre to a chord bisect the chord, so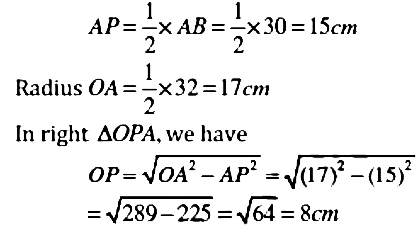
Q4: In Fig, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to: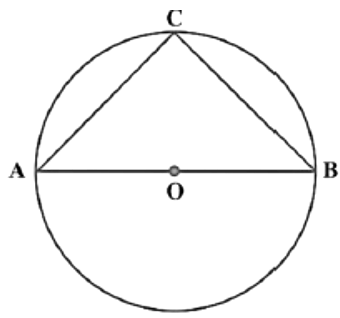 (a) 30º
(a) 30º
(b) 60º
(c) 90º
(d) 45º
Ans: (d)
As AOB is a diameter of the circle,
∠C = 90º
[∵Angles in a semi-circle is 90º]
Now, AC = BC
∠A = ∠B
[∵Angles opposite to equal sides of triangle are equal]
0 ∠A+∠B +∠C =180º
⇒2∠A+ 90º =180º
⇒ 2∠A = 90º⇒∠A = 90º ÷ 2 = 45º
Hence, (d) is the correct answer.
Q5: In Fig, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to: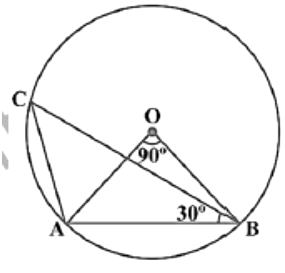
(a) 30º
(b) 45º
(c) 90º
(d) 60º
Ans: (d)
In ΔOAB, we have
OA = OB
[Radii of the same circle]
∴∠OAB = ∠OBA
∴ 2∠OAB = (180º −∠AOB)
= (180º −90º ) [∵Sum of angles of Δ is 180º]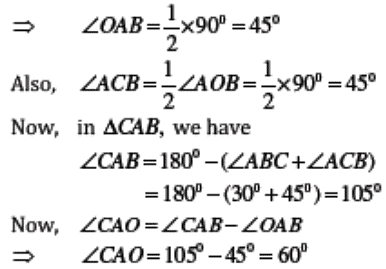
True or False
Q6: Through three collinear points a circle can be drawn.
Ans: The given statement is false because a circle through two points cannot pass through a point which is collinear to these two points.
Q7: If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
Ans: The given statement is false because there can be many points D such that ∠BDC = 60° and each such point cannot be centre of the circle through A, B, C.
Q8: Two chords AB and AC of a circle with centre O are on the opposite sides of OA.
Then ∠OAB = ∠OAC.
Ans: The given statement is false, because the angles will be equal if AB = AC.
Q9. If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2
Ans: AOB is a diameter of a circle and C is a point on the circle.
∴ ∠ACB = 90º [∵Angle in a semicircle is a right angle]
In right ΔABC,
AC2 + BC2 = AB2 [By Pythagoras theorem]
Hence, the given statement is true.
|
129 videos|736 docs|84 tests
|





















