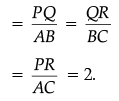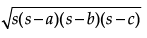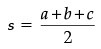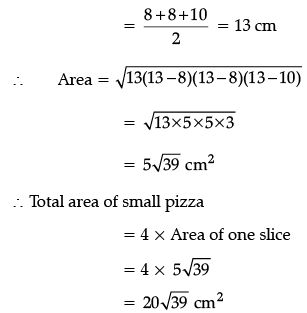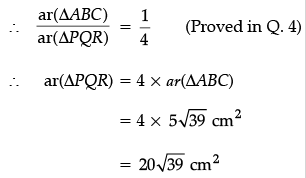Class 10 Math: CBSE Sample Question Paper- Term I (2021-22)- 2 | CBSE Sample Papers For Class 10 PDF Download
Class-X
Time: 90 Minutes
M.M: 40
General Instructions:
- The question paper contains three parts A, B and C.
- Section A consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section B consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
Section - A
Q.1: The product of two numbers is 1800 and their LCM is 200, then the HCF of the numbers is:
(a) 9
(b) 90
(c) 900
(d) 360000
Correct Answer is Option (a)
HCF = Product of two numbers/LCM
= 1800/200
= 9.
Q.2: If α and β are the zeroes of the quadratic polynomial f(x) = kx2 + 4x + 4, then the value of α+β/αβ is:
(a) 2/3
(b) 1
(c) – 1
(d) – 2
Correct Answer is Option (c)
It is given that,
f(x) = kx2 + 4x + 4
∴ α + β = − 4/kand αβ = 4/k
∴ α+β/αβ = -4/k/4/k
= -1
Q.3: The value of k for which the system of equations kx + 10y = k – 5 and 10x + ky = k will have infinite many solutions is:
(a) – 3
(b) ± 10
(c) ± 6
(d) 4
Correct Answer is Option (b)
Here,
The system will have infinite solutions if
Then, k/10 = 10/k
⇒ k2 = 100
⇒ k = ± 10
Q.4: A box contains 80 discs, numbered from 1 to 90. If one disc is drawn at random from the box, the probability that it bears a prime number less than 30, is:
(a) 1/8
(b) 9/80
(c) 11/80
(d) 3/20
Correct Answer is Option (a)
Total number outcomes = 80
i.e., n(S) = 80
Prime number less than 30 = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
i.e., n(E) = 10
∴ Required probability,
P(E) = n(E)/n(S)
= 10/80
= 1/8
Q.5: The area of circle that can be inscribed in a square of side 2.8 cm, is:
(a) 6.60 cm2
(b) 6.08 cm2
(c) 6.76 cm2
(d) 6.16 cm2
Correct Answer is Option (d)
Since, side of a square = diameter of the circle
∴ Radius of the circle (r) = 2.8/2= 1.4 cm
Now, area of the circle = πr2
= 22/7 x 1.4 x 1.4
= 6.16 cm2.
Q.6: The largest number which divides 377,286 and 421 leaving remainders 9, 10 and 7 respectively, is:
(a) 23
(b) 46
(c) 69
(d) 92
Correct Answer is Option (b)
Required number
= 377 – 9 i.e., 368
286 – 10 i.e., 276 and 421 – 7 i.e., 414
368 = 24 × 23
276 = 22 × 3 × 23
and 414 = 2 × 32 × 23
Hence, HCF = 2 × 23
= 46.
Q.7: If 2 sin θ – √3 = 0, then the value of 4 cos3 θ – 3 cos θ is:
(a) – 1
(b) 1
(c) 2
(d) 4
Correct Answer is Option (a)
2 sin θ − √3 = 0
⇒ sin θ = √3/2
⇒ sin θ = sin 60°
⇒ θ = 60°
Now, 4 cos3 θ – 3cos θ
= 4(cos 60°)3 – 3 cos 60°
= 4(cos 60°)3 – 3 cos 60°= -1
Q.8: In DABC, DE || BC, then the value of x is:
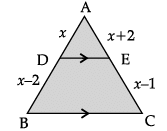
(a) 1 unit
(b) 2 unit
(c) 3 unit
(d) 4 unit
Correct Answer is Option (d)
Since, DE || BC, then
AD/DB = AE/EC
⇒ x/x-2 = x + 2/x - 1
⇒ x(x - 1) = x2 - 4
⇒ x2 - x = x2 - 4
⇒ x = 4 Unit
Q.9: The number 0.131313 ______ is the form of p/q will be equal:
(a) 4/11
(b) 2/11
(c) 13/99
(d) 2/33
Correct Answer is Option (c)
0.131313 ........ =
So,= 13/99
Q.10: The pair of linear equations 3x + 6 = 10y and 2x – 15y + 3 = 0 is:
(a) inconsistent
(b) consistent
(c) parallel
(d) none of these
Correct Answer is Option (b)
Here,
∴ The given system of linear equations is consistent.
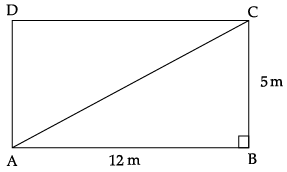
Q.11: Riya was drawing a rectangle on her worksheet, then length of diagonal of a rectangle having length 12 m and breadth 5 cm is:
(a) 13 m
(b) 12 cm
(c) 5 m
(d) 10 cm
Correct Answer is Option (a)
Let ABCD be a rectangle, then, AB = 12 m and BC = 5 cm in right angled DABC,
AC2 = AB2 + BC2
(By using Pythagoras Theorem)
= (12)2 + (5)2
= 144 + 25
= 169
∴ AC = √169 = 13 m.
Q.12: While playing with circular toy. Mohit, started measuring it, if he measured perimeter of a sector of a circle of radius 4 cm is 20 cm, then the arc ACB is: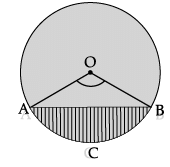
(a) 8 cm
(b) 28 cm
(c) 12 cm
(d) 8.5 cm
Correct Answer is Option (c)
Here OACB is a sector of circle
and OA= OB = 4 cm
∴ Perimeter = 20 cm (given)
OA+ OB +arc ACB = 20
⇒ 4 + 4 + arc ACB = 20
⇒ arc ACB = (20 – 8) cm
⇒ 12 cm
Q.13: The value of 4 sin2 30° + cosec2 30° + 3 cos 0° + 4 sin 90° – tan2 60° is:
(a) 9
(b) 10
(c) 11
(d) 12
Correct Answer is Option (a)
4 sin2 30° + cosec2 30° + 3 cos 0° + 4 sin 90° – tan2 60°.
= 4(1/2)2 + (2)2 + 3 x 1 + 4 x 1 - (√3)2
= 4 x 1/4 + 4 + 7 - 3
= 1 + 4 + 4= 9.
Q.14: The decimal expansions of 17/54 × 23 is:
(a) 0.034
(b) 0.3040
(c) 0.0034
(d) 0.3440
Correct Answer is Option (c)
= 34/10000
= 0.0034
Q.15: In the given figure, ΔABC ~ ΔADE. If AB = 8 cm, DE = 4.5 cm and BC = 9 cm, then AE is:
(a) 4.5 cm
(b) 4 cm
(c) 3.8 cm
(d) 4.8 cm
Correct Answer is Option (b)
We have, ΔABC ~ DADE
⇒ AB/AE = BC/DE
⇒ 8/AE = 9/4.5⇒ AE = 8 x 4.5/9
= 4 cm
Q.16: A letter is chosen at random from the letters of the word 'MATHEMATICS' then the probability that the chosen letter is a vowel; is:
(a) 4/11
(b) 7/11
(c) 1
(d) 0
Correct Answer is Option (a)
Total no. of letters in the given word = 11
i.e., n(S) = 11
and no. of vowels in the given word = 4
i.e., n(E) = 4
∴ P(choosing a vowel) = 4/11.
Q.17: If three vertices of a triangle are (2, 4), (5, 7) and (3, 7), then its centroid is:
(a) (3, 6)
(b) (10/3, 6)
(c) ( 11/3, 17/3)
(d) ( 10/3, 6)
Correct Answer is Option (b)
Centroid of a triangle
Q.18: If x = a sin θ and y = b cos θ, then the value of b2x2 + a2y2 is:
(a) ab
(b) 1
(c) a2b2
(d) a2 + b2
Correct Answer is Option (c)
We have,
x = α sin θ
and y = b cos θ
Then, b2x2 + a2y2 = b2 × a2 sin2 q + a2 × b2 cos2 θ
= a2b2 (sin2 θ + cos2 θ)
= a2b2 × 1
[∵ sin2 θ + cos2 θ = 1]
= a2b2.
Q.19: If the numbers are 2, 2, 2, 3, 3, 5, 5, 7, 7, 7, 7, 9, 9, 9 given and one number is selected at random, then the probability (getting 7) is:
(a) 3/14
(b) 1/7
(c) 2/7
(d) 3/7
Correct Answer is Option (c)
Total outcome,
n(S) = 14
Favourable outcomes,
n(E) = 4
∴ (getting 7) = n(E)/n(S)
= 4/14
= 2/7
Q.20: If the points A(5, – 3), B(– 6, – 3), C(8, 4) and D(k, 5) are the vertices of a parallelogram, taken in order, then the value of k is:
(a) 17
(b) 18
(c) 19
(d) 10
Correct Answer is Option (c)
In parallelogram, Mid point of AC = Mid Point of BD
⇒ k – 6 = 13
⇒ k = 19.
Section - B
Q.21: If sum of two numbers is 1215 and their HCF is 81, then the possible number of pairs of such numbers are
(a) 2
(b) 3
(c) 4
(d) 5
Correct Answer is Option (c)
Since HCF = 81, two numbers can be taken as 81x and 81y,
ATQ 81x + 81y = 1215
Or x + y = 15
which gives four co prime pairs
(1,14), (2,13), (4,11), (7, 8)
Q.22. Given below is the graph representing two linear equations by lines AB and CD respectively. What is the area of the triangle formed by these two lines and the line x = 0?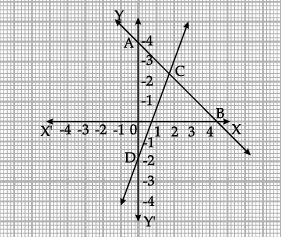
(a) 3sq. units
(b) 4sq. units
(c) 6sq. units
(d) 8sq. units
Correct Answer is Option (c)
Required Area is area of triangle
ACD = 1/2× 6×2= 6 sq units
Q.23: If tan α + cot α = 2, then tan20α + cot20α =
(a) 0
(b) 2
(c) 20
(d) 220
Correct Answer is Option (b)
tan α + cot α = 2
gives α = 45°.
So tan α = cot α = 1
tan20α + cot20α = 120 + 120 = 1+1 = 2
Q.24: If 217x + 131y = 913, 131x + 217y = 827, then x + y is
(a) 5
(b) 6
(c) 7
(d) 8
Correct Answer is Option (c)
Adding the two given equations we get:
348x + 348y = 1740.
So x + y = 5
Q.25: The LCM of two prime numbers p and q (p > q) is 221. Find the value of 3p – q.
(a) 4
(b) 28
(c) 38
(d) 48
Correct Answer is Option (c)
LCM of two prime numbers = product of the numbers
221 = 13 × 17.
So p = 17 & q = 13
∴ 3p – q = 51-13 = 38
Q.26: A card is drawn from a well shuffled deck of cards. What is the probability that the card drawn is neither a king nor a queen?
(a) 11/13
(b) 12/13
(c) 11/26
(d) 11/52
Correct Answer is Option (a)
Probability that the card drawn is neither a king nor a queen
= 52 - 8/52
= 44/52 = 11/13
Q.27: Two fair dice are rolled simultaneously. The probability that 5 will come up at least once is
(a) 5/36
(b) 11/36
(c) 12/36
(d) 23/36
Correct Answer is Option (b)
Outcomes when 5 will come up at least once are(1,5), (2,5), (3,5), (4,5), (5,5), (6,5), (5,1), (5,2), (5,3), (5,4) and (5,6) Probability that 5 will come up at least once = 11/36
Q.28: If 1+ sin2α = 3 sinα cosα, then values of cot α are
(a) –1, 1
(b) 0,1
(c) 1, 2
(d) –1, –1
Correct Answer is Option (c)
1+ sin2α = 3 sinα cos α
sin2α + cos2α + sin2α = 3 sinα cos α
2 sin2α – 3sinα cos α + cos2α = 0
(2sinα – cos α)(sinα– cosα) =0
∴ cotα = 2 or cotα = 1
Q.29: The vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6) and D(3, 5). Then (x, y) is
(a) (6, 3)
(b) (3, 6)
(c) (5, 6)
(d) (1, 4)
Correct Answer is Option (a)
Since ABCD is a parallelogram, diagonals AC and BD bisect each other,
∴ mid point of AC= mid point of BD
Comparing the co-ordinates, we get,
∴ (x, y) = (6, 3)
Q.30: In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is
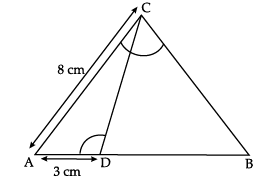
(a) 22/3 cm
(b) 26/3 cm
(c) 55/3 cm
(d) 64/3 cm
Correct Answer is Option (c)
ΔACD ~ Δ ABC(AA)
8/AB = 3/8
This gives AB = 64/3 cm.
So BD = AB – AD = 64/3 – 3 = 55/3cm.
Q.31: The equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is 1
(a) 2x – y +7 = 0
(b) 3x + 2y – 7 = 0
(c) 3x – y – 7 = 0
(d) 3x + y – 7 = 0
Correct Answer is Option (c)
Any point (x, y) of perpendicular bisector will be equidistant from A & B.
Solving we get, –12x – 4y + 28 = 0
or 3x + y – 7 = 0
Q.32: In the given figure, D is the mid-point of BC, then the value of cot y°/cot x° is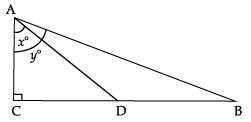
(a) 2
(b) 1/2
(c) 1/3
(d) 1/4
Correct Answer is Option (b)
Q.33: The smallest number by which 1/13 should be multiplied so that its decimal expansion terminates after two decimal places is
(a) 13/100
(b) 13/10
(c) 10/13
(d) 100/13
Correct Answer is Option (a)
The smallest number by which 1/13 should be multiplied so that its decimal expansion terminates after two decimal points is 13/100 as
13/100
Q.34: Sides AB and BE of a right triangle, right angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is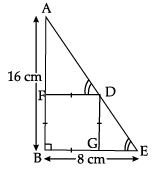
(a) 32/3cm
(b) 16/3cm
(c) 8/3cm
(d) 4/3cm
Correct Answer is Option (b)
ΔABE is a right triangle & FDGB is a square of side x cm ΔAFD ~Δ DGE(AA)
128 = 24x or x = 16/3cm
Q.35: Point P divides the line segment joining R(–1, 3) and S(9, 8) in ratio k :1. If P lies on the line x – y + 2 = 0, then value of k is
(a) 2/3
(b) 1/2
(c) 1/3
(d) 1/4
Correct Answer is Option (a)
Since P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1
∴ coordinates of P are
Since P lies on the line x – y + 2 = 0, then
9k –1 –8k–3 +2k+2 = 0
which gives k = 2/3
Q.36: In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is
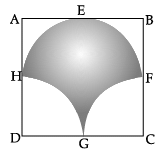
(a) 44 cm²
(b) 49 cm²
(c) 98 cm²
(d) 49π/2 cm²
Correct Answer is Option (c)
Shaded area = Area of semicircle + (Area of half square – Area of two quadrants) = Area of semicircle +(Area of half square – Area of semicircle) = Area of half square= 1/2 × 14 ×14 = 98cm²
Q.37: Given below is the picture of the Olympic rings made by taking five congruent circles of radius 1 cm each, intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1 cm. Total area of all the dotted regions assuming the thickness of the rings to be negligible is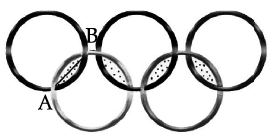
(a) 4(π/12 – √3/4) cm²
(b) (π/6 – √3/4) cm²
(c) 4(π/6 – √3/4) cm²
(d) 8(π/6 – √3/4) cm²
Correct Answer is Option (d)
Let O be the center of the circle.
OA = OB = AB = 1cm.
So ΔDAB is an equilateral triangle and
∴ ∠AOB Required Area = 8x Area of one segment with r = 1cm, q = 60°
= 8(π/6 – √3 /4)cm²
Q.38: If 2 and 1/2 are the zeros of px2 + 5x + r, then
(a) p = r = 2
(b) p = r = – 2
(c) p = 2, r = – 2
(d) p = – 2, r = 2
Correct Answer is Option (b)
Sum of zeroes = 2 + 1/2 = –5/p
i.e. 5/2 = –5/p. So p = –2
Product of zeroes = 2 x 1/2 = r/p
i.e. r/p = 1 or r = p = –2
Q.39: The circumference of a circle is 100 cm. The side of a square inscribed in the circle is
(A) 50√2 cm
(B) 100/π cm
(C) 50√2 /π cm
(D) 100√2/π cm
Correct Answer is Option (c)
2πr = 100.
So, Diameter = 2r =100/π = diagonal of the square. side √2 = diagonal of square = 100√2 π
∴ side = 100√2 π = 50√2/π
Q.40: The number of solutions of 3x+y = 243 and 243x–y = 3 is
(A) 0
(B) 1
(C) 2
(D) infinite
Correct Answer is Option (b)
3x+y = 243 = 35
So x + y = 5 (1)
243x–y = 3
(35)x–y = 31
So 5x–5y = 1
Since,so unique Solution.
Section - C
Q. 41 to 45 are based on Case Study - 1
Read the following text and answer the following questions on the basis of the same: The four angles of a cyclic quadrilateral ABCD are given in the following figure: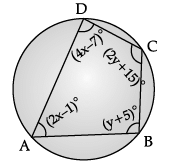
Q.41: The value of x is:
(a) 11
(b) 22
(c) 33
(d) 50
Correct Answer is Option (c)
As we know, ∠A + ∠C = 180°
⇒ 2x – 1 + 2y + 15 = 180°
⇒ x + y = 83 ...(i)
∠B + ∠D = 180°y + 5 + 4x – 7 = 180°
4x + y = 182 ...(ii)
Subtracting eq. (i) from (ii), we get
3x = 99
⇒ x = 33.
Q.42: The value of (∠A + ∠D) is:
(a) 180°
(b) 190°
(c) 200°
(d) 150°
Correct Answer is Option (b)
∠A + ∠D = (2x – 1)° + (4x – 7)°
= (6x – 8)°
= (6 × 33 – 8)°
[From question (i), x = 33]
Q.43: The value of y is:
(a) 25
(b) 30
(c) 40
(d) 50
Correct Answer is Option (d)
From question (1),
Putting x = 33 is eq. (i),
we get 33 + y = 83
⇒ y = 83 – 33 = 50.
Q.44: The measure of ∠D is:
(a) 120°
(b) 115°
(c) 125°
(d) 95°
Correct Answer is Option (c)
∠D = (4x – 7)°
= (4 × 33 – 7)°
= 125°.
Q.45: The measure of (∠B + ∠C) is:
(a) 170°
(b) 150°
(c) 190°
(d) 180°
Correct Answer is Option (a)
∠B + ∠C = (y + 5)° + (2y + 15)°
= (3y + 20)°
= (3 × 50° + 20°)
= 170°.
Q.46 to 50 are based on case Study - 2
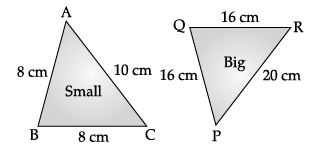
One small size and another big size pizza was ordered by Mr. Rohan for a breakfast. Instead of eating this he sit to compare the slices of the pizza and then many questions came into his mind. The size of the slice of small and big pizza is shown in below figure.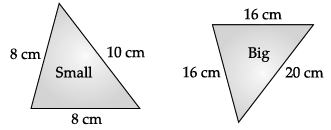
Q.46: The slices of smaller pizza and bigger pizza are similar using:
(a) AA criterian
(b) SAS rule
(c) SSS rule
(d) slices are not similar.
Correct Answer is Option (c)
Let ABC and PQR represent the slice of smaller and bigger pizza, then in DABC and DPQR,
Q.47: The scale factor is:
(a) 1
(b) 2
(c) 3
(d) 4
Correct Answer is Option (b)
When two triangles are similar the reduced ratio of any two corresponding sides is called the scale factor, so scale factor
Q.48: If the small pizza has cut into 4 slices, then what will be the total area of the pizza ?
(a) 39 cm2
(b) 20√39 cm2
(c) 5√39 cm2
(d) 40 cm2
Correct Answer is Option (a)
By using Heron's formula,
area of DABC =
then
Q.49: The ratio of area of small slices to bigger slice is:
(a) 1 : 4
(b) 1 : 8
(c) 1 : 16
(d) 1 : 2
Correct Answer is Option (a)
Q.50: If the bigger pizza has cut into 3 slices, then the total area of bigger pizza is:
(a) 60 cm2
(b) 20√39 cm2
(c) 539 cm2
(d) 60√39 cm2
Correct Answer is Option (a)
Now, total area of bigger pizza
= 3 × area of one slice
= 3 × 20√39 cm2
= 60√39 cm2
|
303 docs|7 tests
|
FAQs on Class 10 Math: CBSE Sample Question Paper- Term I (2021-22)- 2 - CBSE Sample Papers For Class 10
| 1. How much time is allocated for the Class 10 Math exam? |  |
| 2. What is the maximum marks for the Class 10 Math exam? |  |
| 3. What is the format of the Class 10 Math exam? |  |
| 4. How can I prepare for the Class 10 Math exam? |  |
| 5. Are there any specific topics or chapters that are important for the Class 10 Math exam? |  |

|
Explore Courses for Class 10 exam
|

|
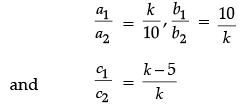
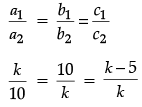
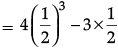 = -1
= -1
 = 13/99
= 13/99
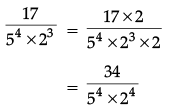
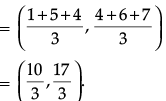
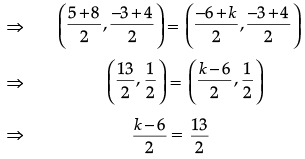
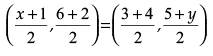
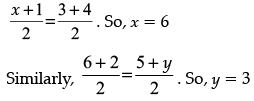
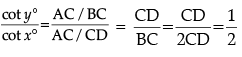

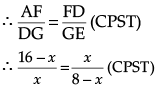
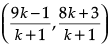

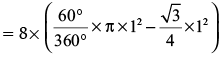
 so unique Solution.
so unique Solution.