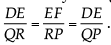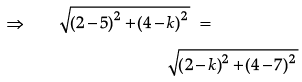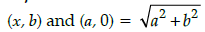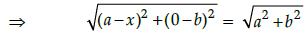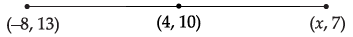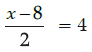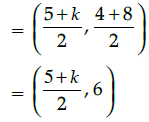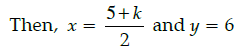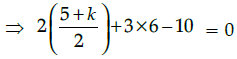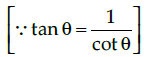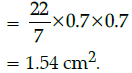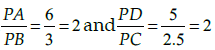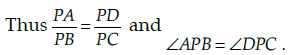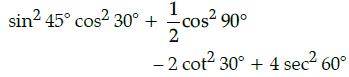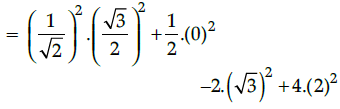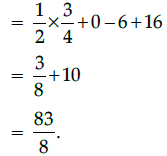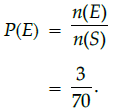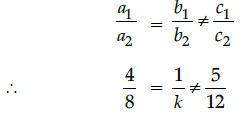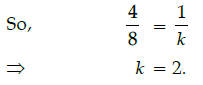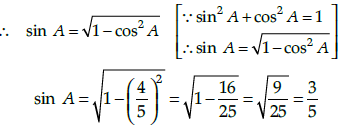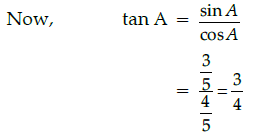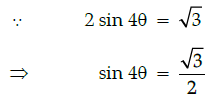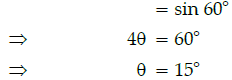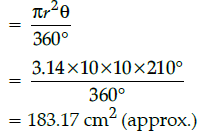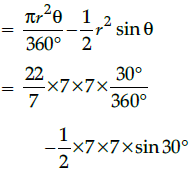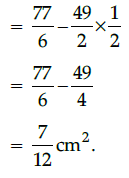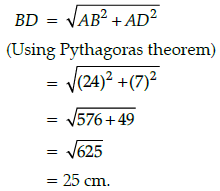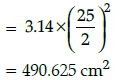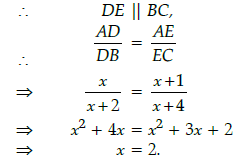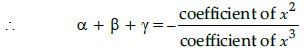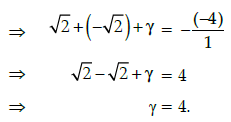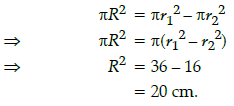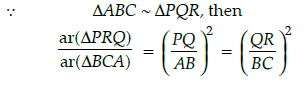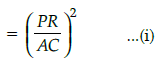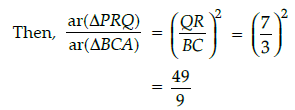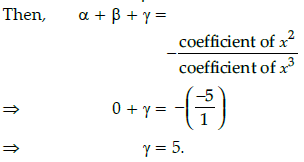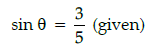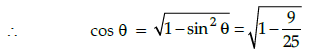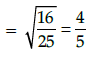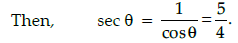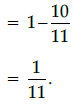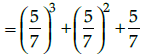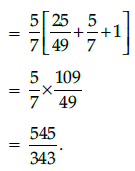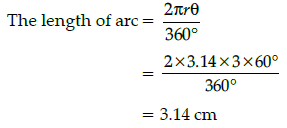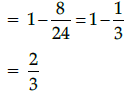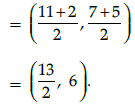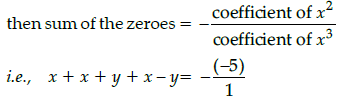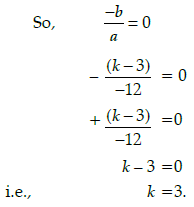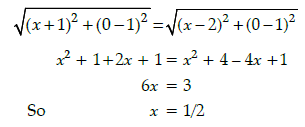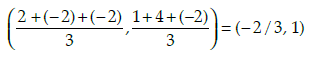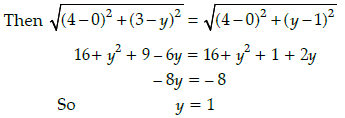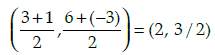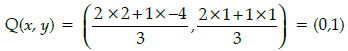Class 10 Mathematics: CBSE Sample Question Paper- Term I (2021-22) - 1 | Mathematics (Maths) Class 10 PDF Download
Class-X
Time: 90 Minutes
M.M: 40
General Instructions:
- The question paper contains three parts A, B and C.
- Section A consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section B consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
Section - A
Q.1: The smallest number which when divided by 26 and 32 leaves remainders 6 and 12 respectively is:
(a) 416
(b) 420
(c) 396
(d) 436
Correct Answer is Option (c)
∵ 26 – 6 = 20 and 32 – 12 = 20
Now, 26 = 2 × 13 and 32 = 2 × 2 × 2 × 2 × 2∴ LCM (26, 32) = 25 × 13 = 416
Required number = LCM (26, 32) – 20 = 416 – 20
= 396.
Q.2: If in two triangles DEF and PQR, ∠D = ∠Q and∠R = ∠E, then which of the following is not true?
(a) 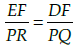
(b) 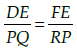
(c) 
(d) 
Correct Answer is Option (b)
In ΔDEF and ΔPQR, ∠D = ∠Q and ∠R = ∠E. By AA similarity,
we get ΔDEF ~ ΔQRP.
Hence,
Q.3: If the points P(2, 4) is equidistant from the points A(5, k) and B(k, 7), then the value of k is:
(a) 3
(b) 2
(c) 1
(d) – 3
Correct Answer is Option (a)
Distance of AP = Distance of BP
⇒ (– 3)2 + (4 – k)2 = (2 – k)2 + (– 3)2
⇒ 16 + k2 – 8k = 4 + k2 – 4k
⇒ –4k = –12
⇒ k = 3.
Q.4: If 3x + y = 14 and 2x – y = 1, then the value of y is:
(a) 2
(b) 3
(c) 4
(d) 5
Correct Answer is Option (d)
3x + y = 14 ...(i)
and 2x – y = 1 ...(i)
On adding, 5x = 15
⇒ x = 3
Putting x = 3 in eq. (i), we get
9 + y = 14
⇒ y = 14 – 9 = 5.
Q.5: If the distance between the points (x, b) and (a, 0) is 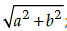 then the value of x is:
then the value of x is:
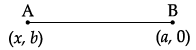 (a) a
(a) a
(b) b
(c) 2a
(d) 2b
Correct Answer is Option (c)
Distance between the points
⇒ (a – x)2 + b = a2 + b2
⇒ a2 + x2 – 2ax = a2
⇒ x2 – 2ax = 0
⇒ x(x – 2a) = 0
⇒ x = 0, 2a.
Q.6: In the equation 2x + 3y = 13, if x is having a value 2, then corresponding value of y is
(a) 2
(b) 3
(c) 1
(d) 4
Correct Answer is Option (b)
Putting x = 2 in equation
2x + 3y = 13, we get
2 × 2 + 3y = 13
⇒ 3y = 13 – 4 = 9
⇒ y = 3.
Q.7: If (4, 10) is the mid point of the line segment joining (– 8, 13) and (x, 7), then x is equal to:
(a) 16
(b) 10
(c) 8
(d) 4
Correct Answer is Option (a)
Here, x1 = – 8, y1 = 13
and x2 = x, y2 = 7
Comparing both sides, we get
⇒ x – 8 = 8
i.e., x = 16.
Q.8: If the mid point of the line segment joining the points A(5, 4) and B(k, 8) is P(x, y) and 2x + 3y – 10 = 0, then the value of k is:
(a) 12
(b) – 12
(c) 13
(d) – 13
Correct Answer is Option (d)
Mid point of A (5, 4) and B(k, 8)
which is equal to P(x, y)
∵ 2x + 3y – 10 = 0⇒ 5 + k + 8 = 0
⇒ k = – 13.
Q.9: Aman and Nitin are two friends. One day, they discuss about different concepts of circles and squares. And they try to solve the problem which is given below :
If the perimeter of a circle is equal to that of a square, then the ratio of their areas is:
(a) 22 : 7
(b) 14 : 11
(c) 7 : 22
(d) 11 : 14
Correct Answer is Option (b)
Let the radius of circle be ‘r’ and side of square be ‘a’.
According to given question,
Perimeter of circle = Perimeter of square
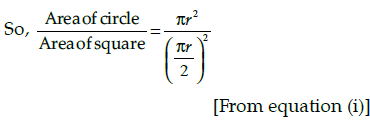
Solving equation (i), we get result as 14/11.
Q.10: If tan θ + cot θ = 7, then the value of tan2 θ + cot2 θ is:
(a) 48
(b) 49
(c) 47
(d) 46
Correct Answer is Option (a)
Given,
tan θ + cot θ = 7
Taking square on both sides, we get
tan2θ + cot2θ + 2 tan θ . cot θ = 49
⇒ tan2θ + cot2θ + 2 = 49
⇒ tan2 θ + cot2 θ = 49 – 2 = 47.
Q.11: The area of circle that can be inscribed in a square of side 1.4 cm, is:
(a) 2.2 cm
(b) 1.82 cm
(c) 1.62 cm
(d) 1.54 cm2
Correct Answer is Option (d)
side of a square = diameter of the circle
∴ Radius of the circle (r) = 1.4/2
= 0.7 cm
Now, area of the circle = πr2
Q.12: In the figure given below, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to: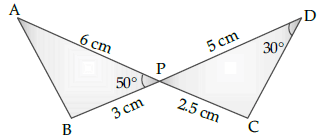
(a) 50°
(b) 30°
(c) 60°
(d) 100°
Correct Answer is Option (d)
In the given figure
By SAS similarity, we get ΔAPB ~ ΔDPC.Hence, ∠PBA = 100°.
Q.13: The value of sin2 45° cos2 30° + 1/2 cos2 90° – 2 cot2 30° + 4 sec2 60°.
(a) 83/8
(b) 83/7
(c) 81/8
(d) 83/5
Correct Answer is Option (a)
Q.14: A box contains cards numbered 1 to 70. A card is drawn at random from the box. The probability that the drawn card has a number which is a perfect cube is:
(a) 1/7
(b) 2/35
(c) 1/14
(d) 3/70
Correct Answer is Option (d)
Given numbers = 1, 2, 3, 4, 5, ...., 70
i.e., total outcomes,
n(S) = 70
Perfect cube numbers between 1 to 70 = 8, 27, 64
i.e., favourable outcomes,
n(E) = 3∴ Required probability,
Q.15: The value of k for which the system of equations 4x + y = 5 and 8x + ky = 12 has not solution, is:
(a) 10
(b) 5
(c) 2
(d) 1
Correct Answer is Option ()
System has no solution if
Q.16: If cos A =4/5 then the value of tan A is:
(a) 3/5
(b) 3/4
(c) 4/3
(d) 1/8
Correct Answer is Option (b)
Given, cos A =4/5
Q.17: If 2 sin 4θ = 1/2, then the value of θ is :
(a) 15º
(b) 36º
(c) 45º
(d) 60º
Correct Answer is Option (a)
Q.18: Rahul is a class X student, he love to play with marbles. He has a bag containing 10 blue, 7 white and 8 red marbles. He thought that, he will win game only when he draw white marble. Then what will be the probability that he will win the game.
(a) 17/25
(b) 18/25
(c) 3/5
(d) 11/25
Correct Answer is Option (b)
Total number of marbles
= 10 + 7 + 8
= 25
i.e., n(S) = 25
Number of non-white marbles
= 10 + 8 + 18
i.e., n(E) = 18
P(getting a non white marble)
Q.19: If the length of the minute hand of a clock is 10 cm, then the area swept by the minute hand from 9.10 a.m. to 9.45 a.m., is:
(a) 183.17 cm2
(b) 184.17 cm2
(c) 182.17 cm2
(d) 185.17 cm2
Correct Answer is Option (a)
Since, angle subtended in 1 minute = 6°
So, angle subtended in 35 minutes
= 35 × 6°
= 210°
Now, area swept by the minute hand = area of the sector
Q.20: The area of minor segment of a circle of radius 7 cm, when its central angle is 30, is:
(a) 5/12 cm2
(b) 1/2 cm2
(c) 7/12 cm2
(d) 11/12 cm2
Correct Answer is Option (c)
Given, r = 7 cm and q = 30°
Then, the area of minor segment
Section - B
Q.21: In the given figure, if ABCD is a rectangle, then area of the circle is :
[Using, π = 3.14]
(a) 492 cm2
(b) 492.625 cm2
(c) 432.625 cm2
(d) 490.625 cm2
Correct Answer is Option (a)
Here, AB = 24 cm and AD = 7 cm.
and BD is a diagonal of rectangle ABCD
In DBAD,
∵ Diameter of the circle = Diagonal BD of ABCDi.e., 2r = 25
⇒ r = 25/2 cm
Area of the circle = πr2
Q.22: If 2x – y = 4, y – z = 6 and x – z = 10, then x is :
(a) – 4
(b) 3
(c) 0
(d) 4
Correct Answer is Option (c)
2x – y = 4 ...(i)
y – z = 6 ...(ii)
and x – z = 10 ...(iii)
From eq. (ii), we get
z = y – 6
Putting the value of z in eq. (iii), we get
x – y = 4 ...(iv)
Solving eq. (i) and (iv), we get
x = 0 and y = – 4
Q.23: In DABC, if DE || BC, then the value of x is :
(a) 1
(b) 2
(c) 3
(d) 4
Correct Answer is Option (b)
Q.24: If two zeroes of the polynomial p(x) = x3 – 4x2 – 3x + 12 are √2 and −√2, then its third zero is:
(a) 4
(b) 5
(c) 6
(d) 1
Correct Answer is Option (a)
Let α, β and γ are zeroes
of given polynomial, then α = √2 and β = − √2
Q.25: The square of radius of a circle whose area is equal to the difference of the areas of the two circlces of radii 6 cm and 4 cm is:
(a) 16π cm
(b) 20 cm
(c) 8π cm
(d) 2π cm
Correct Answer is Option (b)
Let r1 = 6 cm
and r2 = 4 cm.
According to question,
Area of circle = area of first circle – area of second circle.
Q.26: It is given that DABC ~ DPQR with 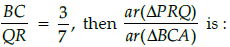
(a) 49/9
(b) 49/4
(c) 47/4
(d) 47/9
Correct Answer is Option (a)
Q.27: If two zeroes of the polynomial p(x) = x3 – 5x2 – 16x + 80 are equal in magnitude but opposite in sign, then third zero is :
(a) 5
(b) 3
(c) –2
(d) 4
Correct Answer is Option (a)
Let α, β and γ be the zeroes of given polynomial
p(x) = x3 – 5x2 – 16x + 80, such that α+ β = 0
Q.28: If sin θ =3/5, then the value of sec q is:
(a) 4/5
(b) 3/4
(c) 1/5
(d) 5/4
Correct Answer is Option (d)
Q.29: If E be an event such that P(E) = 10/11 , then P(not E) =
(a) 10/11
(b) 11/10
(c) 1/11
(d) 1/10
Correct Answer is Option (c)
Given P(E) = 10/11
So, P(not E) = 1 – P(E)
Q.30: If 5 cosec θ = 7, then the value of sin3 θ + sin2 θ + sin θ is:
(a) 109/343
(b) 545/343
(c) 107/343
(d) 113/343
Correct Answer is Option (b)
∵ 5 cosec θ = 7 (given)
⇒ cosec θ =7/5
or sin θ = 5/7
Now, sin3 θ + sin2 θ + sin θ
Q.31: The HCF of 1500, 2500 and 3000 is:
(a) 600
(b) 500
(c) 800
(d) 400
Correct Answer is Option (b)
In case of assertion:
1500 = 22 × 3 × 53
2500 = 22 × 54
3000 = 23 × 3 × 53
HCF (1500, 2500 and 3000)
= 22 × 53
= 500
Q.32: If radius of a circle is 3 cm and of angle 60° at the centre, then the length of the arc is:
(a) 3.14 cm
(b) 6.28 cm
(c) 31.4 cm
(d) 62.8 cm
Correct Answer is Option (a)
Here, r = 3 cm and q = 60°.
Q.33: The greatest number of four digits exactly divisible by 15, 20 and 30 is :
(a) 9950
(b) 9940
(c) 9960
(d) 9970
Correct Answer is Option (c)
LCM of 15, 20 and 30 is 60 and the largest 4
digit number is 9999,
which divides by 60, get remainder 39.
So, the required number = 9999 – 39 = 9960.
Q.34: In a lottery, there are 8 prizes and 16 blanks, then the probability of not getting a prize is:
(a) 1/3
(b) 2/3
(c) 1
(d) 0
Correct Answer is Option (b)
Total Possible outcomes = 8 + 16 = 24.
No. of prizes = 8
∴ Probability (getting not a prize)
Q.35: If P(5, 3), Q(11, 5) and R(2, 7) be the vertices of DPQR and PT is a median, then the coordinates of T are:
(a) 
(b) 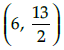
(c) (3,4)
(d) 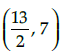
Correct Answer is Option (a)
Since PT is a median, then T is the mid point of QR.
∴ Coordinates of T are
Q.36: If the zeroes of the polynomial p(x) = x3 – 5x2 + 2x + 3 are x, x + y and x – y,
then the value of x is:
(a) 1/3
(b) 2/3
(c) 5/3
(d) 4/3
Correct Answer is Option (c)
Since x, x + y and x – y are zeroes of p(x).
∴ 3x = 5
⇒ x= 5/3
Q.37: If AB =9 cm, BC = 6 cm then AB2 + BC2 is:
(a) 115
(b) 118
(c) 117
(d) 121
Correct Answer is Option ()
Given, AB = 9 cm
and BC = 6 cm
Then, AB2 + BC2 = (9)2 + (6)2
= 81 + 36 = 117
Q.38: 3 group of children decided to calculate the length of park model designed by them for school project. The given below figure is as shown then what is the value of x ?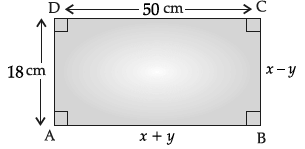
(a) 35 cm
(b) 36 cm
(c) 37 cm
(d) 34 cm
Correct Answer is Option (d)
Since ABCD is a rectangle,
AB = CD
i.e., x + y = 50 ...(i)
and BC = AD
i.e., x – y = 18 ...(ii)
On adding eq. (i) and (ii), we get
2x = 68
⇒ x = 34 cm.
Q.39: If √3 is an irrational number, then 5√3 is a/an:
(a) rational number
(b) prime number
(c) odd number
(d) irrational number
Correct Answer is Option (a)
5√3 is not a rational number because the product of rational and irrational number is irrational
Q.40: If sin θ + cos θ = √3, then the value of sin θ cos θ is:
(a) 1
(b) - 1
(c) 2
(d) 3
Correct Answer is Option (c)
Given sin θ + cos θ = √3On squaring both the sides, we get
sin2 θ + cos2 θ + 2 sin θ cos θ = 3
⇒ 1 + 2 sin θ cos θ = 3
⇒ 2 sin θ cos θ = 2
⇒ sin θ cos θ = 1.
Section - C
Case Study - 1
The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola.
Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time ‘t’ in seconds is given by the polynomial h(t) such that h(t) = –16t² + 8t + k.
Q.41: Rita’s height (in feet) above the water level is given by another polynomial p(t) with zeroes –1 and 2. Then p(t) is given by-
(a) t² + t – 2
(b) t² + 2t – 1
(c) 24t² – 24t + 48
(d) – 24t² + 24t + 48
Correct Answer is Option (d)
t= –1 & t=2 are the two zeroes of the polynomial p(t)
Then p(t)=k (t– (–1))(t–2) = k(t +1)(t–2)
When t = 0 (initially) h1 = 48ft
p(0)=k(02– 0 –2)= 48
i.e. –2k = 48
So the polynomial is -24(t²- t -2) = -24t² + 24t + 48.
Q.42: The zeroes of the polynomial r(t) = – 12t² + (k – 3)t + 48 are negative of each other. Then k is
(a) 3
(b) 0
(c) – 1.5
(d) – 3
Correct Answer is Option (a)
When the zeros are negative of each other,
sum of the zeros = 0
Q.43: What is the value of k?
(a) 0
(b) – 48
(c) 48
(d) 48/–16
Correct Answer is Option (c)
Initially, at t=0, Annie’s height is 48ft
So, at t =0, h should be equal to 48
h(0) = –16(0)² + 8(0) + k = 48
So k = 48
Q.44: A polynomial q(t) with sum of zeroes as 1 and the product as –6 is modelling Anu’s height in feet above the water at any time t( in seconds). Then q(t) is given by
(a) t² + t + 6
(b) t² + t – 6
(c) – 8t² + 8t + 48
(d) 8t² – 8t + 48
Correct Answer is Option (c)
A polynomial q(t) with sum of zeroes as 1
and the product as –6 is given by q(t) = k(t² - (sum of zeroes)t + product of zeroes)
= k(t² –1t + (–6)) ………..(1)
When t=0 (initially) q(0)= 48ft
q(0) = k(02–1 (0)–6)=48i.e. –6k = 48 or k =–8
putting k=–8 in equation (1),
required polynomial is.
=–8 (t2–1t–6)
=–8 t2 + 8t +48
Q.45: At what time will she touch the water in the pool?
(a) 30 seconds
(b) 2 seconds
(c) 1.5 seconds
(d) 0.5 seconds
Correct Answer is Option (b)
When Annie touches the pool, her height =0 feet
i.e. –16t² + 8t + 48 =0 above water level
2t² – t –6 = 0
2t² - 4t +3t -6 = 0
2t(t-2) +3(t–2) = 0
(2t +3) (t–2) = 0i.e. t = 2 or t= –3/2
Since time cannot be negative , so t = 2 seconds
Case Study - 2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf. It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground. Each team plays with 11 players on the field during the game including the goalie. Positions you might play include-
Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K
Using the picture of a hockey field below, answer the questions that follow: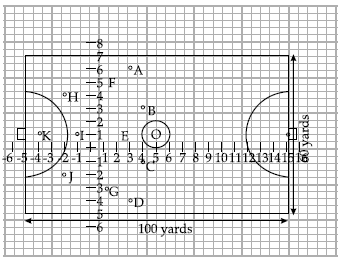
Q.46: The point on x axis equidistant from I and E is 1
(a) (1/2, 0)
(b) (0, – 1/2)
(c) (– 1/2, 0)
(d) ( 0, 1/2)
Correct Answer is Option (a)
Let the point of × axis equidistant from I (–1, 1) and E(2,1) be (x, 0)
Then
∴ The required point is (1/2, 0)
Q.47: The coordinates of the centroid of ΔEHJ are
(a) (– 2/3, 1)
(b) (1, – 2/3)
(c) (2/3, 1)
(d) ( – 2/3, – 1)
Correct Answer is Option (a)
Centroid of ΔEHJ with E(2, 1), H(–2, 4) & J(–2, –2) is
Q.48: The point on y axis equidistant from B and C is
(a) (– 1, 0)
(b) (0, – 1)
(c) (1, 0)
(d) ( 0, 1)
Correct Answer is Option ()
Let the point of y axis equidistant from B(4, 3) and C(4, – 1) be (0, y)
∴The required point is (0, 1)
Q.49: If a player P needs to be at equal distances from A and G, such that A, P and G are in straight line, then position of P will be given by
(a) (– 3/2, 2)
(b) (2, – 3/2)
(c) (2, 3/2)
(d) ( – 2, – 3)
Correct Answer is Option (c)
If P needs to be equal distance from A(3, 6) and G(1, –3), such that A, P and G are collinear, than P will be the mid-point of AG.
So coordinates of P will be
Q.50: What are the coordinates of the position of a player Q such that his distance from K is twice his distance from E and K, Q and E are collinear?
(a) (1, 0)
(b) (0, 1)
(c) (– 2, 1)
(d) (– 1, 0)
Correct Answer is Option (b)
Let the coordinates of the position of a player Q such that his distance from K(–4, 1) is twice his distance from E(2, 1) be Q(x, y)
Then KQ : QE = 2 : 1
|
127 videos|584 docs|79 tests
|