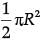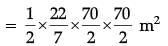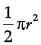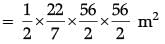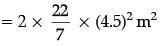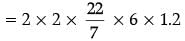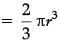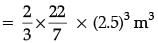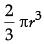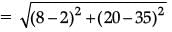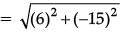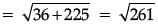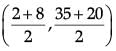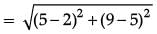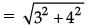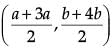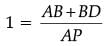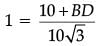Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Basic) - 2 | CBSE Sample Papers For Class 10 PDF Download
Class X
Mathematics – Basic
Sample Question Paper 2020-21
Max. Marks : 80
Duration : 3 hrs.
General Instructions :
1. This question paper contains two parts A and B.
2. Both Part A and Part B have internal choices.
Part – A
1. It consists of two sections- I and II.
2. Section I has 16 question. Internal choice is provided in 5 questions.
3. Section II has four case study-based questions. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part – B
1. Question No 21 to 26 are Very short answer Type questions of 2 marks each.
2. Question No 27 to 33 are Short Answer Type questions of 3 marks each.
3. Question No 34 to 36 are Long Answer Type questions of 5 marks each.
4. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Section - I
Q.1. Find the sum of the zeroes of the polynomial 2x2 – 8x + 6. (1 Mark)
Ans. Let p(x) = 2x2 – 8x + 6
∵ sum of zeroes = −coefficient of x / coefficient of x2
= -(-8) / 2 = 8 / 2 = 4.
Q.2. In an A.P., if d = – 4, n = 7, an = 4, then find the value of a. (1 Mark)
OR
How can 325 can be expressed as a product of its primes? (1 Mark)
Ans. In the given A.P., d = – 4, n = 7, an = 4
an = a + (n – 1) d
∴ 4 = a + (7 – 1) (– 4) = a – 24
∴ a = 4 + 24.
∴ a = 28.
OR
325 = 5 × 5 × 13
= 52 × 13.
Q.3. Find the distance between the points A (0, 6) and B(0, –2). (1 Mark)
Ans. The distance between two points (x1, y1) and (x2, y2) is given as :
Where, x1 = 0, y1 = 6 and x2 = 0, y2 = –2
So, distance between A (0, 6) and B (0, –2)

= √82
= 8
Q.4. If the distance between the points (4, p) and (1, 0) is 5, then find the value of p. (1 Mark)
Ans. By distance formula, distance between two points (x1, y1) and (x2, y2) is given by,
(x1, y1) = (4, p) and (x2, y2) = (1, 0)
∴ 


∴ 25 = 9 + p2
p2 = 16 or p = ±4.
Q.5. Evaluate  (1 Mark)
(1 Mark)
Ans.

Q.6. The tangent at any point of a circle is perpendicular to the .............. through the point of contact. (1 Mark)
OR
In ΔABC, DE || BC, find the value of x. (1 Mark) Ans. The tangent at any point of a circle is perpendicular to the 'RADIUS' through the point of contact.
Ans. The tangent at any point of a circle is perpendicular to the 'RADIUS' through the point of contact.
OR
As DE || BC
∴ AD / DB = AE / EC
or, x / x + 1 = x + 3 / x + 5
or, x2 + 5x = x2 + 4x + 3
or, x = 3
Q.7. Find the 11th term of the A.P. : (1 Mark)
(1 Mark)
OR
What is the sum of five positive integers divisible by 6.
Ans. In the given A.P., a = – 3 and d =
Thus, the 11th term is
t11 = -3 + (11 - 1) (5 / 2) = 22
OR
Here, a = 6, d = 6 and n = 5
∵ Sn = n / 2[2a + (n - 1)d]
S5 = 5 / 2 [2 x 6 + (5 - 1)(6)]
= 5 / 2 [ 12 + 4 x 6]
= 5 / 2 [12 + 24]
= 5 x 18 = 90.
Q.8. HCF × LCM = ..................... × (second number). (1 Mark)
Ans. HCF × LCM = product of two numbers = first number × second number.
Q.9. If the quadratic polynomial is ax2 + bx + c, then find product of zeroes. (1 Mark)
Ans. If the quadratic polynomial is ax2 + bx + c, then product of zeroes is, α × β = (c x a)
Q.10. In two triangles if the sides of one triangle are proportional to the sides of another triangle, then the two triangles are similar by .................. test of similarity and hence corresponding angles are equal. (1 Mark)
Ans. SSS (side-side-side) test of similarity.
Q.11. Find the median of the data, using an empirical relation when it is given that Mode = 12.4 and Mean = 10.5. (1 Mark)
Ans. Median =

= 12.4 / 3 + 21 / 3
= 33.4 / 3
= 11.13
Q.12. If two positive integers p and q can be expressed as p = ab2 and q = a3b; a, b being prime numbers, Find LCM of (p, q). (1 Mark)
OR
Find a quadratic polynomial, whose zeroes are –3 and 4. (1 Mark)
Ans. P = ab2 = a × b × b and q = a3b = a × a × a × b
Thus, LCM of p and q = a × a × a × b × b = a3b3.
OR
x2 – (α + β)x + αβ = 0
Here, roots of the quadratic polynomial are given as −3 and 4.
∴ Sum of the roots = −3 + 4 = 1
and Product of the roots = −3 × 4 = −12
∴ The quadratic polynomial is = x2 – (α + β)x + αβ
= x2 – x – 12
Q.13. If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then find the value of k. (1 Mark)
Ans. For parallel lines (or no solution)
a1 / a2 = b1 / b2 ≠ c1 / c2
∴ 3 / 2 = 2k / 5 ≠ -2 / 1
∴ 4k = 15 or k = 15 / 4.
Q.14. In Figure, DE || BC. Find the length of side AD, given that AE = 1.8 cm, BD = 7.2 cm and CE = 5.4 cm. (1 Mark) Ans. Given DE || BC
Ans. Given DE || BC
∴ AD / BD = AE / CE
⇒ AD / 7.2 = 1.8 / 5.4
∴ 
= 2.4 cm.
Q.15. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. What is the length of PQ? (1 Mark)
Ans. We know that the radius is perpendicular to tangent.
In ΔOPQ, we have ∠P = 90°
By Pythagoras Theorem,
OQ2 = PQ2 + OP2
(12)2 = PQ2 + (5)2
⇒ 144 = PQ2 + 25
⇒ PQ2 = 144 – 25 = 119
⇒ PQ = √119 cm.
Q.16. If area of quadrant of a circle is 38.5 cm2 then find its diameter (use π = 22 / 7) (1 Mark)
OR
What is the area of the largest square that can be inscribed in a circle of radius 12 cm? (1 Mark)
Ans. Area of quadrant = 1 / 4 x 22 / 7 x r2 = 38.5 (use π = 22 / 7)
⇒ r = 7 cm
∴ diameter = 14 cm
OR
Radius of the circle= 12 cm.
∴ Diameter of circle = 24 cm.
∴ Diagonal of square = 24 cm
Let the side of square = x cm.
x2 + x2 = (24)2
(By Pythagoras theorem) or, 2x2 = 24 × 24
or, 2x2 = 24 × 24
or,
Area of square = x2 = 288 cm2.
Section - II
Q.17. Following figure depicts a park where two opposite sides are parallel and left and right ends are semicircular in shape. It has a 7 m wide track for walking. Two friends Seema and Meena went to the park.
Q.18.

Q.19. To conduct sports day activities in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distances of 1 m form each other along AD, as shown in figure.

Q.20. Form a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and angle of elevation of the top of the flagstaff from P is 45°.

Part - B
All questions are compulsory. In case of internal choices, attempt anyone.
Q.21. Find the zeroes of the quadratic polynomial √3x2 – 8x + 4√3. (2 Mark)
Ans. Let p (x) = √3x2 – 8x + 4√3
∴ p (x) = 0
√3x2 – 6x – 2x + 4√3 = 0
√3x (x – 2√3 ) – 2(x – 2√3 ) = 0
( √3x – 2) (x – 2√3 ) = 0
x = 2 / √3 or 2√3
∴ Zeroes are 2 / √3 and 2√3.
Q.22. Find the value of k, for which the quadratic equation 4x2 + 4√3x + k = 0 has equal roots. (2 Mark)
Ans. An equation has equal roots if the discriminant b2 – 4ac = 0
In the given equation
4x2 + 4√3 x + k = 0, a = 4, b = 4√3 , c = k
∴ Discriminant = (4√3)2 – 4 (4)(k) = 0
48 – 16k = 0
16k = 48 or k = 3.
Q.23. Find how many integers between 200 and 500 are divisible by 8. (2 Mark)
Ans. Integers divisible by 8 are 208, 216, 224, ......, 496.
This is an A.P.
Given, a = 208, d = 8 and an = 496 (last term)
Let the numbers of terms in A.P. be n.
∵ an = a + (n – 1)d
∴ 208 + (n – 1) 8 = 496
(n – 1) 8 = 496 – 208
n – 1 = 288 ÷ 8
∴ n – 1 = 36
n = 36 + 1 or n = 37
Hence, required integers divisible by 8 = 37.
Q.24. Find the ratio in which the segment joining the points (1, – 3) and (4, 5) is divided by x-axis ? Also find the coordinates of this point on x-axis. (2 Mark)
Ans. Let the required point be P(a, 0) and required ratio AP : PB = k : 1
∴ a = 4K + 1 / K + 1
and 0 = 5K - 3 / K + 1
⇒ K = 3 / 5 or required ratio is 3 : 5
∴
Point P is (17 / 8, 0)
Q.25. Evaluate : (2 Mark)
(2 Mark)
OR
If two coins are tossed simultaneously. Find the probability of getting 2 heads. (2 Mark)
Ans.


= 1 + 3 + 2 – 1 = 5
OR
Two coins are tossed simultaneously.
Total outcomes = {HH, HT, TH, TT}
Favourable outcomes (exactly 2 heads) = {HH}
Probability = Favorable number of outcomes / Total number of outcomes
= 1 / 4
Q.26. Find the mode of the following frequency distribution (2 Mark)
OR
Prove that the tangents drawn at the ends of a diameter of a circle are parallel. (2 Mark)
Ans.
Here, modal-class = 35 – 40
Now, l = 35, f1 = 50, f0 = 34, f2 = 42, h = 5
Mode = 




OR ∠OLA = 90°
∠OLA = 90°
∠OMD = 90°
∠OLA= ∠OMD
OLA and OMD are alternate pair of angles for the lines AB, CD and transversal LM.
∴ Tangent AB || Tangent CD.
All questions are compulsory. In case of internal choices, attempt anyone.
Q.27. 144 cartons of Coke cans and 90 cartons of Pepsi cans are to be stacked in a canteen. If each stack is of the same height and if it contain equal cartons of the same drink, what would be the greatest number of cartons each stack would have? (3 Mark)
Ans. Since, the greatest number of cartons is the HCF of 144 and 90
144 = 24 × 32
90 = 2 × 32 × 5
Therefore, HCF = 2 × 32 = 18
Thus the greatest number of cartons = 18.
Q.28. Determine an A.P. whose third term is 9 and when fifth term is subtracted from 8th term, we get 6. (3 Mark)
OR
Find two consecutive positive integers sum of whose squares is 365. (3 Mark)
Ans. Let the first term be a and the common difference be d.
Given, a3 = 9 or, a + 2d = 9 ....(i)
and a8 – a5 = 6
or, (a + 7d) – (a + 4d) = 6
or, 3d = 6
or, d = 2 ....(ii)
Substituting the value of d in equation (i), we get
or, a + 2(2) = 9
or, a = 5
So, A.P. is 5, 7, 9, 11, .....
OR
Let two consecutive positive integers be x and x + 1.
∴ x2 + (x + 1)2 = 365
⇒ x2 + x – 182 = 0
(x + 14)(x – 13) = 0
∴ x = 13
Hence, two consecutive positive integers are 13 and 14.
Q.29. Find the point on y-axis which is equidistant from the points (5, –2) and (–3, 2). (3 Mark)
Ans. Let the required point on y-axis be (0, b)
∴ (5 – 0)2 + (–2 – b)2 = (–3 – 0)2 + (2 – b)2
⇒ 29 + 4b + b2 = 13 + b2 – 4b
⇒ b = – 2
∴ Required point is (0, –2)
Q.30. In given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. Find the length of TP. (3 Mark) OR
OR
In the figure given below, ∠BAC = 90 and AD ⊥ BC, then prove that : BD × CD = AD2 (3 Mark) Ans. Join OT and OQ.
Ans. Join OT and OQ.
TP = TQ
∴ TM ⊥ PQ and bisects PQ
Hence, PM = 4 cm
Therefore, OM =
 Let TM = x
Let TM = x
From ΔPMT,
PT2 = x2 + 16
From ΔPOT,
PT2 = (x + 3)2 – 25
Hence
x2 + 16 = x2 + 9 + 6x – 25
⇒ 6x = 32 ⇒ x = 16 / 3
Hence
∴ PT = 20 / 3 cm
OR
In ΔABD and ΔCAD,
∠ADB = ∠ADC = 90°
Suppose ∠ABD = θ then
∠BAD = 90° – θ
But ∠A = 90°,
∴ ∠CAD = θ
Thus ∠ABD = ∠CAD
By AA similarity, we get
ΔABD ∼ ΔCAD
⇒ AD / BD = CD / AD
i.e., BD × CD = AD2
Hence Proved
Q.31. If 4 tan θ = 3, evaluate (3 Mark)
(3 Mark)
Ans.  Given, 4 tan θ = 3
Given, 4 tan θ = 3
⇒ tan θ = 3 / 4
∴ In right triangle ABC,
tan θ = 3 / 4 = AB / BC
⇒ AB = 3x, BC = 4x
[Using Pythagoras theorem]
= √25x2 = 5x
∴ sin θ = AB / AC = 3x / 5x = 3 / 5
cos θ = BC / AC = 4x / 5x = 4 / 5

= 13 / 11
Q.32. Find the mode of the following frequency distribution. (3 Mark)
Ans.
Modal-class =30 – 40
⇒ l = 30, f0 = 10, f1 = 16, f2 = 12, h = 10
Mode =



= 30+6
= 36.
Q.33. A box consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Ramesh, a shopkeeper will buy only those shirts which are good but ‘Kewal’ another shopkeeper will not buy shirts with major defects. A shirt is taken out of the box at random. What is the probability that: (3 Mark)
(i) Ramesh will buy the selected shirt ?
(ii) ‘Kewal ‘ will buy the selected shirt ?
Ans. (i) Number of good shirts = 88
P (Ramesh buys good shirts) = 88 / 100 or 22 / 25
(ii) Number of shirts without major defect = 96
P (Kewal buys defected shirts) = 96 / 100 or 24 / 25
All questions are compulsory. In case of internal choices, attempt anyone.
Q.34. Find the value of a, b and c such that the numbers a, 7, b, 23 and c are in A.P. (5 Mark)
Ans. Since, a, 7, b, 23 and c are in A.P.
Let the common difference be d
∴ a + d = 7 .....(i)
and a + 3d = 23 .....(ii)
From (i) and (ii), we get
a = – 1 and d = 8
Again, b = a + 2d
b = – 1 + 2 × 8
or, b = – 1 + 16
or, b = 15
∴ c = a + 4d
= – 1 + 4 × 8
= – 1 + 32
c = 31
∴ a = – 1, b = 15 and c = 31.
Q.35. Find the coordinates of the point which divide the line segment joining A(4, – 3) and B(– 4, – 6) into three equal parts. (5 Mark)
Ans. Let P(x1, y1) and Q(x2, y2) are two points which divide AB in three equal parts.
P divides AB in the ratio of 1 : 2 and Q divides AB in the ratio 2 : 1.
By section formula
P(x1, y1) =


Q(x2, y2) = 


Q.36. Draw two concentric circles of radii 2 cm and 5 cm. Take a point P on the outer circle and construct a pair of tangents PA and PB to the smaller circle. Measure PA. (5 Mark)
OR
A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of wire. (5 Mark)
Ans. Steps of construction
1. Draw a circle with radius 2 cm and centre at O.
2. Draw another circle with radius 5 cm and same centre O.
3. Take a point P on the circumference of outer circle and join O to P.
4. Taking OP as diameter draw another circle which intersects the smallest circle at A and B.
5. Join A to P and B to P
Hence, PA and PB are the required tangent.
Measure of PA = 
OR
According to question,
⇒ r2 = 1 / 900
⇒ r = 1 / 30
⇒ Thickness of wire = 1 / 15 cm.
|
303 docs|7 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Basic) - 2 - CBSE Sample Papers For Class 10
| 1. What is the importance of solving sample question papers for the CBSE Class 10 Mathematics exam? |  |
| 2. How can solving sample question papers help in improving exam performance? |  |
| 3. Are the CBSE sample question papers representative of the actual exam difficulty level? |  |
| 4. Can solving sample question papers alone guarantee success in the CBSE Class 10 Mathematics exam? |  |
| 5. How should one approach solving sample question papers effectively for the CBSE Class 10 Mathematics exam? |  |

|
Explore Courses for Class 10 exam
|

|