Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 2 | CBSE Sample Papers For Class 10 PDF Download
Class X
Mathematics – Standard (041)
Sample Question Paper 2019-20
Max. Marks: 80
Duration : 3 hrs
General Instructions:
(i) All the questions are compulsory.
(ii) The question paper consists of 40 questions divided into 4 sections A, B, C, and D.
(iii) Section A comprises of 20 questions of 1 mark each. Section B comprises of 6 questions of 2 marks each. Section C comprises of 8 questions of 3 marks each. Section D comprises of 6 questions of 4 marks each.
(iv) There is no overall choice. However, an internal choice has been provided in two questions of 1 mark each, two questions of 2 marks each, three questions of 3 marks each, and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
(v) Use of calculators is not permitted.
Section A
Q 1. If two solid hemispheres of the same base radius r are joined together along their bases, then volume of this new solid is (1 Mark)
(a) 4/3πr3
(b) 1/3πr3
(c) 2/3πr3
(d) 4πr2
Ans: (a)
When two solid hemispheres of the same base radius r are joined together along their bases, then new solid formed is a sphere of radius r.
∴ Volume of this new solid formed 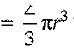
Q 2. If α and β and are zeroes of polynomials p (x) = x2 + x + 1, then the values of α + β is (1 Mark)
(a) -1
(b) -2
(c)-6
(d) -4
Ans: (a)
Since, α and β are zeroes of p( x) = x2 + x + 1
Q 3. If 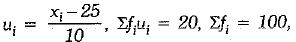 then
then 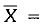 (1 Mark)
(1 Mark)
(a) 23
(b) 24
(c) 27
(d ) 25
Ans: (c)
Q 4. If sin A = 1/2 then the value of cot A is : (1 Mark)
(a) √3
(b) 1/ √3
(c) √3/2
(d) 1
Ans: (a)
Given, sin A = 1/2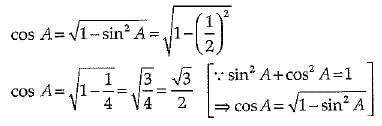
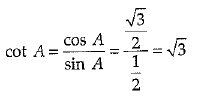
Q 5. In an isosceles ΔABC right angled at C with AC =4 cm, length of AB = ? (1 Mark)
(a) 32 cm
(b) 16 cm
(c) 4√2 cm
(d) 16√2 cm
Ans: (c)
Given, AC = 4 cm and ABC is an isosceles triangle right angled at C.
CB = AC = 4 cm
By Pythagoras Theorem in right triangle, right angled at C,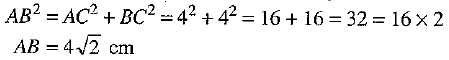
Q 6. The distance between the points 0(0,0) and P( 3,4) is (1 Mark)
(a) 6 units
(b) 5 units
(c) 4 units
(d) 2 units
Ans: (b)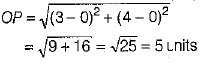
Q 7. Given that sin α = 1/2 and cos β = 1/2 then the value of (α + β) is (1 Mark)
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Ans: (d)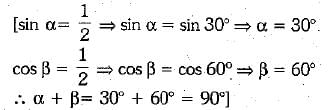
Q 8. The quadratic equation 2x2 - √5x + 1 = 0 has (1 Mark)
(a) two distinct real roots
(b) two equal real roots
(c) no real roots
(d) more than 2 real roots
Ans: (c)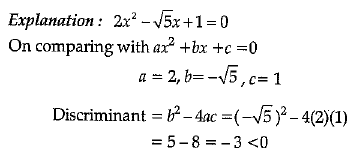
Therefore, the equation has no real roots
Q 9. The curved surface area of hemisphere of radius 7 cm is _________________ . (1 Mark)
Ans: 308 cm2
Radius of hemisphere, r = 7 cm
∴ Curved surface area of the hemisphere = 
Q 10. If 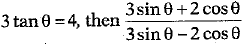 is equal to (1 Mark)
is equal to (1 Mark)
(a) 3
(b) 4
(c) 2
(d) 5
Ans: (a)
[∴ dividing numerator and denominator by cos θ ]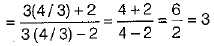
Q 11. The total surface area of the given solid is _______. (1 Mark)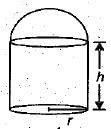
Ans: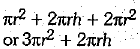
Q 12. Find a quadratic polynomial, whose zeroes are -3 and 4. (1 Mark)
Ans: x2 - (α + β) + αβ
Here, roots of the quadratic Polynomial are given as - 3 and 4.
∴ Sum of the roots = - 3 + 4 = 1
and Product of the roots = - 3 X 4 = - 1 2
∴ The quadratic polynomial is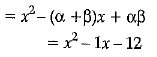
Hence the required polynomial is 
Q 13. The following questions consist of two statements - Assertion (A) and Reason (R). Answer these questions selecting the appropriate option given below : (1 Mark)
(a) Both A and R are true and R is the correct explanation for A.
(b) Both A and R are true and R is not the correct explanation for A.
(c) A is true but R is false.
(d) A is false but R is true.
Assertion (A) : The arithmetic mean of the following given frequency distribution table is 9.
Reason (R): 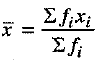
Ans: (a)
Q 14. The sum of all natural numbers from 1 to 100 is ______. (1 Mark)
Ans: We know that natural numbers forms an AP with first term a=1 and condition difference d=1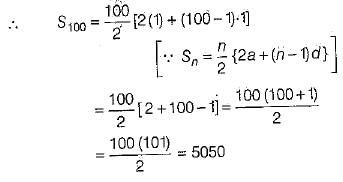
Q 15. If a number x is chosen from the numbers 1, 2, 3 and a number y is selected from the numbers 1, 4, 9, then P(xy < 9) =_______. (1 Mark)
Ans: 5/9
[Sample space = 3 x 3 = 9 and xy < 9
are (1, 1), (1, 4), (2, 1), (2, 4), (3, 1) i.e., 5 cases
Hence 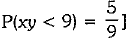
Q 16. Find the value of 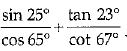 (1 Mark)
(1 Mark)
Ans: 2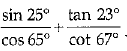
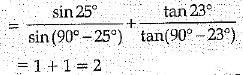
Q 17. if sin A = 3/4, calculate sec A. (1 Mark)
Ans: 4/√7
Given sin A = 3/4
we know that
sin2 A + cos2 A = 1
cos2 A = 1 - sin2 A
Q 18. What is the 15th term of the sequence defined by 
or
How many terms are there in the following AP?
25, 25, 30, .....100 (1 Mark)
Ans: 17
we have 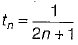
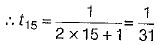 [∵ putting n = 15, given]
[∵ putting n = 15, given]
or
Let the number of terms be n.
We have, an = 100, a = 20, d = 5
∴ Using the formufa, an = a + (n -1 )d
= 10 = 20+ (n-1) (5)
n - 1 = 16
n = 17
Q 19. Find the Common difference, if 17th term of an A P exceeds its 10th term by 14 (1 Mark)
Ans: 14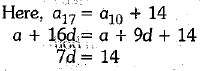
Q 20. In ΔABC, DE ║ BC, find the value of x (1 Mark)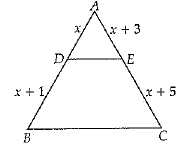
OR
In the given figure, PQ and PR are tangents to the circle with centre O such that ∠QPR = 50°, then find ∠OQR.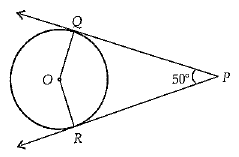
Ans: x= 3 or ∠OQR = 250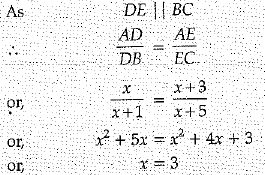
or
Section B
Q 21. Write the smallest number which is divisible by both 306 and 657. (2 Mark)
Ans: 22338
The smallest number divisible by 306 and 657 is their LCM.
we have
306 = 2 x 153 = 2 x 3 x 51 = 2 x 3 x 3 x 17 = 2 x 32 x 17
and 657 = 3 x 219 = 3 x 3 x 73 = 32 x 73
∴ LCM = 21 x 32 x 171 x 731 = 2 x 9 x 17 x 73 = 22338
Q 22. The sum of two numbers is 9 and the sum of their reciprocals is 1/2. Find the numbers. (2 Mark)
Ans: 3 and 6
Let one number be x, then the other number will be (9-x)
According to the question
sum of reciprocals = 1/2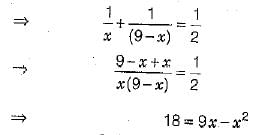
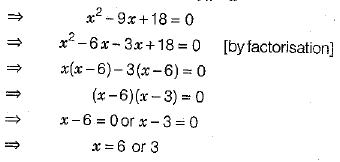
Q 23. In the figure, ABC is a triangle in which AD ⊥ BC, show that (2 Mark)
ACS = AB2+BC2-2BC.BD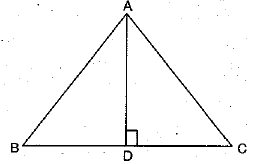
OR
In the given figure, ABC and DBC are two triangles o n the sam e base B C . If AD intersects BC at O, show that:
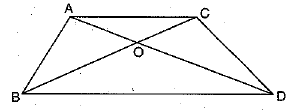
Ans:
In ΔABC, AD⊥ BC
Now, in ΔADC, ∠D = 90°
∴ AC2 = AD2 + DC2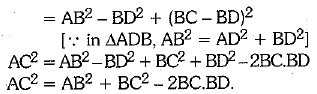
or
Draw AP⊥ BC and DM ⊥ BC. In AAOP and ΔDOM, we hav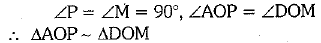
[by AA similarity criterion]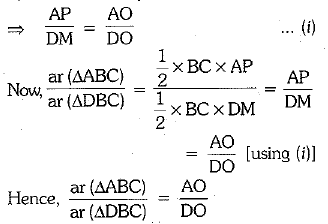
Q 24. Prove that the point (3/ 0), (6, 4) and (-1,3) are the vertices of a right angled isosceles triangle. (2 Mark)
Ans:
Let A(3,0), B(6,4) and C(-l, 3)
AB2 = CA2 or, AB = CA
∴ Triangle is isosceles.
25 + 25 = 50
Also, AB2 + CA2 = BC2
Since, Pythagoras theorem is verified, therefore triangle is a right angled triangle.
Q 25. The larger of two supplementary angles exceeds the smaller by 18°. Find the angles. (2 Mark)
Ans: 99° and 81° or Sumit is 450
The larger of two supplementary angles be x.
∴ Other angle = (180° - x)
According to given condition, we have
x - (180° - x ) = 18°
⇒ x - 180° + x - 18°
⇒ 2x = 198°
⇒ x = 99°
∴ 180° - x = 180° - 9 9 ° = 81°
Hence, the angles are 99° and 81°.
Or
Sumit is 3 times as old as his son. Five years later, he shall be two and a half times as old as his son. How old is Sumit at present ?
Solution: Let the present age of Sumit be x years and the present age of his son be y years.
Using the given information, we have
x = 3y ...(1)
Five years later, Sumit's age = (x + 5) years and his son’s age = (y + 5) years
Using the given information, we have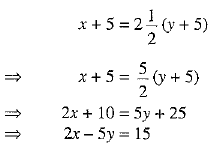 ...(2)
...(2)
Putting the value of x from (1) in (2), we get
2 x 3y - 5y = 15 ⇒ y — 15
From (1), we have
x — 3y — 3 x 15 — 45
Hence, the present age of father , sumit is 45 years.
Q 26. Compute the Arithmetic Mean for the following data (2 Mark)

Ans: 28.6
Here, h = 10
Let assumed mean (A) = 3
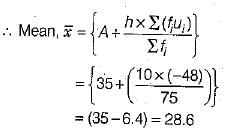
Section C
Q 27. Prove that 2 + 5 √3 is an irrational number, given that √3 is an irrational number. (3 Mark)
Ans:
Suppose, 2 + 5 √3 is a rational number. Then there exists co-prime integers a and b such that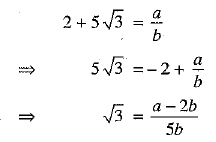
⇒ √3 is a rational number. [∵ a and b are integers so that 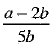 is a rational number]
is a rational number]
This contradicts the given fact that √3 is an irrational number. So, our supposition is wrong.
Hence, 2 + 5 √3 is a irrational number
Or
Using Euclid’s Algorithm, find the HCF of 2048 and 960.
Ans:
Given integers are 2048 and 960.
Clearly 2048 > 960.
Applying Euclid’s division algorithm, we get
2048 = 960 x 2 + 128
960 = 128 x 7 + 64
128 = 64 x 2 + 0
In the last equation, the remainder is zero and divisor in the last equation is 64.
Hence, HCF of 2048 and 960 = 64.
Q 28. Read the following passage and answer the questions that follows : Quotient and remainder on dividing x3 - 3x2 + x + 2 by a polynomial g(x) are (x - 2) and - 2x + 4 , respectively. Ahmed was asked to find the g(x) . He was little puzzled and was thinking how to proceed. His classmate Vxdya helped him by suggesting that he should use the Euclid's division algorithm to find the value of g(x). Find g (x). (3 Mark)
Ans:
Let p(x) - x3- 3x2+ x +2,
q(x) = x - 2 and
r(x ) = - 2x + 4
By using division algorithm,
we have Dividends (Divisor x Quotient) + Remainder
⇒ p(x) = g(x) x q(x) + r(x)
On putting the values of p(x), q(x) and r(x), we get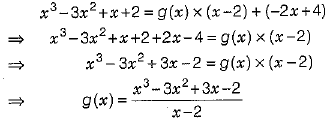
Now, using long division method, divide
x3- 3x2+ 3x - 2 by x - 2 , we get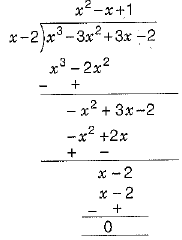
Thus, we get quotient = x2 - x +1
Hence, g (x ) = x2- x + 1
Q 29 . A motor boat whose speed in still water is 5 km/h, takes 1 hour more to go 12 km upstream than to return downstream to the same spot Find the speed of the stream.
Or
A shopkeeper buys some books for Rs. 80. If he had bought 4 more books for the same amount, each book would have cost Rs. 1 less. Find the number of boobs he bought. (3 Mark)
Ans: Let the speed of the stream of water be x km/h
Effective speed of the boat during downstream = (5 + x) km/h
Effective speed of the boat during upstream = (5 - x) km/h
Distance covered — 12 km
According to the statement of the question, we have
⇒ 24x =25x2
⇒ x2 + 24x - 25 =0
⇒ (x+ 25) (x-1) = 0
x = -25, x = 1
Since the speed of the stream cannot be negative, therefore, negative value is not admissible
Thus, x = 1
Hence, the speed of thehstream of water is 1 km/h.
Or
Let the number of books bought be x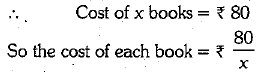
Now, when number of books bought is x + 4
then, cost of each book = 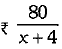
According to statement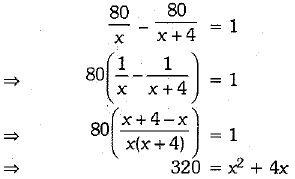
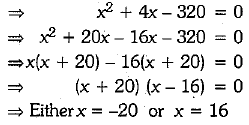
⇒ x = 16 [ ∵ x cannot be negative]
Hence, the number of books bought by the shopkeeper is 16.
Q 30. Show that : cosec2θ - tan2 (90° -θ) = sin2 θ + sin2 (90° - θ) (3 Mark)
Ans:
. LHS - cosec2 θ - tan2 (90° - θ)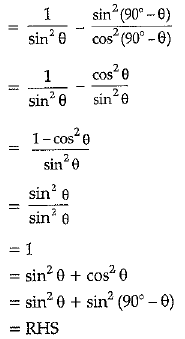
Q 31. In figure, a square OABC is inscribed in a quadrant OPBQ. If OA =15 cm, find the area of the shaded region. [Use π= 3.14] (3 Mark)
Ans:
Here OABC is a square inscribed in a quadrant OPBQ.
As all sides of a square are equal.
OA = AB = BC = CO = 15 cm
By Pythagoras theorem in ΔOAB,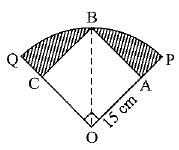
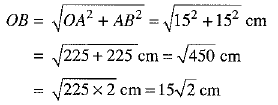
∴ Radius of the quadrant = OB = 15 √2 cm
Area of the shaded region - Area of a quadrant of a circle of radius OB (15√2 cm) - Area of a square of side OA = 15 cm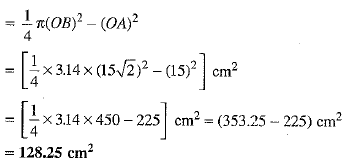
or
In figure, ABCD is a square with side 2 √2 cm and inscribed in a circle. Find the area o f the shaded region. [Use π= 3.14] (3 Mark)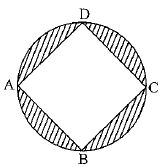
Ans:
Given that ABCD is a square with side 2√2 cm and inscribed in a circle. Join AC or BD. From right triangle ABC right angled at B, diagonal AC is given by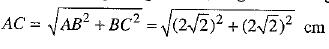
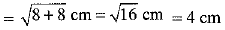
Also, BD = AC = 4 cm [Since diagonals of a square are equal]
Since the square is inscribed in a circle, therefore, the diagonal of the square is diameter of the circle.
Diameter of the circle = 4 cm
Radius of the circle = 2 cm
From the figure, Area of the shaded region = Area of the circle of radius 2 cm - Area of a square of side AB — 2√2 cm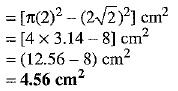
Q. 32 Prove that (3 Mark)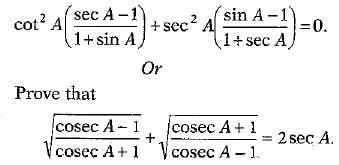
Ans: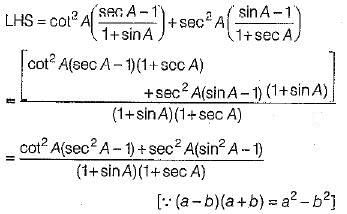



Q 33. Three horses are tethered with 7 m long ropes at the three comers of a triangular field having sides 20 m, 34 m and 42 m.
Find the area of the plot which can be grazed by the horses. Also, find the area of the plot which remains ungrazed. (3 Mark)
Ans: Here, radius of each Sector at A, B and c = 7m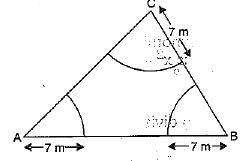
Now, area which can be grazed by three horses = Area of sectors with central angles
∠A, ∠B and ∠C, radius 7 m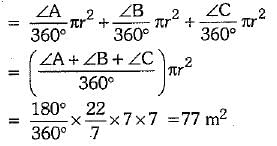
Area of the plot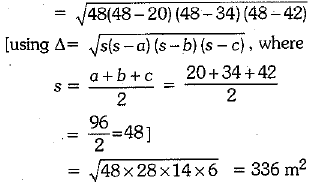
∴ Area of the plot which remains ungrazed = 336 - 77 = 259 m2
Q 34. Find the HCF of 180,252 and 324 by Euclid's Division algorithm. (3 Mark)
Ans:
since
324 = 252 x 1 + 72
252 = 72 x 3 + 36
72 = 36 x 2 + 0
∴ HCF(324,252) - 36
180 =36 x 5 + 0
∴ HCF(36f 180) =36
∴ HCF of 180,252 and 324 is 36.
Section D
Q 35. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio. (4 Mark)
Ans:
Given : A triangle ABC in which a line parallel to BC intersects other two sides AB and AC at D and E respectively.
To prove : 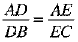
Construction : Join BE, CD and draw DM L AC and EN A. AB.
Proof : Since EN is perpendicular to AB, therefore, EN is the height of triangles ADE and BDE.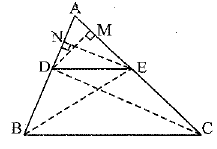
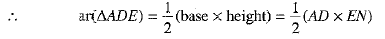 ..(1)
..(1)
and ....(2)
....(2)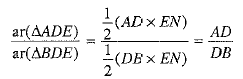 ..(3) using 1 and 2
..(3) using 1 and 2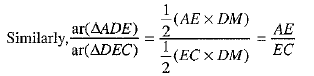 ...(4)
...(4)
Note that ABDE and ADEC are on thesame base DE and between the same parallel BC and DE
∴ ar(ΔBDE) = ar(ΔDEC) ..(5)
From (4) and (5), we have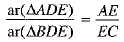 ..(6)
..(6)
Again from (3) and (6), we have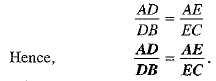
Q 36. Find the common difference of an AP whose first term is 1 and the sum of the first four terms is one-third to the sum of the next four terms. (4 Mark)
Ans: Let a be the first term and d be the common difference of an AP
Given, a = 1 and sum of first four terms = 1/3( sum of next four term)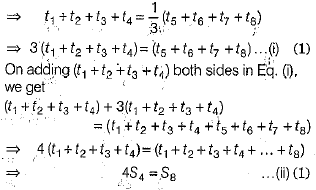
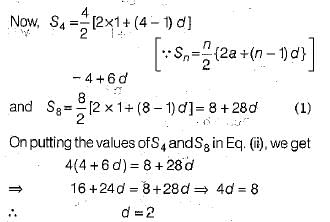
Hence, the required common difference is 2
Q. 37. A and B working together can do a piece of work in 6 days. If A takes 5 days less than B to finish the work, in how many days B alone can do the work ? (4 Mark)
OR
Solve for x :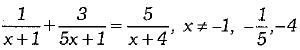
Ans: Let B takes x days to finish the work and A takes (x - 5) days to finish the same work.
A’s one day work + B’s one day work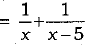

12x - 30 - x2 - 5x
⇒ x2 - 5x - 12x + 30 - 0
⇒ x2 - 17x + 30 = 0
⇒ x2 - 15x - 2x + 30 — 0
⇒ x(x- 15) -2(x- 15) = 0
⇒ (x - 1 5) (x - 2 ) = 0
x = 15 or x = 2
But x cannot be less than 6. So, B alone can finish the work in 15 days.
or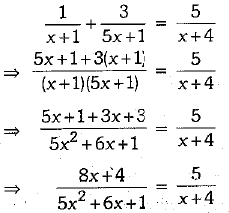
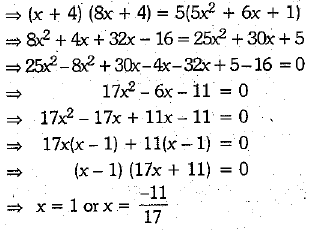
Q 38. The angle of depression of two ships from an aeroplane flying at the height of 7500 m are 30° and 45°. If both the ships are in the same line that one ship is exactly behind the other, find the side such distance between the ships. (4 Mark)
OR
The angle of elevation of the top Q of a vertical towerP Q from a point X on the ground is 60°. From a point y 40 m vertically above X, the angle of elevation of the top Q of tower is 45°. Find the height of the tower PQ and the distance PX. (Use √3= 1.73)
Ans: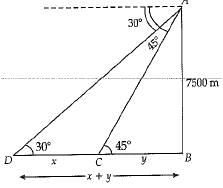
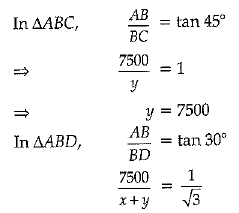
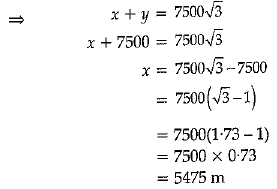
Hence, the distance between two ships = 5475 m
or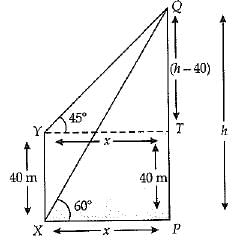
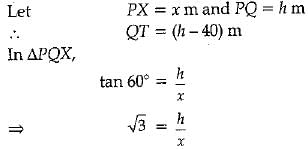
⇒ h = √3x .(1)
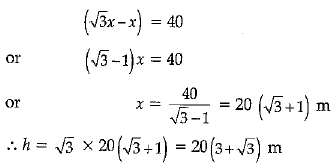
20(3 +1.73) = 20 X 4.73
Hence, the height of tower is 94.6 m.
Q 39. Which term o f the Arithmetic Progression - 7, - 12, - 1 7 . - 2 2 , . . . . will be - 82 ? Is - 100 any term of the A.P. ? Give reason for your answer. (4 Mark)
Ans: The given A.P. is - 7, - 12, - 17, - 22,....
First term , a = - 7. and common difference, d = - 12 - ( - 7 ) = - 12 + 7 = - 5
Let - 82 be its nth term.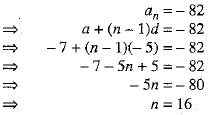
Hence, - 82 is the 16th term of the given A.P.
Let - 100 be its nth term.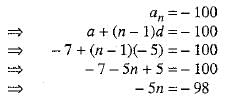
n=98/5 , which is a fraction.
Since number of terms cannot be in fraction.
Hence, - 100 is not any term of the given A.P.
or
How many terms of the Arithmetic Progression 45, 39, 33,.... must be taken so that their sum is 180 ? Explain the double answer.
Ans: The given A.P. is 45, 39, 33,.....
First term, a = 4 5 and common difference,
d = 39 - 45 = 6
Let 180 be the sum of its n terms.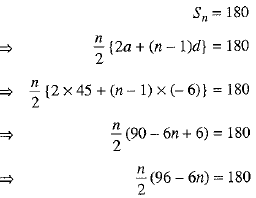
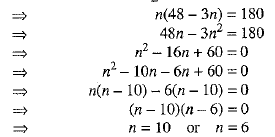
Sum of first 6 terms = Sum of first 10 terms = 180
Explanation of double answer
Here, common difference is negative.
7th term of the A.P. is given by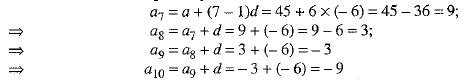
Sum of next 4 terms just after first 6 terms = a7 + a8 + a9 + a10 = 9 + 3 + (- 3) + (- 9) = 0.
Therefore, sum of first 6 terms is the same as the sum of first 10 terms.
Q 40. Find the median for the following data. (4 Mark)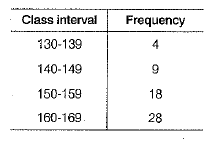

Ans: Here, given the frequency distributive table is not in continuous classes, so we convert it into continuous classes for finding, the median. For this, subtract 0,5 from lower limit of each class interval and add 0.5 to upper .limit of each class interval as shown in the table given below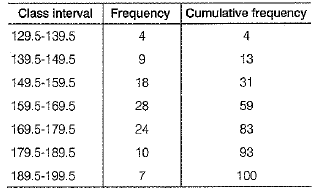
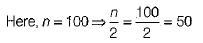
The cumulative frequency just greater than 50 is 59 and its corresponding class is 159.5-169.5.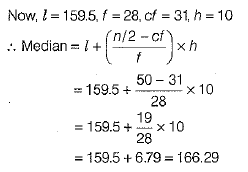
|
303 docs|7 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 2 - CBSE Sample Papers For Class 10
| 1. How can I access the CBSE Sample Question Paper for Class 10 Mathematics (2019-20)? |  |
| 2. Are the CBSE Sample Question Papers for Class 10 Mathematics (2019-20) helpful for exam preparation? |  |
| 3. Can I rely solely on the CBSE Sample Question Papers for Class 10 Mathematics (2019-20) to prepare for the board exam? |  |
| 4. How can I effectively use the CBSE Sample Question Papers for Class 10 Mathematics (2019-20) for practice? |  |
| 5. Are there any other resources available apart from the CBSE Sample Question Papers for Class 10 Mathematics (2019-20) to enhance my exam preparation? |  |

|
Explore Courses for Class 10 exam
|

|

















