Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 3 | Mathematics (Maths) Class 10 PDF Download
Class X
Mathematics – Standard (041)
Sample Question Paper 2019-20
Max. Marks: 80
Duration : 3 hrs
General Instructions:
(i) All the questions are compulsory.
(ii) The question paper consists of 40 questions divided into 4 sections A, B, C, and D.
(iii) Section A comprises of 20 questions of 1 mark each. Section B comprises of 6 questions of 2 marks each. Section C comprises of 8 questions of 3 marks each. Section D comprises of 6 questions of 4 marks each.
(iv) There is no overall choice. However, an internal choice has been provided in two questions of 1 mark each, two questions of 2 marks each, three questions of 3 marks each, and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
(v) Use of calculators is not permitted.
Section A
Q.1. A chord of circle of radius 14 cm subtends an angle of 45° at the centre. Then the area of the corresponding sector is (1 Mark)
(a) 50 cm2
(b) 11 cm2
(c) 100 cm2
(d) 80 cm2
Solution: Choice (b) is correct.
We have, Area Of the sector of Circle of radius 21 cm subtending an angle of 45° at the centre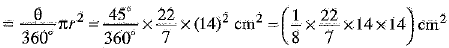
= (11 x 7 ) cm2 = 77 cm2
Q.2. The next term of the AP 5, 2, -1, -4,______ is (1 Mark)
(a) -3
(b) -7
(c) -5
(d) -6
Solution: b) Given, AP is 5,2, -1, - 4,__
Here, first term,a = 5
and common difference, d = 2 - 5 = -3
∴ Fifth term, T5 = a + (5-1)d = 5 + 4x(-3)
= 5 - 12 = -7
Q.3. Consider the following frequency distribution of the heights of 60 students of a class: (1 Mark)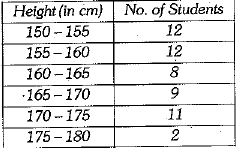
The sum of the lower limit of the modal class and the upper limit of the median class is:
(a) 315
(b) 320
(c) 325
(d) 300
Solution: (b) 320
[Here, Modal class is 155 - 160 and median class is 160 - 165
Now, required sum= 155 + 165 = 320
Q.4. The distance of the point P (- 6, 8) from the origin is : (1 Mark)
(a) 8
(b) 2√7
(c) 10
(d) 6
Solution: (c)
Explanation : Distance between two points (x1 y1) and (x2,y2) is given as,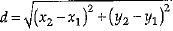
Where, x1 = -6, y1 = 8 and x2 = 0, y2 = 0
So, distance between P (-6,8) and origin 0 (0,0) is given by,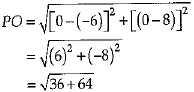
= √100
= 10
Q.5. Which of the following equations has 2 as a root ? (1 Mark)
(a) X2 - 4x + 5 = 0
(b) x2 + 3x - 12 = 0
(c) 2x2 - 7x + 6 = 0
(d) 3x2 - 6x - 2 = 0
Solution: Choice (c) is correct.
x2 - 4x + 5, (2)2 - 4(2) + 5 = 4 - 8 + 5 = 9 - 8=1 ≠ 0
x2 - 3x - 12, (2)2 - 3(2) - 12 = 4 - 6 - 12 = - 2 - 12 = - 14 ≠ 0
2x2 - 7x + 6, 2(2)2 - 7(2) + 6 = 8 - 14 + 6=14 - 14 = 0
3x2 - 6x - 2, 3(2)2 - 6(2) - 2 = 12 - 12 - 2 = -2 ≠ 0
∴ 2 is the root of the equation if 2x2 - 7x + 6 = 0
Q.6. The number of zeroes in a cubic polynomial may be atmost (1 Mark)
(a) 1
(b) 2
(c) 3
(d) 0
Solution: (c) A cubic poiynomial can have at most 3 zeroes.
Q.7. If sin α + sin2 α = 1, then the value of cos2 α + cos4 α is: (1 Mark)
(a) 0
(b) -1
(c) 1
(d) 2
Solution: (c) 1
[Given that sin α + sin2 α = 1
⇒ sin α = 1 - sin2 α ⇒ sin α = cos2 α
⇒ sin2 α = cos4 α ⇒ 1 - cos2 α = cos4 α
⇒ 1 = cos2 α + cos4 α]
Q. 8. If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then : (1 Mark)
(a) R1 + R2 = R
(b) R1+ R2 > R
(c) R1 + R2 < R
(d) Nothing definite can be said about the relation among R1 R2 and R
Solution: Correct option : (a) Explanation: According to question, Circumference of circle = Circumference of first circle + Circumference of second circle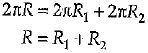
Q.9. The pair of linear equations 2ax + by = a, 6ax + 3by = 3a; a, b ≠ 0 is _________ .(consistent/inconsistent) (1 Mark)
Solution: consistent
Here, 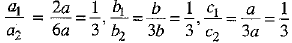
∴ 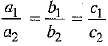
Hence, the given system of linear equation is consistent.
Q.10. If radius of circle is 8 cm and tangent is drawn from an external point to the circle is 15 cm, the distance from centre of circle to the external point is (1 Mark)
(a) 21 cm
(b) 16 cm
(c) 17 cm
(d) 18 cm
Solution: (c) Given, OG = 8 cm and PG = 15 cm.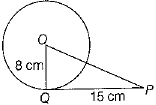
In right angled ΔOPQ, use Pythagoras theorm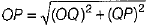
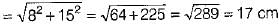
Q.11 . If R and r are the radii of top and bottom of the frustum, l is the slant height then curved surface area of the frustum of the cone = __________. (1 Mark)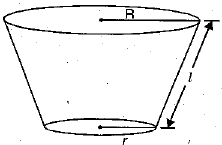
Solution: π (R + r) l sq. units.
Q.12. What is the frustum of a right circular cone of height 16 cm with radii of its circular ends as 8 cm and 20 cm has slant height equal to ? (1 Mark)
Solution: 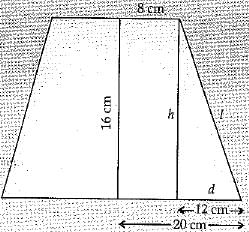
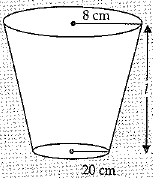
Slant height of the frustum
l = √h2 + d2 = √162 + (20 - 8)2
= √(16)2 + (12)2
= √256 + 144
= √400
= √20 cm
Q.13. The following questions consist of two statements - Assertion (A) and Reason (R). Answer these questions selecting the appropriate option given below : (1 Mark)
(a) Both A and R are true and R is the correct explanation for A.
(b) Both A and R are true and R is not the correct explanation for A.
(c) A is true but R is false.
(d) A is false but R is true.
Q. Assertion (A): The discriminant of the quadratic equation (x + 5)2 = 2(5x - 3) is - 124. Reason (R) : D = b2 - 4ac
Solution: Choice (a) is correct.
The given equation is
(x + 5)2 = 2(5x - 3)
⇒ x2 + 10x + 25 = 10x - 6
⇒ x2 + 0x +31 = 0
Comparing it with ax2 + bx + c = 0 we have
a = 1, b = 0, c = 31
∴ D = b2 - 4ac = (0)2 - 4(1)(31) = - 124
Q. 14. Statistics is the branch of mathematics which deals with _____ (1 Mark)
Solution: interpretation of data.
Q.15. The probability of selecting a red ball at random from a jar that contains only red, blue and orange ball is 1/4. The probability of selecting a blue ball at random from the same jar 1/3. If this jar contains 10 orange balls, then the total number of balls = _______. (1 Mark)
Solution: 24
[P (an orange ball = 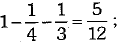
Number of orange ball = 10
∴ 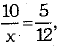 , where x is total number of ball
, where x is total number of ball
⇒ 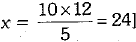
Q.16. Find the area of the triangle with vertices (0,0) (6,0) and (0,5) (1 Mark)
Solution: Area of triangle
= 1/2 [ x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
= 1/2 [0(0-5) + 6(5-0) + 0(0-0)]
= 1/2 [6 x 5] = 15 sq. units
Q.17. Find the perimeter of ΔABC. (1 Mark)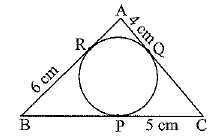
Solution: We know that the length of tangents drawn from an external point to a circle are equal.
CP = CQ, AR = AQ and BR = BP
Now perimeter of ΔABC = AB + BC + CA
= (AR + BR) + (BP + CP) + (AQ + CQ)
= (AR + AQ) + (BR + BP) + (CP + CQ)
= (AQ + AQ) + (BR + BR) + (CP + CP)
= 2AQ + 2BR + 2 CP
= 2(4) + 2(6) + 2(5) cm
= (8 + 12 + 10) cm
= 30 cm
Q.18. Find the length of the shadow on the ground of a pole of height 18m when the angle of elevation 9 of the sun is such that tan 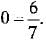 (1 Mark)
(1 Mark)
Solution: Let AB be the length of the shadow and height of the pole BC = 18 m and elevation ∠BAC = θ.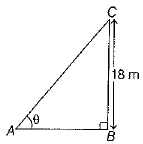
In right angled ΔABC,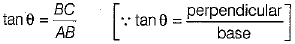

⇒ 6 x AB = 18 x 7 ⇒ AB = 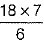 =21
=21
Hence, the length of the shadow is 21 m.
Q.19. How many terms of the AP 18,16,14,... be taken so that their sum is zero ? (1 Mark)
Solution: Here, given AP is 18, 16, 14,........
α = 18, d = -2 and Sn = 0
Now,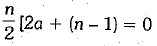
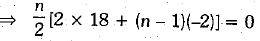
⇒ 18n - n2 + n =0
⇒ 19n - n2 = 0
⇒ n(19 - n) =0
⇒ n = 0 or n = 19
Q.20. For some integer q, every odd integer is of the form: (1 Mark)
(a) q
(b) q + 1
(c) 2q
(d) 2q + 1
Solution: Correct option: (d)
Explanation : According to Euclid's division lemma, a = bq + r, where o < r < b.
lf b = 2, then a — 2q or a — 2q + 1
Since a = 2q + 1 is not divisible by 2, then 2q + 1 is an odd integer.
Section B
Q.21. Points A(3,1), B(5,1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b. (2 Mark)
Solution: Given, points A(3, 1), B(5, 1), C(a, b) and D{4, 3) are the vertices of a parallelogram. The coordinates of the mid-point of diagonal AC are 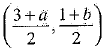
The coordinates of the mid-point of diagonal BD are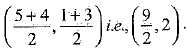
We know that the diagonals of a parallelogram bisect each other. So, coordinates of the mid-point of diagonal AC are the same as the coordinates of the mid-point of diagonal BD.
∴ 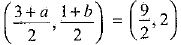
⇒ 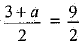 and
and 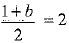
⇒ 3 + a = 9 and 1 + b = 4
⇒ a = 9 - 3 and b = 4 - 1
⇒ a = 6 and b = 3
Or
Points P and Q trisect the line segment joining the points A(- 2, 0) and B(0, 8) such that P is nearer to A. Find the coordinates Of points P and Q.
Solution: The given points are A(- 2, 0) and B(0, 8). P arid Q are the points of trisection such that P is nearer to A. Then AP - PQ = QB.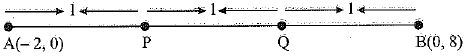
Therefore, point P divides AB internally in the ratio 1 : 2,
Using section formula, the coordinates of point P are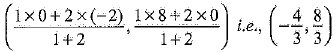
Also, point Q divides AB internally in the ratio 2:1,
Using section formula, the coordinates of point Q are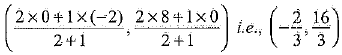
Hence, the points of trisection are P 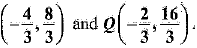
Q.22. In the given figure, if DE ║ BC, then find the value of x. (2 Mark)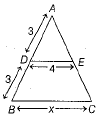
Solution: Given, DE║BC
⇒ 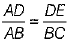 ...... (1)
...... (1)
[by basic proportionality theorem]
⇒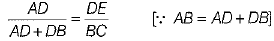
⇒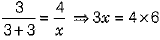
∴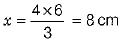 .....(1)
.....(1)
Q.23. Triangle ABC is right-angled at B and D is the mid-point of BC. (2 Mark)
Prove that: AC2 = 4AD2 - 3AB2
or
In a ΔPQR, N is a point on PR such that QN ⊥ PR. If PN.NR = QN2, prove that ∠PQR = 90°
Solution: Here, D is the mid-point of BC
⇒ BC = 2BD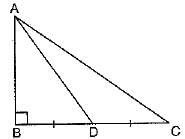
Now, in right AABD, we have
AD2 - AB2 + BD2 ...(i)
BD2 = AD2 - AB2 ...(ii)
In right AABC, we have
AC2 = 4BD2 + AB2 [using (i)]
= 4(AD2 - AB2) + AB2 [using (ii)
= 4AD2 - 4AB2 + AB2
= 4AD2 - 3AB2
Or
Here, QN ⊥ PR
⇒ ∠l = ∠2 — 90°
Also, PN.NR = QN.QN
⇒ 
∴ ΔPNQ - ΔQNR
⇒ ∠3 = ∠4 and ∠5 = ∠6
[∵ corresponding angles of similar Δs]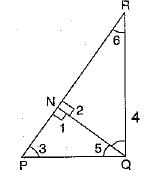
Now, in APQR, we have
∠3 + ∠4 + ∠5 + ∠6 = 180°
∠4 + ∠4 + ∠5 + ∠5 = 180°
[∵ ∠3 = ∠4 and ∠6 = ∠5]
⇒ 2(∠4 + ∠5) = 180°
⇒ ∠4 + ∠5 = 90°
⇒∠PQR = 90°
Q.24. In the given figure PQ is chord of length 6 cm of the circle of radius 6 cm. TP and TQ are tangents to the circle at points P and Q respectively. Find ∠PTQ. (2 Mark)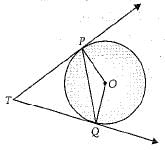
Solution: Here, PQ = 6 cm, OP = OQ = 6 cm
∴ PQ = OP = OQ
∴ ∠POQ = 60°
(angle of equilateral Δ.) 1/2
∠P = ∠Q = 90°
(radius ⊥ tangent)
∴ ∠PTQ + 90° + 90° + 60° = 360°
(angle sum property) 1/2
∠PTQ = 120°
Q.25. By using quadratic formula, show that the equation x2 - 8x + 18 = 0 has no solution. (2 Mark)
Solution: The given equation is
x2 - 8x + 18 = 0
Comparing it with ax2 + bx + c = 0, we have
a - 1, b = -8, c = 18
D = b2 -4ac
= (- 8)2 - 4(1)(18)
=64 - 72
= - 8 < 0
Here, D < 0.
∴ The given equation has no real roots.
Thus, the given equation has no real solution.
Q.26. The Arithmetic Mean of the following frequency distribution is 50. Find the value of p. (2 Mark)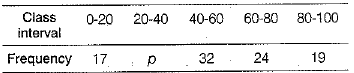
Or
The following distributive gives the statewise teacher ratio in higher secondary schools of India. Find the mode of the data.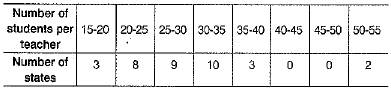
Solution: 
∴ Mean, 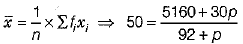
⇒ 4600 + 50p = 5160 + 30p
⇒ 50p - 30p = 5160 - 4600 ⇒ 20p = 560
∴ p = 28....(i)
Or
Here, the ciass 30-35 has maximum frequency. So, it is the modal class
∴ l = 30, h = 5, f1 = 10, f0 = 9 and f2 = 3
Mode = 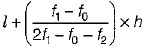 .......(1)
.......(1)
= 
= 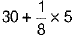
= 30 + 0.625 = 30.625.........(i)
Section C
Q.27. The perpendicular from A on side BC of a ΔABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2. (3 Mark)
Solution: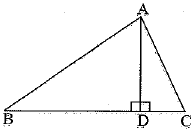
We have,
DB = 3 CD
∵ BC = BD + DC
⇒ BC = 3CD + CD
⇒ BC = 4CD
⇒ 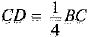
∴ 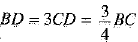
In right triangle ABD, right angled at D, we have
AB2 = AD2 + BD2
Also, in a right triangle ACD, right angled at D), we have
AC2 - AD2 + CD2
Subtracting (2) from (1), we get
AB2 - AC2 = BD2 - CD2
⇒ 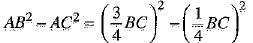
⇒ 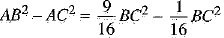
⇒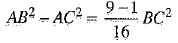
⇒ 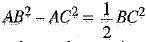
⇒ 2(AB2 - AC2) = BC2
⇒ 2AB2 = 2AC2) + BC2
Or
AD and PM are medians of triangles ABC and PQR respectively where ΔABC ~ ΔPQR. Prove that 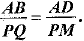
Solution: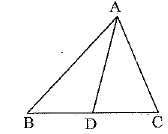
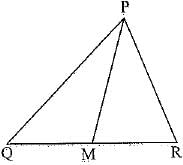
Given : Two triangles ABC and FOR such that ΔABC ~ ΔPQR and AD and P M are their medians.
To prove: 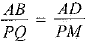
Proof: AD and PM are medians so that D and M are the mid-points of BC and QR respectively.
∴ BC = 2BD and QR = 2QM
Now, ΔABC ~ ΔPQR
∴ 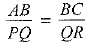 and ∠B = ∠Q
and ∠B = ∠Q
⇒ 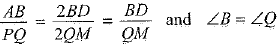
Thus, in ΔADB and ΔPMQ, we have
By SAS-criterion of similarity, we have
⇒ 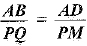
Q.28. Find the roots of the following equation (3 Mark)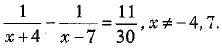
Or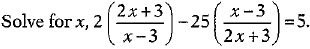
Solution: Given, equation is 
⇒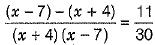
⇒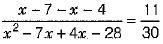
⇒ 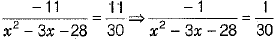
⇒ - 30 = x2 - 3x - 28 ⇒ x2 — 3x + 2 = 0 (1)
On comparing the standard quadratic equation ax2 + bx +c = 0, we get
a = 1, p = - 3 and c = 2
By using quadratic formula, we get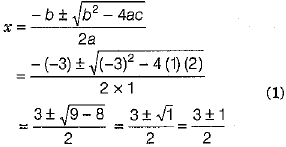
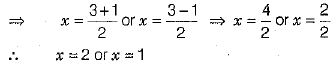
Hence, the roots of the given equation are 2 and 1. ......(1)
or
Let 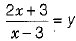 .....(i)
.....(i)
Then, 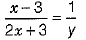 (1/2)
(1/2)
Therefore, the given equation reduces to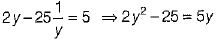
⇒ 2y2 - 5y -25 = 0 ⇒ 2y2 -10y + 5y - 25 = 0
[by factorisation method]
⇒ 2y (y -5 ) + 5(y-5) = 0 ⇒ (y-5)(2y + 5) = 0
⇒ 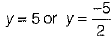 ......(i)
......(i)
Now, putting y = 5 in Eq. (i), we get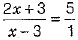
⇒ 5x - 15 = 2x + 3
⇒ 3x = 18 ⇒ x = 6.....(1/2)
Again, putting y = 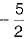 in Eq. (i), we get
in Eq. (i), we get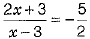
⇒ - 5x +15 = 4x + 6
∴ 9 x = 9 ⇒ x = 1
Hence, the values of x are 1 and 6.....(i)
Q.29. A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours it can go 40 km upstream and 55 km downstream. Determine the speed of the boat in still water. (3 Mark)
Or
At present Asha's age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age. Asha’s age would be one year less than 10 times the present ag e o f Nisha. Find the present ages of both Asha and Nisha.
Solution: Let the speed of boat in still water be x km/h and speed of the stream be y km/h. Effective speed in upward journey
= (x - y) km/h
Effective speed in downward journey
= (x + y) km/h
According to the statement of the question, we obtain
and 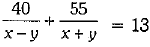
Put 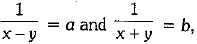 we obtain
we obtain
30a + 44b = 10 .....(i)
40a + 55b = 13 .....(ii)
By using cross-multiplication, we have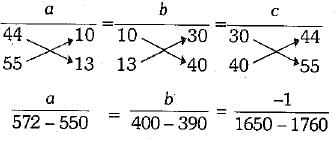
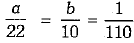
⇒ 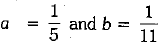
Again, putting the values of a and b, we obtain
x - y= 5 and x + y =11
Adding the two equations, we have
2x = 16 ⇒ x = 8
And x + y =11
⇒ y = 11 - 8 = 3
Hence, the speed of the boat in still water is 8 km/h.
Or
Let present age of daughter Nisha be x years
∴ Present age of Asha = (x2 + 2) years. Now, when Nisha grows to her mother’s present age, then her age would be (x2 + 2} years.
Then, her mother’s age would be
x2 + 2 + x2 + 2 - x i.e., 2x2 - x + 4
Now, as per statement of the question, we obtain
⇒ 2x2 - x + 4 = 10x - 1
⇒ 2x2 - 11x + 5 = 0
⇒ (x - 5) (2x - 1) = 0
⇒ Either x - 5 = 0 or 2x - 1 = 0
⇒ x = 5 or x = 1/2 (Rejecting)
Hence, present age of Nisha is 5 years and her mother’s age 52 + 2 i.e., 27 years.
Q.30. Prove that the parallelogram circumscribing a circle is a rhombus.
OR
Determine the values of m and n so that the following system of linear equations have infinite number of solutions: (3 Mark)
(2m - 1 ) x + 3y - 5 = 0
and 3x + (n - 1) y - 2 = 0
Solution: Let ABCD be the║ gm.
∴ AB = CD and AD = BC ...(i) 1/2
AP + PB + DR + CR = AS + BQ + DS + CQ
or, AB +C D = AD + BC
From (i), 2AB = 2AD or AB = AD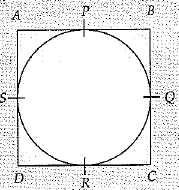
or, ABCD is a rhombus
OR
We have, for equation
(2m - l) x + 3y -5 = 0 ...(i)
a1 = 2m - 1 , b1 = 3 and c1 = - 5
and for equation
3x + (n - 1)y - 2 = 0 .....(ii)
a2 = 3, b2 = (n - 1) and c2 = -2
For a pair of linear equations to have infinite number of solutions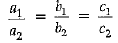
or 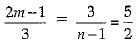
or 2(2m -1) = 15 and 5(n-1) = 6
Hence, 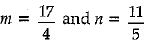
Q.31. B and C are interior angles of a triangle ABC. Show that
(i) sin 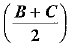 = cos A/2
= cos A/2
(ii) If ∠ A = 90°, then find the value of tan 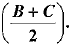 (3 Mark)
(3 Mark)
Solution: (i) A, B and C are interior angles of a triangle ABC.
∴A + B + C = 180° ....(i)
⇒ B + C = 180° - A
⇒ 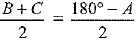
⇒ 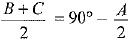
∴ 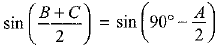
⇒ 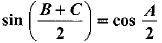 [∵ sin (90° -A) = cos A]
[∵ sin (90° -A) = cos A]
(ii) When A = 90°, from (1), we get
90° + B + C = 180°
⇒ B + C = 180° - 90° = 90°
⇒ 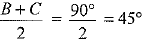
∴ 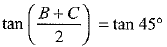
⇒ 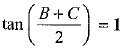
OR
If tan (A + B) = l and tan 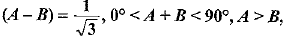 then find the values of A and B.
then find the values of A and B.
Solution: Given,
tan (A + B) = 1
⇒ tan (A + B) = tan 45°
⇒ A + B = 45° ..........(i)
and 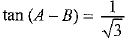
⇒ tan (A-B) = tan 30°
⇒ A - B = 30° ..........(ii)
Adding and subtracting (1) and (2), we get
2A = 75° and 2B =15°
⇒ 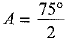 and
and 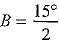
⇒ 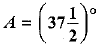 and
and 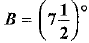
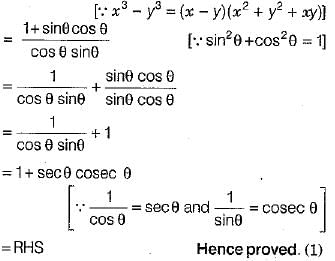
Q.32. Prove that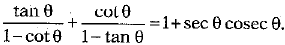
Without using trigonometric tables, evaluate the following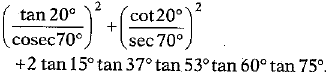 (3 Mark)
(3 Mark)
Solution: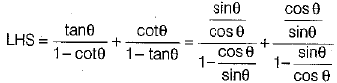
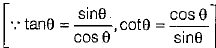
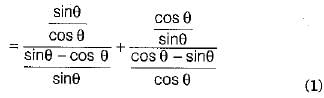
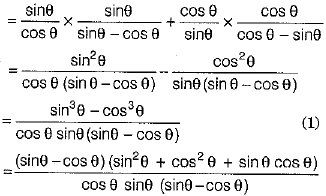
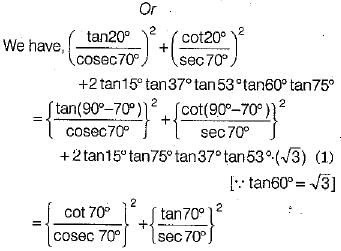
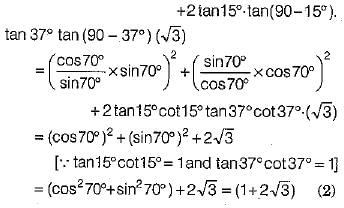
Q.33. In figure, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is 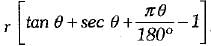 (3 Mark)
(3 Mark)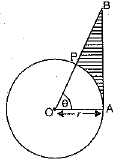
Solution: Since tangent is perpendicular to the radius at the point of contact i.e., OA ⊥ AB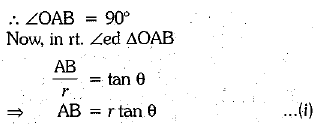

Now, the perimeter of the shaded region = AB + PB + AP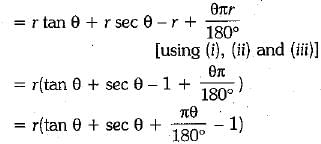
Q.34. Prove that 3 + √5 is an irrational number. (3 Mark)
Solution: Let 3 + √5 is a rational number.
∴ 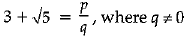
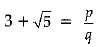
⇒ 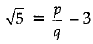
⇒ 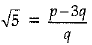
√5 is irrational and 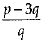 is rational (as assumed).
is rational (as assumed).
But rational number cannot be equal to an irrational number
∴3 + √5 is an irrational number.
Section D
Q.35. A pole has to be erected at a point on the boundary of a circular park of diameter 13 m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 m. Is it possible to do so ? If yes, at what distances from the two gates should the pole be erected ? (4 Mark)
Solution: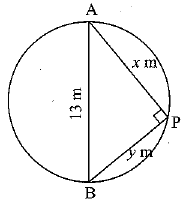
Let A and B be positions of fixed gates which are diametrically opposite in a circular park of diameter 13 m. Let P be the position of the pole such that AP = x m and BP = y m; x > y.
According to the given condition, we have
x - y = 7
⇒ x = y + 7 ...(1)
Since angle in a semi-circle is 90°
⇒ ∠APB = 90°
In right triangle ABP, we have
AP2 + BP2 =AB2 [By Pythagoras theorem]
⇒ x2 + y2 = 132
⇒ (y + 7)2 + y2 = 169 [using (1)]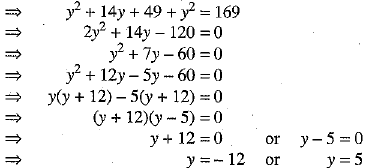
⇒ y = 5 [ ∵ y cannot be negative]
∴ x =y + 7 = 5 + 7 = 12
Hence, distances of the pole from the gates are 12 m and 5 m.
Q.36. Draw the graphs of the equations 5x - y = 5 and 3x - y = 3. Determine the coordinates of the vertices of the triangle formed by these lines and Y-axis. (4 Mark)
Solution: Given, equations are 5x - y = 5 ...(i)
and 3 x - y = 3 ..(ii)
Table for 5x - y = 5 or y = 5x - 5 is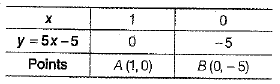
Plot the points 4(1, 0) and B( 0, - 5) on a graph paper and join these points to form a line AB. (Table for 3x- y = 3 or v = 3x - 3 is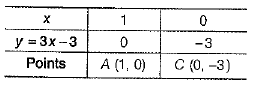
Plot the points A (1,0) and C (0, -3) on the same graph paper and join these points to form a line AC.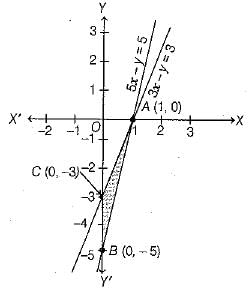
Hence, the triangle formed by given lines is ΔABC whose vertices are A(1,0),B(0, - 5) and C(0, -3).
Q.37. The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Or
The time taken by a person to cover 150 km was 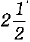 hours more than the time taken
hours more than the time taken
in the return journey. If he returned at a speed of 10 km/hour more than the speed while going, find the speed per hour in each direction. (4 Mark)
Solution: Let the larger number be x and the smaller number be y.
By the given conditions, we have
x2 - y2 =180 ...(i)
and y2 = 8x ... (ii)
From equations (i) and (ii), we have
x2 - 8x = 180
⇒ x2 - 8 x - 180 = 0
Which is a quadratic equation.
Here, a = 1, b = - 8 , c = - 180
By the quadratic formula, we have
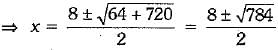
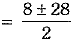
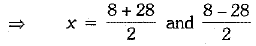
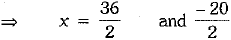
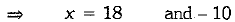
x= 18; x = - 10, it is not possible.
From equation (ii), we have
y2 = 8 x 18
⇒ y2 = 144 ⇒ y = √144 = ± 12
Hence, required numbers are 18, 12 and 18 ,- 1 2 .
Or
Let the speed of onward journey be x km/h
∴ Speed of return journey — (x + 10) km/h
Total distance = 150 km
cording to the statement of the equation, we obtain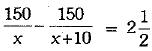
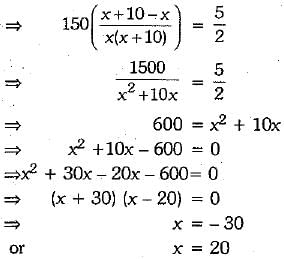
Rejecting x = - 30, because speed cannot be negative, we have x = 20
Hence, speed of onward journey is 20 km/h and speed of return journey is 20 + 10
i.e., 30 km/h.
Q.38. In figure, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP.
OR
Draw triangle ABC such that BC = 5 cm, ∠ABC = 60°, ∠ACB = 30°. Now construct ΔA'BC' corresponds to ΔABC with A'B : AB = 3 : 2. (4 Mark)
Solution: Given,
OM ⊥ PQ, bisects PQ.
PM = 8 cm (as PQ = 16 cm.)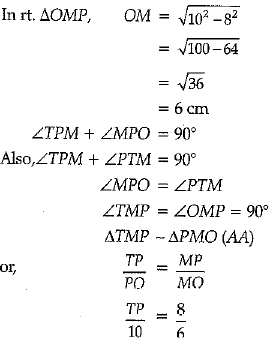
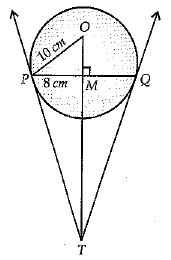
or, TP = 80/6
or, TP = 40/3
Hence length of TP = 40/3 cm.
OR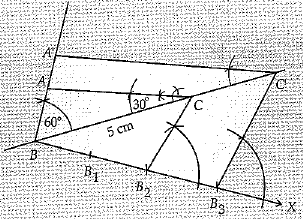
Steps of Construction:
1. Draw a line segment BC of length 5 cm.
2. Draw the angles of 60° and 30° on the points B and C respectively which intersect each other at A.
3. ΔABC is the given triangle.
4. Draw a ray BX making an acute angle with BC.
5. Locate three points B1, B2, and B3 on line segment BX. Such that BB1 = B1 B2 = B2B3.
6. Join B2C.
7. Draw 'B3C' ║ B2C to intersect the extended line BC at C'.
8. Through C draw a line parallel to AC inlersectiug extended line segment BA at A'. ΔA'BC'is the required triangle.
Q.39. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio. (4 Mark)
Solution: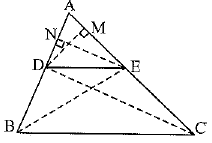
Given: A triangle ABC in which a line parallel to BC intersects other two sides AB and AC at D and E respectively.
To prove: 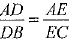
Construction: Join BE, CD and draw DM ⊥ AC and EN ⊥ AB.
Proof: Since EN is perpendicular to AB, therefore, EN is the height of triangles ADE and BDE.
∴ 
and 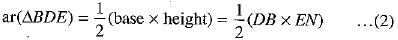
⇒ 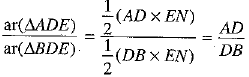 ...(3) [using (1) and (2)]
...(3) [using (1) and (2)]
Similarly, 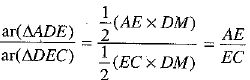 ....(4)
....(4)
Note that ΔBDE and ΔDEC are on the same base DE and between the same parallels BC and DE
∴ ar(ΔBDE) = ar(ΔDEC) ....(5)
From (4) and (5), we have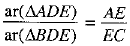 .....(6)
.....(6)
Again from (3) and (6), we have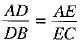
Hence, 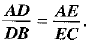
Or
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Solution: Given: A right triangle ABC, right angled at B.
To prove: (Hypotenuse)2 = (Base)2 + (Perpendicular)2
i.e., AC2 = AB2 + BC2
Construction: Draw BD ⊥ AC.
Proof: ΔADB ~ ΔABC.
In ΔADB and ΔABC
∠ADB = ∠ABC
and ∠A = ∠A
∴ . By AA-similaritv criterion, we have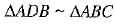
So, 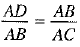 [In similar triangles, corresponding sides are proportional]
[In similar triangles, corresponding sides are proportional]
⇒ AD.AC =AB2 ..... (1)
In ΔBDC and ΔABC
∠CDB = ∠ABC [Each = 90°]
and ∠C = ∠C
∴ ABDC ~ AABC [By AA-similarity]
So, 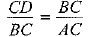 [In similar triangles, corresponding sides are proportional]
[In similar triangles, corresponding sides are proportional]
⇒ CD.AC = BC2 ...(2)
Adding (1) and (2), we have
AD.AC + CD. AC = AB2 + BC2
⇒ (AD + CD) AC = AB2 + BC2
⇒AC.AC = AB2 + BC2
Hence, AC2=AB2 + BC2
Q.40. A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7 and 8 (see the figure) and these are equally likely outcomes. (4 Mark)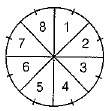
What is the probability that it will point at
(i) 8?
(ii) an odd number?
(iii) a number greater than 2?
(iv) a number less than 9?
Or
Two dice (each bearing numbers 1 to 6) are rolled together. Find the probability that the sum of the numbers on the uppei most faces of two dice is
(i) 4 or 5.
(ii) 7, 8 or 9.
(iii) between 5 and 8.
(iv) more than 10.
Solution:
∵ Total number of points on the circle = 8
(i) Let E1 = Event of getting arrow at number 8.
∴ Number of outcomes favourable to E1 = 1
Probability that arrow comes at number 8,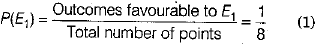
(ii) Let E2 = Event of getting arrow at an odd number
Here, odd numbers are 1,3,5 and 7.
∴ Number of outcomes favourable to E2 = 4
Probability that arrow comes at an odd number,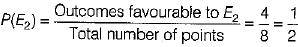
(iii) Let E3 = Event of getting arrow at a number greater than 2, i.e. at 3,4,5,6,7 or 8.
∴ Number of outcomes favourable to E3 = 6 Probability that arrow comes at a number greater than 2,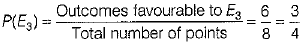
(iv) Let E4 = Event of getting arrow at a number less than 9.
∴ Number of outcomes favourable to E4 = 8
Probability that arrow comes at a number less than 9,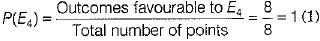
Or
Total number of possible outcomes on rolling two dice together = 36
(i) To get the sum of numbers, 4 or 5, favourable outcomes are (1,3), (3, 1), (2, 2), (1,4), (4, 1), (2, 3) and (3, 2).
∴ Number of favourable outcomes = 7
Now, P (getting a sum 4 or 5) = 7/36
(ii) To get the sum of numbers, 7, 8 or 9, favourable outcomes are (1,6), (6,1), (2,5), (5, 2), (3, 4), (4, 3), {2, 6), (6, 2), (3, 5), (5, 3), (4, 4), {3, 6), (6, 3), (4, 5) and (5, 4).
∴ Number of favourable outcomes = 15
Now, P (getting a sum 7, 8 or 9) = 
(iii) To get the sum of numbers, between 5 and 8, i.e. getting sum 6 or 7, favourable outcomes are (1, 5), (5,1), (2, 4), (4, 2), (3,3), (1,6), (6,1), {2, 5), (5, 2), (3, 4) and (4, 3).
Number of favourable outcomes = 11 Now. P faettina a sum between 5 and 8)
= 11/36
(iv)To get the sum of numbers more than 10, i.e. getting sum 11 or 12, favourable outcomes are (5, 6), (6, 5) and (6, 6).
∴ Number of favourable outcomes = 3
Now, P (getting a sum more than 10)
= 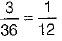
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 3 - Mathematics (Maths) Class 10
| 1. How can I access the CBSE Sample Question Paper for Class 10 Mathematics (2019-20)? |  |
| 2. Is the CBSE Sample Question Paper for Class 10 Mathematics (2019-20) the same as the actual exam paper? |  |
| 3. Are the solutions provided for the CBSE Sample Question Paper for Class 10 Mathematics (2019-20)? |  |
| 4. Can I use the CBSE Sample Question Paper for Class 10 Mathematics (2019-20) for other boards as well? |  |
| 5. How can I make the most of the CBSE Sample Question Paper for Class 10 Mathematics (2019-20) to prepare for the exam? |  |





















