Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 5 | CBSE Sample Papers For Class 10 PDF Download
Class X
Mathematics – Standard (041)
Sample Question Paper 2019-20
Max. Marks: 80
Duration : 3 hrs
General Instructions:
(i) All the questions are compulsory.
(ii) The question paper consists of 40 questions divided into 4 sections A, B, C, and D.
(iii) Section A comprises of 20 questions of 1 mark each. Section B comprises of 6 questions of 2 marks each. Section C comprises of 8 questions of 3 marks each. Section D comprises of 6 questions of 4 marks each.
(iv) There is no overall choice. However, an internal choice has been provided in two questions of 1 mark each, two questions of 2 marks each, three questions of 3 marks each, and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
(v) Use of calculators is not permitted.
Section A
Q.1. If sin x + cos y = 1; x = 300 and y is an acute angle, find the value of y. (1 Mark)
(a) 600
(b) 700
(c) 560
(d) 500
Ans. Choice (a) is correct.
Given,
sin x + cos y = 1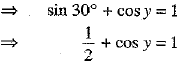
⇒ 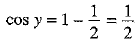
⇒ cos y = cos 600
⇒ y = 600
Q.2. If ΔABC is an isosceles triangle, right angled at C, with AC = 2 cm, then the hypotenuse is equal to (1 Mark)
(a) 2 cm
(b) 2√2 cm
(c) 2 + √2 cm
(d) 4 cm
Ans. (b) Given, ΔACB right angled at C.
We have, AC = CB = 2 cm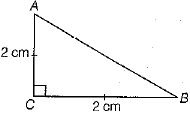
By Pythagoras theorem,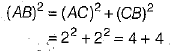
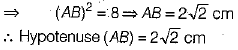
Q.3. If the first observation is increased by 1, the second by 2, the third by 3, and so on of n observations of a data, whose mean is  then the new mean is: (1 Mark)
then the new mean is: (1 Mark)
(a) 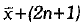
(b) 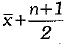
(c) 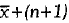
(d) 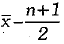
Ans. (b) 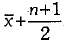
[Here, new mean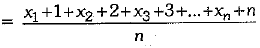
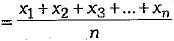
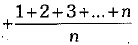
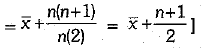
Q.4. A pole 6 m high casts a shadow 2√3 m long on the ground, then the Sun's elevation is: (1 Mark)
(a) 600
(b)450
(c) 300
(d) 900
OR
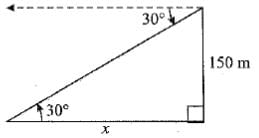
The angle of depression of a car parked on the road from the top of 150 m high tower is 300. The distance of the car from the tower (in metres) is:
(a) 50√3
(a) 150√3
(a) 150√2
(a) 75
Ans. (a) Explanation: In ΔABC, ∠B = 900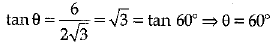
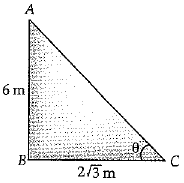
OR
(b) Explanation: In ΔABC, ∠B = 900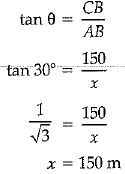
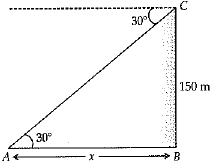
Q.5. The angle of depression of a car parked on the road from the top of the 150 m high tower is 300. The distance of the car from the tower is (1 Mark)
(a) 50√3 m
(b) 150√3 m
(c) 150√2 m
(d) 75 m
Ans. Choice (b) is correct.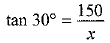
⇒ 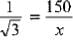
⇒ x = 150√3 m
Q.6. If a = 2 and 20th term = 62, then sum of first 20 terms of an AP is (1 Mark)
(a) 590
(b) 620
(c) 640
(d) 660
Ans. (c) Given, a = 2, a20 = 62 and n = 20
Now, sum of first 20 terms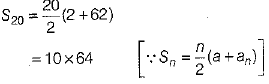
= 640
Q.7. If 5β and 4β are acute angles satisfying sin 5β = cos 4β, then 2 sin 3β - √3 tan 3β is: (1 Mark)
(a) 1
(b) -1
(c) 0
(d) 1+√3
Ans. (c) [Given that sin 5β = cos 4β,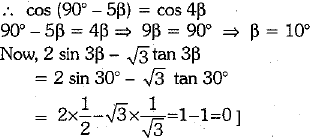
Q.8. If the common difference of an A.E, is 5, then what is a18 - a13? (1 Mark)
(a) 5
(b) 20
(c) 25
(d) 30
Ans. (c)
Explanation: In the given A.P., d = 5 Thus,
a18 - a13 = a + 17d - a - 12d = 5d = 25
Q.9. If cot 3θ = sin 450.cos 450 + cos 600, thenθ is __________ . (1 Mark)
Ans. 150
We have,
cos 3θ = sin 450.cos 450 + cos 600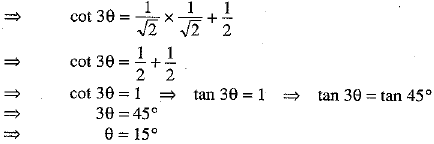
Q.10. The value of k for which the system of equations x + ky = 0 , 2 x - y = 0 has unique solution is (1 Mark)
(a) -1/3
(b) Other than -1/2
(c) -1/4
(d) Other than -1/4
Ans. (b) Given system of equations is
x + ky = 0 and 2x - y = 0
On comparing these equations with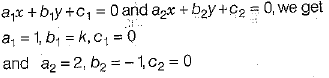
Condition for unique solution,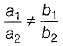
⇒ 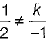
⇒ 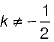
Q.11. The maximum value of a cone that can be carved out of a solid hemisphere of radius r is _________. (1 Mark)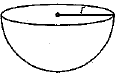
Ans. 1/3πr3 cubic units.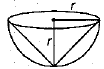 [Here, radius of the base
[Here, radius of the base
= height of the cone = r
∴ Volume of the cone
Q.12. Find a rational number between √2 and √3. (1 Mark)
Ans. Since,
√2 = 1.414
and √3 = 1.732
Now, we can write 'n' rational number between those e.g., just greater than 1.414 and less than 1.732 and it should be terminating or not
e.g.,: 1.415659,1.416893,1.715644, ...
Therefore, one rational number between √2 and √3 is 1.416893.
Q.13. cosec 300 + tan 450 - 1 = 2 (1 Mark)
Ans. True.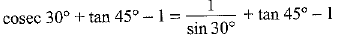
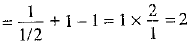
Q.14. The distance between the points A(x1, y1) and B (x2, y2) is given by ______. (1 Mark)
Ans. 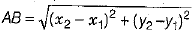
Q.15. A number is selected at random from the numbers 3, 5, 5, 1, 7, 7, 9, 9, 9, 9. Then probability that the selected number is their average = _______. (1 Mark)
Ans. 7/10
[Average of given ten numbers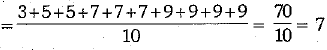
Required probability = 7/10]
Q.16. Is series √3, √6, √9, √12 , .... an A.P.? Give reason. (1 Mark)
Ans. Common difference,
d = √6-√3
= √3(√2-1)
Again, d = √9-√6
= 3-√6
= √12-√9 = 2√3-3
As common difference are not equal.
Hence, the given series is not in A.P.
Q.17. Given below is a cumulative frequency distribution of dess than type’: (1 Mark)
| Marks obtained | Less than 10 | Less than 20 | Less than 30 | Less than 40 | Less than 50 |
| Number of students | 4 | 7 | 18 | 33 | 40 |
Change the above data into a continuous grouped frequency distribution.
Ans. Changing given cumulative frequency distribution into continuous grouped frequency distribution, we get
| Class interval | Frequency |
| 0-10 | 4 |
| 10-20 | 7-4 = 3 |
| 20-30 | 18-7 = 11 |
| 30-40 | 33-18 = 15 |
| 40-50 | 40-33 = 7 |
Q.18. Which term of the AP: 21, 18,15,... is -81? (1 Mark)
Ans. Given, AP is 21, 18, 15, ...
Here, a = 21 and d = 18 - 21 = -3
Let nth term of given AP be -81.
Then, an = -81
⇒ a + [n-1)d = -81 [∴an = a + (n-1)d]... (i)
On putting the values of a and d in Eq. (i), we get
21 + (n -1) x (-3)= -81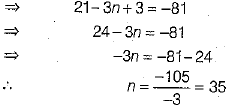
Hence, 35th term of given AP is -81.
Q.19. Which constant must be added and subtracted to solve the quadratic equation 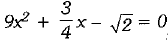 by the method of completing the square? (1 Mark)
by the method of completing the square? (1 Mark)
Ans.
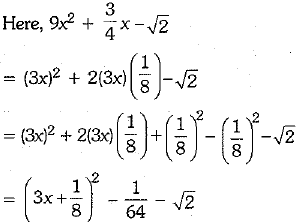
Hence, the required constant added and subtracted is 1/64.
Q.20. If A and B are acute angles and sin A = cos B, then find the value of A + B. (1 Mark)
Ans. Given, sin A = cos B
Or, sin A = sin (900 - B)
or, A = 900 - B
∴ A + B = 900
SECTION B
Q.21. If Sn, the sum of the first n terms of an A.P. is given by Sn = 2n2 + n, then find its nth term.
OR
If the 17th term of an A.P. exceeds its 10th term by 7, find the common difference. (2 Mark)
Ans. Given, Sn= 2n2 + n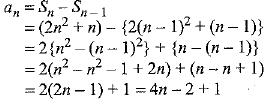
⇒ an = 4n - 1
OR
Let an denote nth term of A.P. with first term, a and common difference d. According to given condition, we have
a17-a10 = 7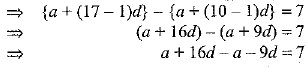
⇒ 7d = 7
⇒ d = 1
Hence, the common difference, d is 1.
Q.22. If one root of the quadratic equation 2x2 + kx - 6 = 0 is 2, find the value of k. Also, find the other root. (2 Mark)
Ans. Since, x = 2 is a root of the equation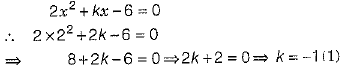
On putting k = -1 in the equation 2x2 + kx - 6 = 0,
we get,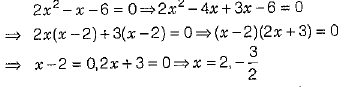
Hence, the other root is - 3/2.
Q.23. In trapezium ABCD, AB || DC, DC = 2AB, EF drawn parallel to AB cuts AD in F and BC in E such that 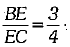 Diagonal DB intersects EF at G. Prove that 7EF = 10AB.
Diagonal DB intersects EF at G. Prove that 7EF = 10AB.
OR
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides. (2 Mark)
Ans. In ΔDFG and ΔDAB, we have
∠l = ∠2 [∴ AB || DC || EF ∴∠and ∠2 are corresponding angles]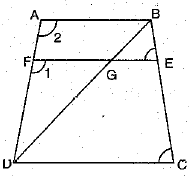
∠FDG = ∠ADB [common]
So, by AA criterion of similarity, we have
ΔDFG ∼ ΔDAB
⇒ 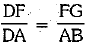 ...(i)
...(i)
In trapezium ABCD, we have EF || AB || DC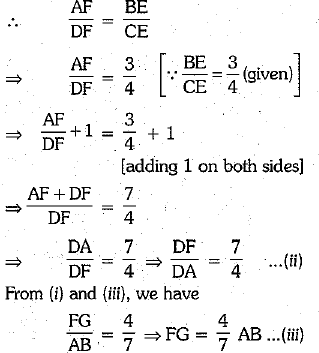
In ΔBEG and ΔBCD, we have
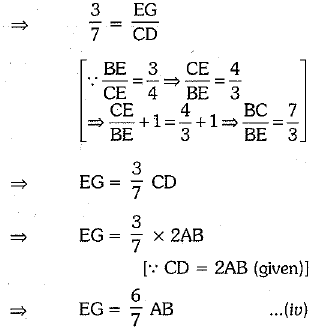
Adding (iii) and (iv), we have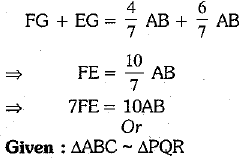

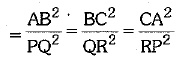
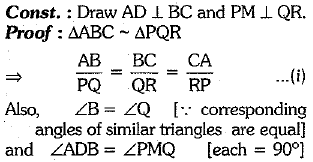
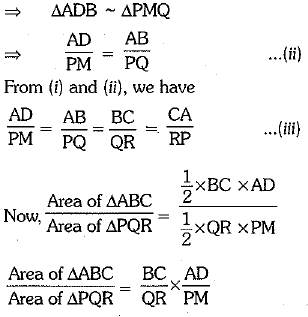

Q.24. Find the 7th term from the end of A.E 7, 10, 13, ....... 184. (2 Mark)
Ans. Let us write A.E in reverse order
i.e., 184,........ 13,10,7.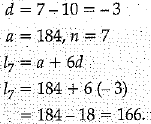
Hence, 166 is the 7th term from the end.
Q.25. Cards marked with numbers 5 to 50 (one number on one card) are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that the number on the card taken out is (i) a prime number less than 10, (ii) a number which is a perfect square. (2 Mark)
Ans. A card is drawn at random from a box containing cards numbered from 5 to 50.
It can be drawn in 46 different ways.
∴ Total number of possible outcomes = 46
(i) Let E be the event that card drawn from the box has a prime number less than 10.
The prime numbers less than 10 are 5, 7.
These are 2 numbers.
∴ Number of cases in favour of event E = 2
Probability of getting a card having a prime number less than 10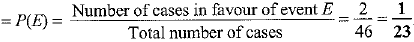
(ii) Let F be the event that card drawn from the box has a perfect square.
The perfect square numbers from 5 to 50 are 9, 16, 25, 36, 49.
These are 5 numbers.
∴ Number of cases in favour of event F = 5
Probability of getting a card having a perfect square number from 5 to 50.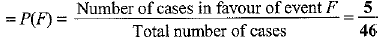
Q.26. Find the ratio in which the line segment joining A(1, - 5) and B(-4, 5) is divided by the X-axis.
OR
Find the coordinates of points on the X-axis which are at the distance of 17 units from the point (11, - 8). (2 Mark)
Ans. For any point on X-axis, y = 0.
Let the ratio be k : 1, then by section formula, the coordinates of the point which divides AB in the ratio k : 1 are 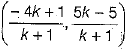
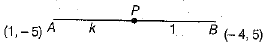
Thus, point lies on the X-axis, and we know that on the X-axis, the ordinate is zero.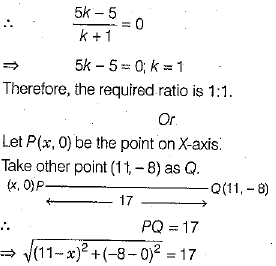
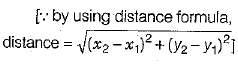
On squaring both sides, we get
(11- x)2 + (-8)2 = 289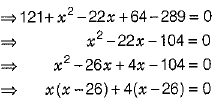
SECTION C
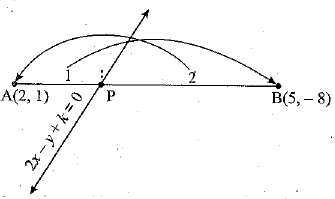
Q.27. Point P divides the line segment joining the points A(2, 1) and P(5, -8) such that 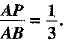 If P lies on the line 2x - y + k = 0, find the value of k.
If P lies on the line 2x - y + k = 0, find the value of k.
OR
For what value of p, are the points (2,1), (p,-1) and (-1,3) collinear? (3 Mark)
Ans. Given points are A (2, 1) and B(5, - 8).
It is given that 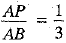
⇒ 3AP=AP
⇒ 3AP=AP + PB
⇒ 2AP = PB
⇒ 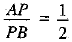
⇒ AP : PB = 1 : 2
Therefore, point P divides AB in the ratio 1 : 2.
Using section formula, the coordinates of point P are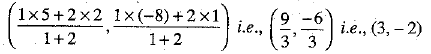
Hence, the coordinates of P are (3, -2).
Point P(3, -2) lies on the line given by the equation
2x-y+k = 0
∴ The coordinates of point P satisfies above equation.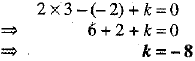
OR
Let the given points be A(2,1), B(p, -1) and C(-1, 3). Since the points A(2, 1), B(p, -1) and C(-1, 3) are collinear, therefore, the area of the triangle formed by them is zero.
∴ Area of ΔABC = 0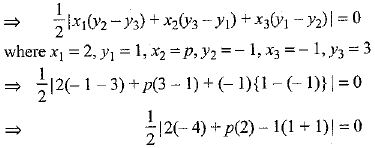
⇒ 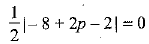
⇒ |2p - 10| = 0
⇒ 2p - 10 = 0
⇒ p = 5
Hence, the given points are collinear when p = 5.
Q.28. Show that one and only one out of n, n + 3, n + 6 or n + 9 is divisible by 4. (3 Mark)
Ans. Let us apply the division algorithm with a = n and b = 4, we get
n = 4q +r, 0 ≤ r < 4
⇒ n = 4q + r, where r can have one and only one value of 0, 1, 2 or 3.
⇒ n = 4q or 4q + 1, or 4q + 2, or 4q + 3 and one and only one of these above possibilities can happen.
(i) If n = 4q, then n is divisible by 4.
(ii) If n = 4q + 1, then n + 3 = 4q + 4 = 4(q +1), therefore n + 3 is divisible by 4.
(iii) If n = 4q + 2, then n + 6 = 4q + 8 = 4(q + 2), therefore n + 6 is divisible by 4.
(iv) If n = 4q + 3, then n + 9 = 4q + 12 = 4(q + 3), therefore n + 9 is divisible 4.
Q.29. Solve the following pair of equations: (3 Mark)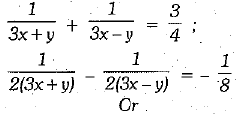
A boat goes 24 km upstream and 28 km downstream in 6 hours. If goes 30 km upstream and 21 km downstream in  hours. Find the speed of boat in still water and also speed of the stream.
hours. Find the speed of boat in still water and also speed of the stream.
Ans. 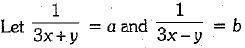
∴ Given pair of equations can be rewritten as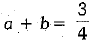 ...(i)
...(i)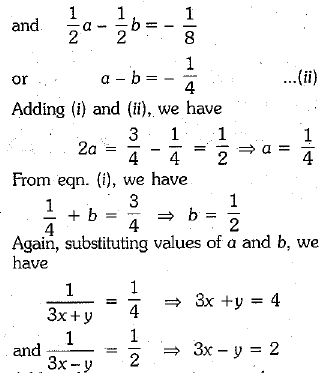
Adding these two equations, we have
6x = 6 ⇒ x = 1
And 3(1) + y = 4 ⇒ y = 1
Hence, the values of x and y are x = 1, y = 1.
OR
Let speed of the boat in still wafer be x km/h and speed of the stream be y km/h. In case of downstream, effective speed of the boat = (x + y) km/h.
In case of upstream, effective speed of the boat = (x - y) km/h
According to the statement of the question, we have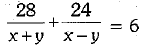
and 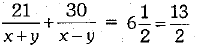
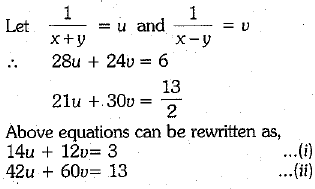
Multiplying equation (i) by 5, we have
Solving (iii) and (iv), we have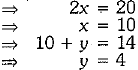
Hence, speed of boat in still water = 10 km/h and speed of the stream
= 4 km/h.
Q.30. If 4 tanθ = 3, evaluate (3 Mark)
OR
An electric pole is 12 m high. A steel wire tied to top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 600 with the horizontal through the foot of the pole, find the length of the wire.
Ans. Given, 4 tanθ = 3
⇒ tanθ = 3/4
⇒ sinθ = 3/5 and cosθ = 4/5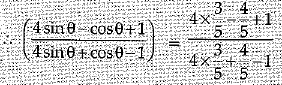
= 13/11
OR
Let OA be the electric pole and B be the point on the ground to fix the wire.
Let BA be x m.
In ΔABO, AO/AB = sin600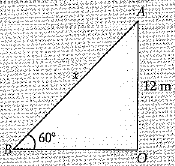
⇒12/x = √3/2
⇒ 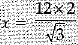
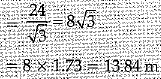
Hence, the length of wire = 13.84 m.
Q.31. In ΔABC, ∠B = 900 and D is the mid - point of BC. prove that AC2 = AD2 + 3CD2. (3 Mark)
OR
In figure, E is a point on CB produced of an isosceles ΔABC, with side AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ~ ΔECF.
Ans. Given in ΔABC, ∠B = 900 and D is the mid-point of BC.
BD = CD = BC/2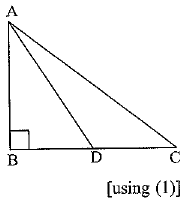 ⇒ BC = 2 CD ...(1)
⇒ BC = 2 CD ...(1)
In right triangle ABC, right angled at B, we have
AC2=AB2 + BC2 ...(2)
In right triangle ABD, right angled at B, we have
AD2=AB2 + BD2 ...(3)
Subtracting (3) from (2), we have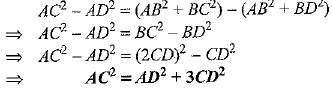
OR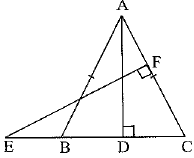
It is given that AABC is an isosceles with AB - AC.
∴ ∠C = ∠B
Now, in triangles ABD and ECF, we have
∠ABD = ∠ECF [∴ ∠B - ∠C]
∠ADB = ∠EFC = 900 [∵ AD ⊥ BC and EF ⊥ AC]
So, by AA-criterion of similarity, we have
ΔABD ~ ΔECF
Q.32. Prove that (3 Mark)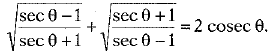
OR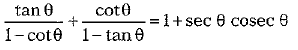
Ans. 
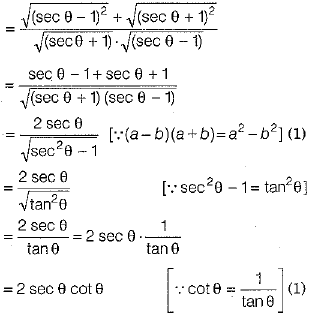
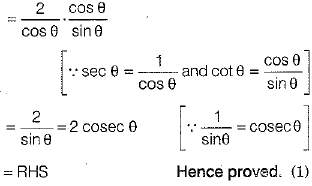
OR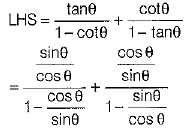
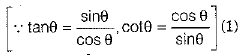
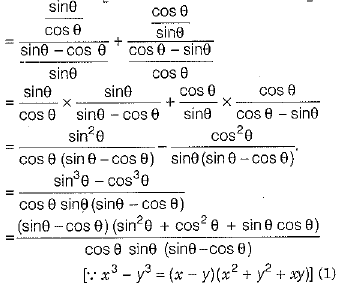
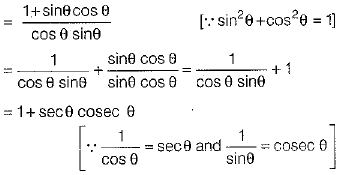
= RHS
Q.33. In figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of in tersection O of the diagonals of the square lawn, find the sum of the area of the lawn and the flower beds. (3 Mark)
Ans. ∵The diagonals of the square are perpendicular bisector of each other.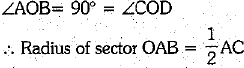
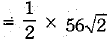
= 28√2 m [∵ Diagonal of square = √2 x side]
Also, radius of sector COD = 28√2m
∴ Area of (sector AOB + sector COD)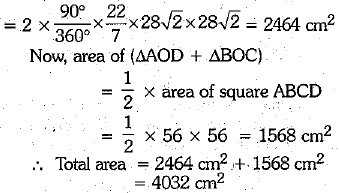
Q.34.In the figure, ΔACB is in the semi-circle. Find the area of shaded region given that AB = 42 cm.
OR
The largest possible sphere is cut out from a wooden solid cube of side 7 cm. Find the volume of the wood left.  (3 Mark)
(3 Mark)
Ans.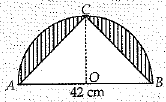
Base of triangle = diameter of semicircle
= 42 cm
and its height - radius of semicircle
= 42/2 = 21 cm
Area of shaded portion = Area of semicircle - area of ΔABC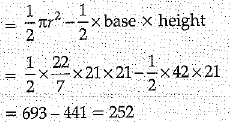
Hence, the area of shaded portion = 252 cm2.
OR
Given, the side of cube a = 7 cm
Since, the diameter of the largest possible sphere = Side of the cube
Hence, the radius of sphere = 7/2 cm.
Volume of the wood left = Volume of cube - Volume of sphere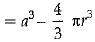
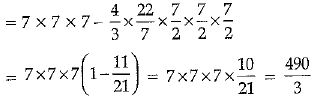
Hence, Volume of wood left = 163.3 cm3.
SECTION D
Q.35. A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 h less for the same journey. Find the speed of the train. (4 Mark)
OR
Solve for x :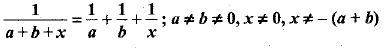
Ans. Let the usual speed of the train be x km/h. Then,
Time taken to cover 360 km with usual speed = 360/x h
If the speed had been increased by 5 km/h, then increased speed = (x + 5) km/h
Time taken to cover 360 km with increased speed 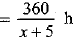
∴ According to the given condition in the question, we have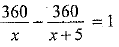
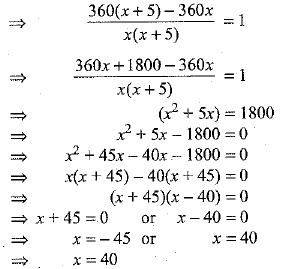
Hence, the usual speed of the train is 40 km/h.
OR
The given equation is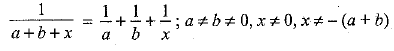
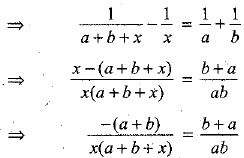
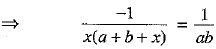 [On dividing by (a + b)]
[On dividing by (a + b)]
Cross-multiplying, we get
x(x + a + b) = - ab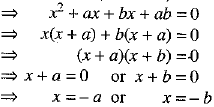
Hence, the roots of the equation be - a and - b.
Q.36. 216 logs are stacked in the following manner as 21 logs in the bottom row, 20 in the next row, 19 in the next row to it and so on (see the figure). In how many rows are the 216 logs placed and how many logs are in the top row? (4 Mark)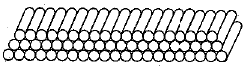
Ans. Here, logs stacked in each row form a series
21 + 20 + 19 + 18 + 17 + ...
which is in AP with first term, a = 21 and common difference, d = 20 - 21 = -1.
Let the number of rows be n, then Sn = 216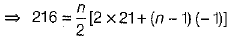
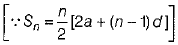
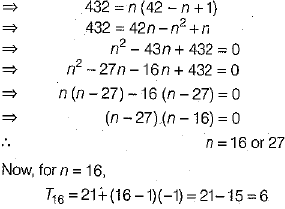
and for n = 27,
T27 =21 + (27 - 1)(-1)=21-26 = -5
which is not possible.
[∴ number of logs in any row cannot be negative]
So, the number of rows is 16 and number of logs in the top row = 6.
Q.37. A and B working together can do α piece of work in 6 days. If A takes 5 days less than B to finish the work, in how many days B alone can do the work?
OR
Sum of the areas of two squares is 468m2, If the difference of their perimeters is 24m, find the sides of the two squares. (4 Mark)
Ans. Let B takes x days to finish the work and A takes (x - 5) days to finish the same work.
A's one day work + B’s one day work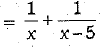
But (A + B)’s one day work = 1/6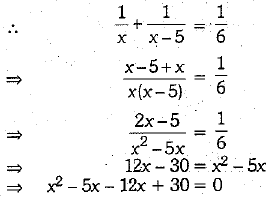
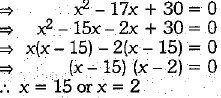
But x can rtot be less than 6. So, B alone can finish the work in 15 days.
OR
Let the side of first square be x m and the side of second square be y m.
Then, the area of first square = x2 m2
and the area of second square = y2 m2
Perimeter of the first square = 4x m
and perimeter of the second square = 4y m Now, according to the given statement, we have
x2 + y2 = 468 ...(i)
and 4x - 4y = 24
⇒ x - y = 6 ...(ii)
From equation (ii), we have x = 6 + y ...(iii)
Putting this value of x in (i), we have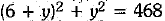
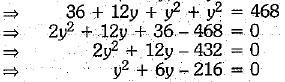
which is a quadratic equation in y.
We can solve this equation by quadratic formula.
Here, a = 1, b = 6, c = - 216
∴ D = b2- 4 ac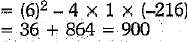
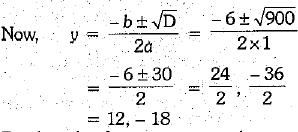
But the side of a square cannot be -ve.
∴ y = 12
Putting this value of y in (iii), we have x = 6 + 12 = 18
Hence, the side of the first square is 18 m and the side of the second square = 12 m.
Q.38. A man on the top of a vertical observation tower observes a car moving at uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 300 to 450, how long will the car take to reach the observation tower from this point? (4 Mark)
OR
Prove that: 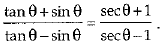
Ans. Let the speed of car by x m/minutes
In ΔABC,
h/y = tan 450
⇒ h = y
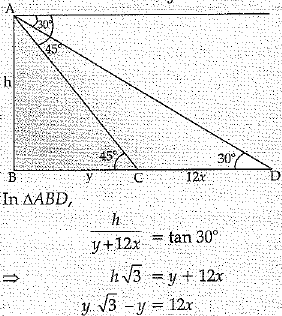
Hence, time taken from C to B = 6(√3+1) minutes
OR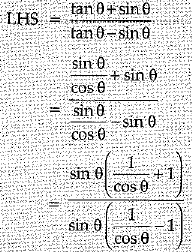
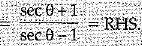
Q.39. Find the values of frequecies x and y in the following frequency distribution table, if N = 100 and median is 32. (4 Mark)
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | Total |
| No. of students | 10 | x | 25 | 30 | y | 10 | 100 |
OR
For the following frequency distribution, draw a cumulative frequency curve (ogive) of ‘more than type’ and hence obtain the median value.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| Frequency | 5 | 15 | 20 | 23 | 17 | 11 | 9 |
Ans. We have,
Median = 32 and N= 100
We prepare cumulative frequency table to calculate median: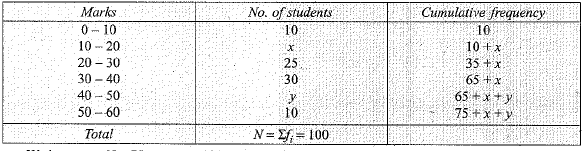
We have, N = 75 + x + y = 100
⇒ x + y = 25 ...(1)
Given, median = 32, so that median class is 30-40.
l = lower limit of the median class = 30, f = frequency of the median, class = 30,
h = width of the median class = 10, cf = cumulative frequency o f the class just preceding the median class = 35 + x.
Using the formula: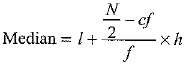
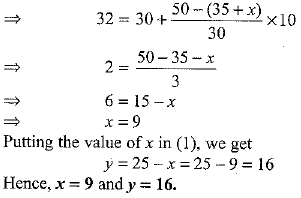
OR
We prepare the cumulative frequency table by more than type method as given below:
Here, 0, 10, 20, 30, 40, 50, 60 are the lower limits of the respective class interval 0 - 10, 10 - 20, 20 - 30, 30 - 40, 40 - 50, 50 - 60, 60 - 70. To represent the data in the table graphically, we mark the lower limits of the class interval on the horizontal axis (x-axis) and their corresponding cumulative frequencies on the vertical axis (y-axis), by choosing a convenient scale. Other than the given class intervals, we assume the class interval 70 - 80 succeeding to the last class mark 60 - 70 with zero frequency. Now, plot the points (0, 100), (10, 95), (20, 80), (30, 60), (40, 37), (50, 20), (60, 9) and (70, 0) on a graph paper and join them by a free hand smooth curve. This curve is called an ogive more than type (see figure).
Mark N/2 = 100/2 = 50 on the y-axis.
From the point, draw a line parallel to x-axis cutting the curve at a point P. From this point P, draw a perpendicular to the x-axis. The point of intersection M of this perpendicular with the x-axis determines the median of the given data.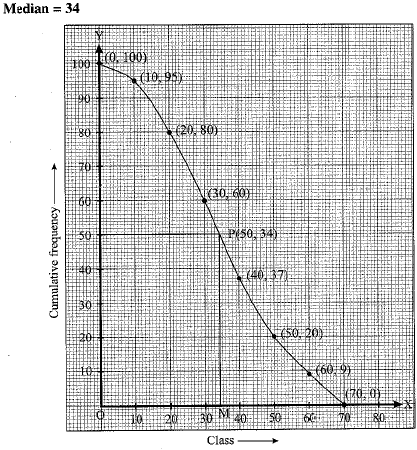
Q.40. From a well-shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is
(i) a queen of black colour.
(ii) a card with number 5 or 6.
(iii) a card with number less than 8.
(iv) a card with number between 2 and 9. (4 Mark)
Ans. Since, one card is drawn from 52 well-shuffled cards,
∴ Total number of possible outcomes = 52
(i) Since, there are 2 queens of black colour.
∴ P (getting a queen of black colour)
= 2/52 = 1/26
(ii) In each suit, there are 2 cards with number 5 and 6. So, total such ca rd s are 4 tim es 2 = 8
∴ P (getting a card with number 5 or 6)
= 8/52 = 2/13
(iii) In each suit, there are 6 cards with number less than 8, namely 2, 3, 4, 5, 6 and 7
∴ P (getting a card with number less than 8)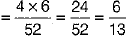
(iv) In each suit, there are 6 cards with number between 2 and 9, namely 3, 4, 5, 6, 7,8.
∴ P( getting a card with number between 2 and 9) 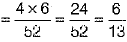
|
303 docs|7 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 5 - CBSE Sample Papers For Class 10
| 1. What is the format of the CBSE Sample Question Paper for Class 10 Mathematics? |  |
| 2. How can I effectively prepare for the Class 10 Mathematics exam using the CBSE Sample Question Paper? |  |
| 3. Are the questions in the CBSE Sample Question Paper for Class 10 Mathematics similar to the ones asked in the actual board exam? |  |
| 4. Is it necessary to solve the CBSE Sample Question Paper for Class 10 Mathematics even if I have already completed my textbook? |  |
| 5. Can I rely solely on the CBSE Sample Question Paper for Class 10 Mathematics for exam preparation? |  |

|
Explore Courses for Class 10 exam
|

|

















