Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 6 | CBSE Sample Papers For Class 10 PDF Download
Class X
Mathematics – Standard (041)
Sample Question Paper 2019-20
Max. Marks: 80
Duration : 3 hrs
General Instructions:
(i) All the questions are compulsory.
(ii) The question paper consists of 40 questions divided into 4 sections A, B, C, and D.
(iii) Section A comprises of 20 questions of 1 mark each. Section B comprises of 6 questions of 2 marks each. Section C comprises of 8 questions of 3 marks each. Section D comprises of 6 questions of 4 marks each.
(iv) There is no overall choice. However, an internal choice has been provided in two questions of 1 mark each, two questions of 2 marks each, three questions of 3 marks each, and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
(v) Use of calculators is not permitted.
Section A
Q.1. If the HCF of 65 and 117 is expressible in the form 65m - 117, find the value of m : (1 Mark)
Ans. By the Euclid's division algorithm, HCF of (65, 117) = 13
Since 65m - 117 = 13 ⇒ m = 2
Q.2. Consider the following frequency distribution of the heights of 60 students of a class (1 Mark)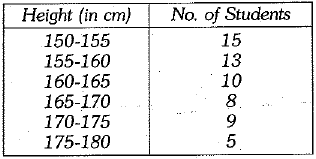
The upper limit of the median class in the given data is:
(a) 165
(b) 160
(c) 155
(d) 170
Ans. (a) 165 [Here, the median class is 160-165]
Q.3. The equations x + 2y + 5 = 0 and - 3x - 6y + 1 = 0 has (1 Mark)
(a) exactly two solutions
(b) infinitely many solutions
(c) no solution
(d) a unique solution
Ans.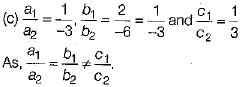
Hence, the given system has no solution.
Q.4.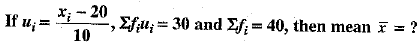 (1 Mark)
(1 Mark)
(a) 70
(b) 50.5
(c) 27.5
(d) 20.5
Ans. (c)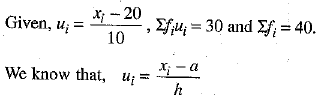
On comparing, we get
a = 20 and h = 10
∴ 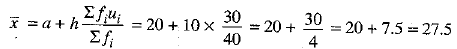
Q.5. The point which divides the line segment joining the points (7, -6) and (3, 4) in ratio 1:2 internally lies in the : (1 Mark)
(a) I quadrant
(b) II quadrant
(c) III quadrant
(d) IV quadrant
Ans. (d)
Let (x, y) be the point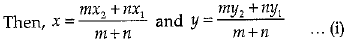
Here, x1 = 7, y1 = -6, x2 = 3, y2 = 4, m = 1 and n = 2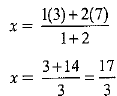
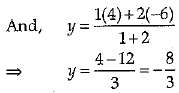
So, the required point  lies in IVth quadrant.
lies in IVth quadrant.
Q.6. If sin θ + cos θ =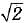 cos θ, (θ ≠ 90°), then the value of tan θ is : (1 Mark)
cos θ, (θ ≠ 90°), then the value of tan θ is : (1 Mark)
(a)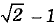
(b) 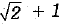
(c) 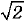
(d) 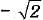
Ans. (a)
Q.7. If the HCF of 65 and 117 is of the form (65m -117), then m =? (1 Mark)
(a) 2
(b) 3
(c) 13
(d) 5
Sol. (a) HCF (65,117) = 13
⇒ 65m - 117 = 13 ⇒ 65m = 130
∴ m = 2
Q.8. In the given figure, if ST║QR and PS : PQ = 2 : 5 and TR = 15 cm, then PT =_______. (1 Mark)
Ans. It is given that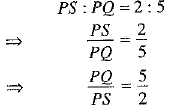
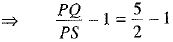 [Subtracting ‘1’ from both sides]
[Subtracting ‘1’ from both sides]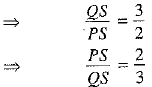

In ΔPQR, ST║QR.
∴ By Basic Proportionality Theorem
⇒ 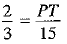 [using (1), TR = 15 cm (given)]
[using (1), TR = 15 cm (given)]
⇒ 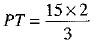
⇒ PT = 10 cm
Q.9. Area of the largest triangle that can be inscribed in a semi-circle of radius 'r' units is : (1 Mark)
(a) r2 sq. units
(b) 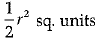
(c) 2r2 sq. units
(d) 
Or
A cylindrical pencil sharpened at one edge is the combination of :
(a) a cone and a cylinder
(b) frustum of a cone and a cylinder
(c) a hemisphere and a cylinder
(d) two cylinders
Ans. (a)
Take a point C on the circumference of the semi-circle and join it by the end points of diameter AB.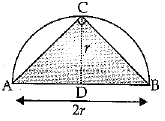
∠C = 90° [Angle in a semi-circle is right angle]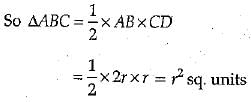
Or
Correct option: (a)
The sharpened part of the pencil is cone and unsharpened part is cylinder.
Q.10. 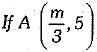 is the mid-point o f the line segment joining the points Q (- 6, 7) and R (-2, 3), then the value of m is : (1 Mark)
is the mid-point o f the line segment joining the points Q (- 6, 7) and R (-2, 3), then the value of m is : (1 Mark)
(a) - 12
(b) - 4
(c) 12
(d) - 6
Ans. (a)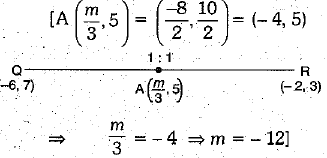
Q.11. cot (90 - θ) is equal to_______. (1 Mark)
Ans. tan θ
Q.12. If st number of circles touch a given line PQ at a point A, then their centres lie on the perpendicular bisector of PQ. (1 Mark)
Ans. False
Q.13. Find the value of c for which the pair of equations cx - y = 2 and 6x - 2y = 3 will have infinitely many solutions. (1 Mark)
Or
Find the roots of the quadratic equation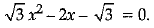
Ans. For infinitely many solutions,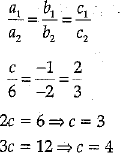
As from the ratios, values of c are not common. So, there is no common value of c for which lines have infinitely many solutions.
Or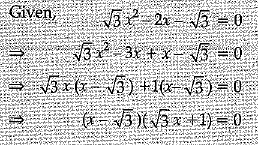
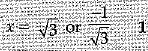
Q.14. Fill the two blanks in the sequence 2,........, 26, ...... so that the sequence forms an AP. (1 Mark)
Ans. 14, 38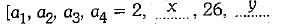
Now, a + d = x
and a2 + d = 26, a3 + d = y
2 + d = x
x + d = 26, 26 + d = y
2 + d + d = 26, 26 + 12 = y
⇒ d = 12
Hence, 2 + 12 = 14 = x and 26 + 12 = 38 = y
Q.15. All equilateral triangles are ________.
Or
Two triangles are similar, if their corresponding sides are ______. (1 Mark)
Ans. Similar
Or
Proportional
Q.16. Find a rational number between  (1 Mark)
(1 Mark)
Ans. A number written as terminating decimal will always be rational.
∴ 1.42 (terminating decimal) lies between 1.41 and 1.73 i.e., 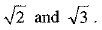
Q.17. In the given figure, AOB is a diameter of the circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, then find ∠ACO. (1 Mark)
Ans.
∠OAC = 90° (as radius ⊥ tangent)
∠BOC = ∠OAC + ∠ACO
(Exterior angle property)
or, 130° = 90° + ∠ACO
or, ∠ACO = 130° - 90° = 40°
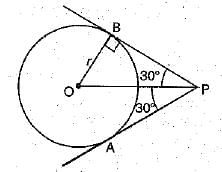
Q.18. If the angle between two tangents drawn from an external point ‘P’ to a circle of radius Y and centre O is 60°, then find the length of OP.
Or
If the radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle. (1 Mark)
Ans. Since OP bisects ∠BPA

Q.19. What is the nature of roots of the quadratic equation 5y2 - 4y + 3 = 0. (1 Mark)
Ans. Given, quadratic equation is 5y2 - 4y + 3 = 0
On comparing with ay2 + by + c = 0,
we get a = 5, b = - 4 and c = 3
Now, D = b2 - 4ac = (-4)2 - 4(5)(3)
= 16 - 60
= - 44 < 0
Since, D < 0, so the given quadratic equation has no real roots.
Q.20. Find the lower limit of median class of the following data if median is 43 : (1 Mark)
Ans. Here, the median is 43 and the corresponding class is 40 - 60. So, median class is 40 - 60.
Lower limit of median class = 40.
Section B
Q.21. What should be added to the polynomial x3 - 3x2 + 6x - 15 so that it is completely divisible by x - 3.
OR
Solve the following pair of linear equations by cross multiplication method : (2 Mark)
x + 2y = 2
x - 3y = 7
Ans.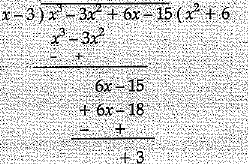
Remainder = 3
Hence, - 3 must be added.
OR
x + 2y - 2 = 0
x - 3y - 7 = 0
Using the formula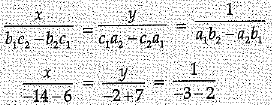
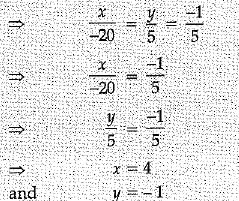
Q.22. Prove that the rectangle circumscribing a circle is a square. (2 Mark)
Ans. Let ABCD be a rectangle
∴ AB = DC and AD = BC ...(i)
We know that length of the tangents drawn from an external point to the circle are of equal lengths.
∴ AP = AS
BP = BQ
CR = CQ
DR = DS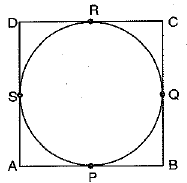
Adding vertically, we have
AB + BP + CR + DR
= AS + BQ + CQ + DS
(AP + BP) + (CR + DR)
= (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = AD + AD [using (i)]
2AB = 2AD
⇒ AB = AD
Since adjacent sides of a rectangle ABCD are equal.
Hence, ABCD is a square.
Q.23. Find the point on F-axis which is equidistant from the points (-5,2) and (9, -2).
Or
If the point P (x, y) is equidistant from the points A(5,1) and B(-1,5), prove that 3x = 2y. (2 Mark)
Ans. Given points are A(-5,2) and 6(9,-2) and let the required point be P(0, y). Then,
PA = PB ⇒ PA2 = PB2
⇒ (0 + 5)2 + (y - 2)2 = (0 - 9)2 + (y + 2)2
⇒ 52 + (y - 2)2 = (- 9)2 + (y + 2)2
⇒ 25 + (y - 2)2 = 81 + (y + 2)2
⇒ (y + 2)2 - (y - 2)2 = (25 - 81)
⇒ 8y = - 56 ⇒ y = - 7.
Hence, the required point is P(0, - 7).
Or
Given the point P(x, y) is equidistant from the points A(5,1)and B(-1,5).
Hence, PA = PB ⇒ PA2 = PB2
⇒ (x - 5)2 + (y - 1)2 = (x + 1)2 + (y - 5)2
⇒ x2 + y2 - 10x - 2y + 26
= x2 + y2 + 2x - 10y + 26
⇒ 12x - 8y = 0 ⇒ 12x = 8y
⇒ 3x = 2y
Q.24. A game consists of tossing a coin 3 times and noting the outcome each time. If getting the same result in all the tosses is a success, find the probability of losing the game.
Or
A box contains 80 discs which are numbered from 1 to 80. If one disc is drawn at random from the box, find the probability that it bears a perfect square number. (2 Mark)
Ans. When a coin is tossed 3 times, all possible outcomes are
Total number of possible outcomes in the sample space = 8, i.e., n(S) = 8
Let A be the event of getting either all three heads or all the three tails.
Then, the favourable outcomes are HHH, TTT.
Number of favourable outcomes for the event A = 2, i,e„ n(A) = 2
Probability of winning the game 
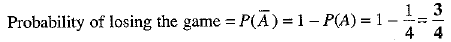
Or
A box contains 80 discs which are numbered from 1 to 80.
Total number of possible outcomes in the sample space = n(S) = 80
Let ‘E’ denote the event that disc drawn from the box is a perfect square number.
E = {1,4, 9, 16, 25,36,49, 64}
∴ n(E) = 8
Probability of getting perfect square number 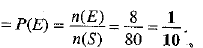
Q.25. If θ be an acute angle and 5 cosec θ = 7, then evaluate sin θ + cos2 θ - 1. (2 Mark)
Ans. Given, 5 cosec θ = 7
or, cosec θ = 7/5
or, 
sin θ + cos2 θ - 1 = sin θ - (1 - cos2 θ)
= sin θ - sin2 θ
(∵ sin2 θ + cos2 θ = 1)
Q.26. Isha is 10 years old girl On the result day Isha and her father Suresh were very happy as she got first position in the. class. While coming back to their home, Isha asked for a treat from her father as a reward for her success. They went to a juice shop and asked for two glasses of juice.
Aisha, a juice seller, was serving juice to her customers in two types of glasses. Both the glasses had inner radius 3 cm. The height of both the glasses was 10 cm.
First type; A glass with hemispherical raised bottom.
Second type : A glass with conical raised bottom of height 1.5 cm. Isha insisted to have the juice in first type of glass and her father decided to have the juice in second type of glass. Out of the two, Isha or her father Suresh, who got more quantity of juice to drink and by how much ? (2 Mark)
Ans. First Type :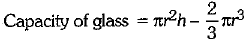
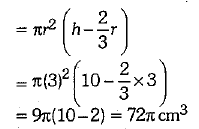
Second Type :
Capacity of glass 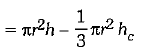
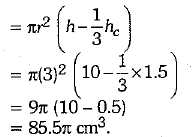
Thus, capacity of second type of glass is more.
Hence, Suresh got more quantity of juice.
Section C
Q.27. Two unbiased coins are tossed simultaneously. Find the probability of getting : (3 Mark)
(i) atleast one head,
(ii) atmost one head,
(iii) no head.
Ans. (i) P (at least pne head) = 3/4
S = {HH, HT, TH, TT} (optional)
(ii) P (at most one head) = 3/4
(iii) P (no head) = 1/4
Q.28. If the sum of first m terms of an AP is the same as the sum of its first n terms, show that the sum of its first (m + n) terms is zero. (3 Mark)
Ans. Let a and d be the first term and common difference respectively.
∴ 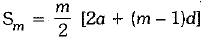
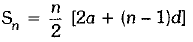
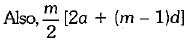
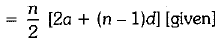
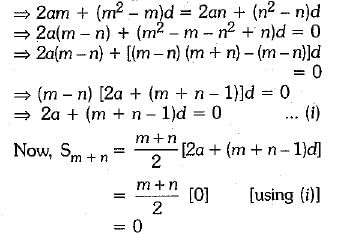
Q.29. A die is thrown once. Find the probability of getting
(i) a even prime number.
(ii) a number divisible by 2.
Or
A card is drawn at random from a well-shuffled pack of 52 cards. Find the probability that the card drawn is neither a red card nor a queen. (3 Mark)
Ans.
There are 6 possible outcomes (1, 2, 3, 4, 5 and 6) in a single throw of a die.
(i) We know that, even prime number is only 2.
So, number of favourable outcomes = 1
∴ P(getting a even prime number) = 1/6.
(ii) The numbers divisible by 2 are 2, 4 and 6.
So,number of favourable outcomes = 3
∴ P (getting a even number divisible by 2)
= 3/6 = 1/2
Number of red cards = 26
Number of queens = 4
But, out of these 4 queens, 2 are red.
∴ Number of queens which are not red = 2
Now, number of cards which are red or queen = 26+2 = 28
∴ P (getting either red card or queen)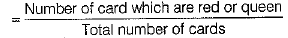
= 28/52 = 7/13
Now, P (not getting either red card or queen)
= 1 - P (getting either red card or queen)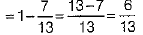
Q.30. Find the point on y-axis which is equidistant from the points (5, - 2) and (- 3, 2).
Or
The line segment joining the points A (2 , 1) and B(5, - 8) is trisected at the points P and Q such that P is nearer to A. If P also lies on the line given by 2x - y + k = 0, find the value of k. (3 Mark)
Ans. The given points are A(5, - 2) and B(- 3, 2).
Let the required point lying on y-axis be P(0, y).
Since point P is equidistant from A and B.
∴ PA = PB
⇒ PA2 = PB2
⇒ (0 - 5)2 + {y - (- 2)}2 = {0 - (- 3)}2 + (y - 2)2
⇒ (- 5)2 + (y + 2)2 = (3)2 + (y - 2)2
⇒ 25 + y2 + 4y + 4 = 9 + y2 - 4y + 4
⇒ 8y = - 16
⇒ y = - 2
Hence, the required point is P(0, - 2)
Or
The given points are A(2, 1) and 5(5, - 8). P and Q are points of trisection such that P is nearer to A. Therefore, point P divides AS internally in the ratio 1 : 2.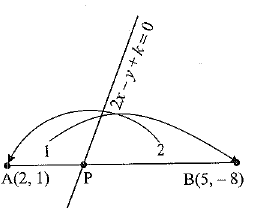
Using section formula, the coordinates of point P are
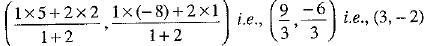
It is given that point 5(3, - 2) lies on the line 2x - y + k = 0
∴ 2 x 3 - (- 2) + k = 0
⇒ 6 + 2 + k = 0
⇒ k = - 8
Q.31. In the figure, PQ is a tangent to a circle with centre O. If ∠OAB = 30°, find ∠ABP and ∠AOB. (3 Mark)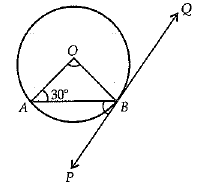
Or
ΔABC is a right angled at C. If p is the length of the perpendicular from C to AB and a, b, c are the lengths of the sides opposite ∠A, ∠B and ∠C respectively, then prove that 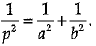
Ans. Since, the tangent is perpendicular to the end point of radius.
Then,
∠OAB = ∠OBA (∵ OA = OB)
∠OBA = 30°
∴ ∠AOB = 180° - (30° + 30°)
∴ ∠ AOB = 120°
∠ABP = ∠OBP - ∠OBA
= 90° - 30° = 60°
Or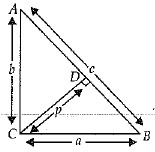
In ΔACB and ΔCDB
∠ACB = ∠CDB = 90°
∠B = ∠B (common)
∴ ΔACB ∼ ΔCDB (by AA Si.milarity)
or, b/p = c/a
or, 1/p = c/ab
Squaring on both sides,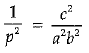
or, 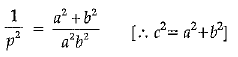
∴ 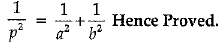
Q.32. If sin θ + cos θ = √3, then prove that tan θ + cot θ = 1.
Or
Evaluate : (3 Mark)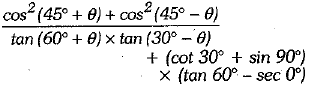
Ans.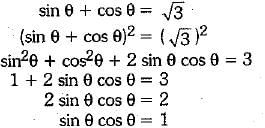

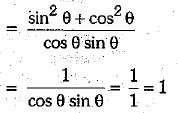
Or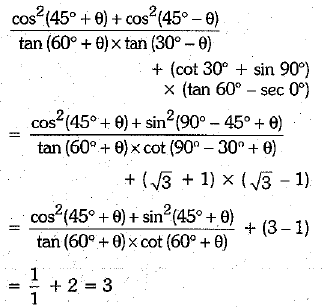
Q.33. If the points P(6,1), Q(8,2), R(9,4), S(P, 3) are the vertices of a parallelogram taken in order, find the value of P.
Or In what ratio does the X-axis divide the line segment joining the points P (-3 , - 2) and Q(1, 4) ? Also find the coordinates of the point of division. (3 Mark)
Ans. Given vertices of the parallelogram are
P(6,1), Q(8,2), R(9, 4) and S(P, 3).
We know that diagonals of a parallelogram bisect each other.
Coordinates of mid-point of diagonal PR = Coordinates of mid-point of diagonal QS.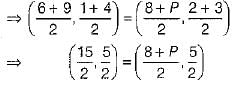
On equating x-coordinates from both sides, we get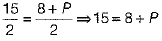
⇒ P = 15 - 8 ⇒ P = 7
Hence the value of P is 7.
Or
Let the line segment joining P(-3, - 2) and Q(1, 4) be divided by the X- axis in the ratio k : 1 at some point A.
PA: AQ = k : 1, then coordinates of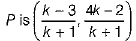
But A lies on the X-axis, therefore its y-coordinate is 0.
⇒ 
⇒ 4k - 2 = 0
⇒ k = 1/2
∴ The ratio is 1:2.
The coordinates of the point of division A is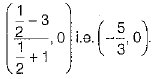
Q.34. Find the area of the shaded region in figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of circle. [Take π = 3.14] (3 Mark)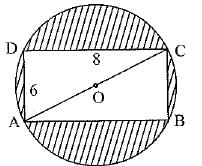
Ans. Length of a rectangle = 8 cm
Breadth of rectangle = 6 cm
∴ The diagonal of a rectangle 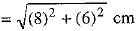
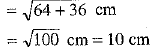
Since the rectangle is inscribed in a circle, therefore the diagonal of a rectangle is the diameter of a circle.
∴ Diameter of a circle = 10 cm
Radius of a circle = 5 cm
From the figure,
Area of the shaded portion
= Area of the circle of radius 5 cm - Area of a rectangle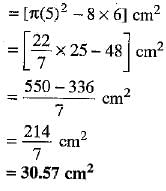
Section D
Q.35. Draw the graphs of the following equations :
2x - y = 1 and x + 2y = 13
Find the solution of the equations from the graph and shade the triangular region formed by the lines and the Y-axis.
OR
The sum of the squares of two consecutive odd numbers is 394. Find the numbers. (4 Mark)
Ans. Given, 2x - y = 1
⇒ y = 2x - 1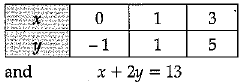
⇒ 

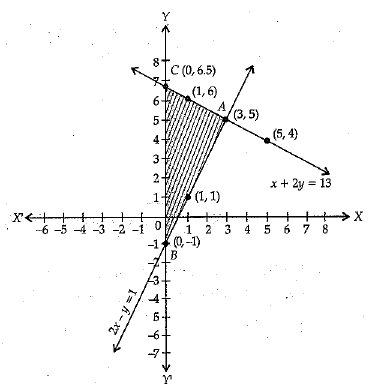
Plotting the above points and drawing the lines joining them, we get the graph of above equations.
Two obtained lines intersect at point A(3,5).
Hence, x = 3 and y - 5.
ABC is the triangular shaded region formed by the obtained lines with the Y-axis.
OR
Let the first odd no. be 2x + 1
∴ Second consecutive odd number = 2x + 1 + 2
= 2x +3
Now, according to question,
(2x + 1)2 + (2x + 3)2 = 394
⇒ 4x2 + 4x + 1 + 4x2 12x + 9 = 394
⇒ 8x2 + 16x - 384 = 0
⇒ x2 + 2x - 48 = 0
⇒ x2 + 8x - 6x - 48 = 0
⇒ x(x + 8) -6(x + 8) = 0
x = - 8 or 6
∴ First number = 2 x 6 + 1
= 13
and second odd number = 15
Q.36. Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio. (4 Mark)
Ans. Given : ΔABC and a line ‘I’ parallel to BC intersects AB at D and AC at E as shown in figure.
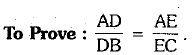
Const.: Join BE and CD.
Draw EL ⊥ AB and DM ⊥ AC.

Since ΔBDE and ΔCDE are triangles on the same base DE and between the same, parallels DE and BC.
∴ Area of ΔBDE = Area of ΔCDE ... (v)
From (iii), (iv) and (v), we have
AD/DB = AE/EC
Q.37. In the given figure, PQL and PRM are tangents to the circle with centre O at the points Q and R, respectively. If S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°, then find the value of ∠QSR. (4 Mark)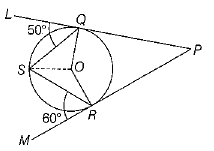
Ans. In the given figure, 0 is the centre of the circle.
Therefore, ∠OQL = ∠ORM = 90°
[∵ radius is perpendicular to the tangent at the point of contact]
Now, ∠OQS = ∠OQL - ∠SQL = 90°-50° = 40°
But ∠OOS = ∠OSQ
[∵ angles opposite to equal sides are equal] ∠OSQ = 40°
Similarly, ∠OSR = ∠ORS = ∠ORM - ∠SRM
= 90°-60° = 30°
Now, ∠QSR = ∠OSQ + ∠OSR = 40° + 30° = 70°
Q.38. A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308,8 cm3. The radii of the top and bottom of circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of metal sheet used in making it. [Use π = 3.14] (4 Mark)
Ans. Let r = 12 cm and R = 20 cm be the radii of the bottom and top circular ends of a open bucket.
Then, volume of the bucket, i.e., capacity of a bucket.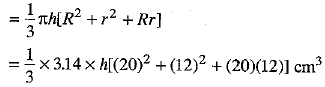

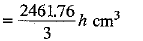 .......(1)
.......(1)
It is given that the capacity of a open bucket
= 12308.8 cm3 .......(2)
From (1) and (2), we have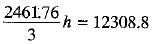
⇒ 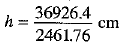
⇒ h = 15 cm
Slant height of a open bucket (l)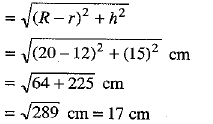
Total area of metal sheet used in the bucket
Q.39. A round thali has 2 inbuilt triangular for serving vegetables and a separate semi-circular area for keeping rice or chapati. If radius of thali is 21 cm, find the area of the thali that is shaded in the figure. (4 Mark)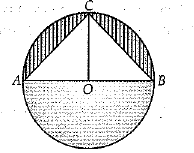
Or
A toy is in the form of a cylinder of diameter  and height 3.5 m surmounted by a cone whose vertical angle is 90°. Find total surface area of the toy.
and height 3.5 m surmounted by a cone whose vertical angle is 90°. Find total surface area of the toy.
Ans. Since, AOB is the diameter of the circle. So, Area Of shaded region = (Area of semi-circle - Area of ΔABC)
Area of semi-circle =1386/2 = 693 cm2
= 1386/2 = 693 cm2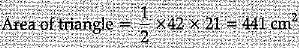
Area of shaded region = 693 - 441
= 252 sq cm
Or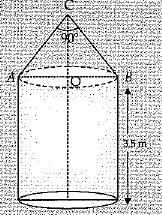
Since ∠ C = 90º
AC = BC = x(say)
AB2 = AC2 + BC2
AB2 = x2 + x2
2x2 = (2√2)2
or, x = 2 and r = 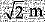
∴ Slant height of conical portion = 2 m
Total surface area of toy = 2πrh πr2 + πrl
Q.40. Daily wages of 110 workers, obtained in a survey, are tabulated below :
Compute the mean daily wages and modal daily wages of these workers. (4 Mark)
Ans.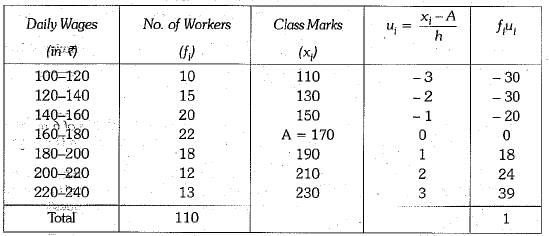
Let assumed mean (A) = 170
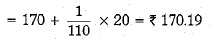
Modal class is 160-180
∴l = 160, h = 20, f1 = 22, f0 = 20, f2 = 18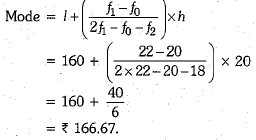
|
303 docs|7 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 6 - CBSE Sample Papers For Class 10
| 1. What is the format of the CBSE Sample Question Paper for Class 10 Mathematics (2019-20)? |  |
| 2. How can I prepare for the Class 10 Mathematics exam using the CBSE Sample Question Paper? |  |
| 3. Are the questions in the CBSE Sample Question Paper similar to the actual board exam? |  |
| 4. Can I rely solely on the CBSE Sample Question Paper for my Class 10 Mathematics exam preparation? |  |
| 5. How can I access the CBSE Sample Question Paper for Class 10 Mathematics (2019-20)? |  |

|
Explore Courses for Class 10 exam
|

|

















