Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Standard) - 4 | CBSE Sample Papers For Class 10 PDF Download
Class X
Mathematics – Standard
Sample Question Paper 2020-21
Max. Marks : 80
Duration : 3 hrs.
General Instructions :
1. This question paper contains two parts A and B.
2. Both Part A and Part B have internal choices.
Part – A :
1. It consists two sections - I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part – B :
1. Section III, Question No. 21 to 26 are Very short answer Type questions of 2 marks each.
2. Section IV, Question No. 27 to 33 are Short Answer Type questions of 3 marks each.
3. Section V, Question No. 34 to 36 are Long Answer Type questions of 5 marks each.
4. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Sections - I
Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
Q.1. Find the LCM of smallest two digit composite number and smallest single digit composite number. (1 Mark)
OR
The decimal representation of 11 / 23 x 5 will terminate after how many places? (1 Mark)
Ans. Since, the smallest composite number = 4
The smallest 2 digit composite number = 10
∴ LCM of 4 and 10.
4 = 2 × 2
10 = 5 × 2
L.C.M. = 2 × 5 × 2
= 20
∴ LCM of 4 and 10 = 20
OR
Since 11 / 23 x 5 = 11 x 52 / 23 x 53
= 275 / 103 = 0.275
Thus, 11 / 23 x 5 will terminate after 3 decimal places.
Q.2. If the zeroes of the quadratic polynomial ax2 + bx + c, a ≠ 0 are equal, then what are the signs of a and c? (1 Mark)
OR
Show that the sum of roots of quadratic equation –x2 + 3x – 3 = 0 is 3. (1 Mark)
Ans. For equal roots b2 – 4ac = 0 or b2 = 4ac b2 is always positive so 4ac must be positive, i.e., product of a and c must be positive, i.e., a and c must have same sign either positive or negative.
OR
–x2 + 3x – 3 = 0
On comparing with
ax2 + bx + c = 0 a = – 1, b= 3, c = – 3
∴ Sum of the roots = -b / a = -3 / -1 = 3
Q.3. The point which divides the line segment joining the points (8, – 9) and (2, 3) in ratio 1 : 2 internally lies in which quadrant? (1 Mark)
OR
If HCF of 14 and 180 is expressed in the form 13m – 16. Find the value of m. (1 Mark)
Ans. 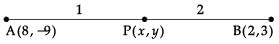
m = 1, n = 2
Given, (x1, y1) = (8, – 9)
(x2, y2) = (2, 3)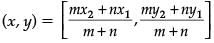
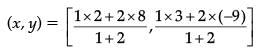
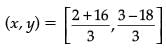
(x, y) = [18 / 3, -15 / 3]
(x, y) = (6, – 5)
Hence, the point (6, – 5) lies in IV quadrant.
OR
Given, HCF of 144 and 180 is in form of 13m – 16,
Now, HCF of 144 and 180.
144 = 2 × 2 × 2 × 2 × 3 × 3
180 = 2 × 2 × 3 × 3 × 5
∴ HCF (144, 180) = 2 × 2 × 3 × 3
= 36
∵ HCF of 144 and 180 is given in the form of 13m - 16,
∴ 13m - 16 = 36
13m = 36 + 16
13m = 52
m = 52 / 13
m = 4
Q.4. If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then DE / PQ = FE / RP is true? Justify (1 Mark)
Ans. In D DEF and DPQR, ∠D = ∠Q and ∠R = ∠E. By AA similarity, we get DDEF ~ DQRP.
Hence, DE / QR = EF / RP = DF / QP.
Q.5. At one end A of diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. Find the length of the chord CD which is at a distance 8 cm from A and parallel to XY. (1 Mark)
Ans. XAY is tangent and AO is radius at contact point A of circle.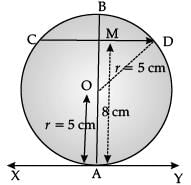 AO = 5 cm
AO = 5 cm
∴ ∠OAY = 90°
CD is another chord at distance (perpendicular) of 8 cm from A and CMD || XAY meets AB at M.
Join OD.
OD = 5 cm
OM = 8 – 5 = 3 cm
∠OMD = ∠OAY = 90°
Now, in right angled ΔOMD
MD2 = OD2 – MO2
= 52 – 32
= 25 – 9
= 16
⇒ MD = 4 cm
We know that, Perpendiculars from centre O of circle bisect the chord.
∴ CD = 2
= 2 × 4
= 8 cm.
Hence, length of chord, CD = 8 cm.
Q.6. Find the area of a sector of angle p (in degrees) of a circle with radius R. (1 Mark)
Ans. We know that area of sector of angle θ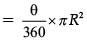
Area of sector of angle, p =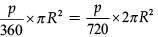
Q.7. Find HCF of the number k, 2k, 3k, 4k and 5k, where k is a positive integer. (1 Mark)
Ans. HCF of
Q.8. The probability expressed as a percentage of a particular occurrence can never be less than 0. Is the above statement is true of false, justify. (1 Mark)
Ans. Probability lies between 0 and 1 and when it is converted into percentage it will be between 0 and 100. So, cannot be negative.
Q.9. Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, then find the equation of a second line. (1 Mark)
Ans. The equation of one line is 4x + 3y = 14. We know that if two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are parallel, then
a1 / a2 = b1 / b2 ≠ c1 / c2
or 4 / a2 = 3 / b2 ≠ -14 / c2 ⇒ a2 / b2 = 4 / 3 ⇒ 12 / 9
Hence, one of the possible, second parallel line is 12x + 9y = 5.
Q.10. If 7 times the 7th term of an A.P. is equal to 11 times its 11th term, then find it's 18th term. (1 Mark)
Ans. According to question,
7t7 = 11t11
7 (a + 6d) = 11 (a + 10d)
4a + 68d = 0
4 (a + 17d) = 0
a + 17d = 0
t18 = 0.
Q.11. Find the ratio in which the line segment joining the points (6, 4) and (1, – 7) is divided by the x-axis. (1 Mark)
OR
Find the coordinates of a point A, where AB is diameter of a circle whose centre is (2, –3) and B is the point (1, 4). (1 Mark)
Ans. Let the line segment joining the given points is divided by the x-axis in the ratio k : 1 at point P.
∴ The coordinates of P are (k + 6 / k + 1, -7k + 4 / k + 1)
Since, y coordinates of every point on the x-axis is zero. -7k + 4 / k + 1 = 0 ⇒ – 7k + 4 = 0
⇒ k = 4 / 7
So, required ratio is 4 : 7.
OR
Since, AB is the diameter, centre C must be the mid point of the diameter of AB.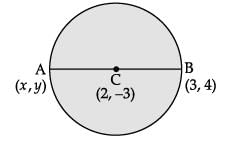 Let the co-ordinates of point A be (x, y). x-coordinate of C = x + 1 / 2
Let the co-ordinates of point A be (x, y). x-coordinate of C = x + 1 / 2
⇒ 2 = x + 1 / 2
⇒ 4 = x + 1
⇒ x = 3
and y-coordinate of C = y + 4 / 2
⇒ - 3 = y + 4 / 2
⇒ –6 = y + 4
⇒ y = –10
Hence, coordinates of point A is (3, –10).
Q.12. If the angle between two tangent drawn from an external point 'p' to a circle of radius 'r' and centre O is 60°, then find the length of OP. (1 Mark)
OR
In the figure, QR is a common tangent to a given circle which meet at T. Tangent at T meets QR at P. If QP = 3.8 cm, then find length of QR. (1 Mark) Ans.
Ans. 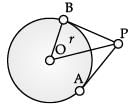
In ΔOBP, OB / OP = sin 30°
∴ OP = 2r
OR
QP = 3.8
QP = PT
(Length of tangents from external points are equal)
or, PT = 3.8 cm
PR = PT = 3.8 cm
or, QR = QP + PR
= 3·8 + 3·8 = 7.6 cm.
Q.13. If k + 1 = sec2θ (1 + sinθ) (1 – sinθ), then find the value of k. (1 Mark)
Ans. k + 1= sec2θ (1 + sinθ) (1 – sinθ)
or, k + 1 = sec2θ (1 – sin2θ)
or, k + 1 = sec2θ.cos2θ[∵ sin2θ + cos2θ = 1]
or, k + 1 =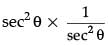
or, k + 1 = 1
or, k = 1 – 1
∴ k = 0.
Q.14. A cylinder, a cone and a hemisphere have same base and same height. Find the ratio of their volumes. (1 Mark)
Ans. Volume of cylinder : Volume of cone : Volume of hemisphere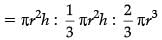
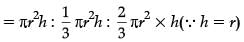
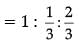
or, 3 : 1 : 2
Q.15. A steel wire when bent in the form of a square encloses an area of 121 cm2. If the same wire is bent in the form of a circle, then find the circumference of the circle. (1 Mark)
Ans. Area of square = (side)2 = 121 cm2
Side of square = √121 = 11 cm
Perimeter of square = 4 × 11 = 44 cm.
Circumference of the circle = Perimeter of the square
= 44 cm
Q.16. Following distribution gives cumulative frequencies of 'more than type' : (1 Mark)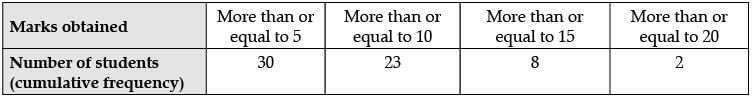
Change the above data to a continuous grouped frequency distribution.
Ans. 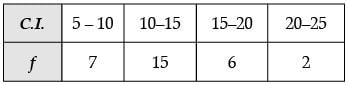
Section - II
Case study based questions are compulsory. Attempt any four sub parts of each question. Each subpart carries 1 mark
Q.17. Case Study based - 1 :
Small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of 1 / 4 m and a tread of 1 / 2 m (see figure below).
Each step has a rise of 1 / 4 m and a tread of 1 / 2 m (see figure below).
(a) What is the volume of the required concrete for step 1? (1 Mark)
(i) 25 / 4
(ii) 50 / 4
(iii) 75 / 4
(iv) 150 / 4
Ans. (i)
Solution. For the 1st step, the volume of required concrete is
1 / 4 x 1 / 2 x 50 = 25 / 4
(b) What is the volume of the required concrete for step 2? (1 Mark)
(i) 25 / 4
(ii) 50 / 4
(iii) 75 / 4
(iv) 150 / 4
Ans. (ii)
Solution. For the 2nd step, the volume of required concrete is
2 / 4 x 1 / 2 x 50 = 50 / 4
(c) What is the volume of the required concrete for step 3? (1 Mark)
(i) 25 / 4
(ii) 50 / 4
(iii) 75 / 4
(iv) 150 / 4
Ans. (i)
Solution. For the 3rd step, the volume of required concrete is
3 / 4 x 1 / 2 x 50 = 75 / 4
(d) The given problem is based on which mathematical concept? (1 Mark)
(i) AP
(ii) Surface areas and volumes
(iii) Height and Distances
(iv) None of these
Ans. (i)
Solution. The numbers involved in this case in AP in which
a = 25 / 4, d = 25 / 4, n = 15
(e) What is the total volume of concrete to build the terrace? (1 Mark)
(i) 750 m3
(ii) 500 m3
(iii) 570 m3
(iv) 1000 m3
Ans. (i)
Solution. Since,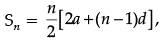 we have
we have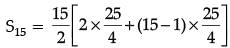
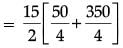
= 15 / 2 x 400 / 4
= 750
Thus, the total volume of concrete required to build the terrace is 750 m3.
Q.18. Case Study based - 2 :
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in Figure. Niharika runs 1/4th the distance AD on the second line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag.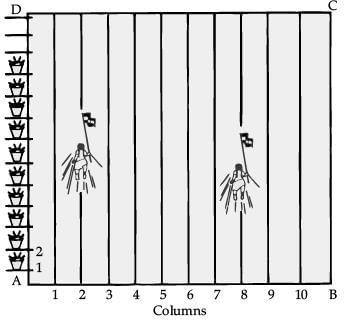
(a) At what distance Niharika posted the green flag from the starting point of second line? (1 Mark)
(i) 20 m
(ii) 25 m
(iii) 100 m
(iv) 50 m
Ans. (ii)
Solution. It can be observed that Niharika posted the green flag at one-fourth of the distance AD, i.e., (1 × 100 / 4) m = 25 m from the starting point of second line.
(b) At what distance Preet posted the green flag from the starting point of eighth line? (1 Mark)
(i) 20 m
(ii) 25 m
(iii) 100 m
(iv) 50 m
Ans. (i)
Solution. Preet posted the red flag at one-fifth of the distance AD, i.e., (1 × 100 / 5) m = 20 m from the starting point of eighth line.
(c) What is the distance between both the flags? (1 Mark)
(i) √61 m
(ii) √101 m
(iii) √51 m
(iv) √11 m
Ans. (i)
Solution. Position of Niharika's flag is at (2, 25) and position of Preet's flag is at (8, 20). Distance between these flags by using Distance.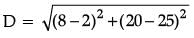
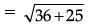
= √61 m
(d) If Rashmi has to post a blue flag exactly halfway between the line segments joining the two flags, where should she post her flag? (1 Mark)
(i) (5, 22.5)
(ii) (22.5, 5)
(iii) (5, 5)
(iv) None of these
Ans. (i)
Solution. The point at which Rashmi should post her blue flag is the mid-point of the line joining these points. Let this point be A(x, y).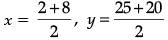
x = 10 / 2 = 5 y = 45 / 2 = 22.5
Hence, A(x, y) = (5, 22.5)
Therefore, Rashmi should post her blue flag at 22.5 m on fifth line.
(e) The given problem is based on which mathematical concept? (1 Mark)
(i) Lines
(ii) surface areas and volumes
(iii) Triangles
(iv) None of these
Ans. (ii)
Q.19. Case Study based - 3 :
A carpenter made a wooden pen stand. It is in the shape of cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. (See Figure).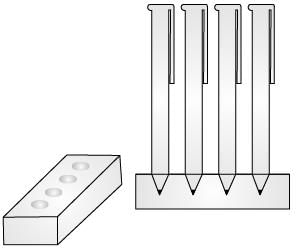
(a) What is the volume of cuboid? (1 Mark)
(i) 525 cm3
(ii) 225 cm3
(iii) 552 cm3
(iv) 255 cm3
Ans. (i)
Solution. For cuboid
l = 15 cm, b = 10 cm and h = 3.5 cm
Volume of the cuboid = l × b × h
= 15 × 10 × 3.5
= 525 cm3
(b) What is the volume of cone? (1 Mark)
(i) 11 / 3cm3
(ii) 11 / 30cm3
(iii) 3 / 11cm3
(iv) 30 / 11cm3
Ans. (ii)
Solution. For cone :
r = 0.5 cm, h = 1.4 cm
Volume of four conical depressions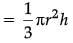
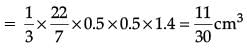
(c) What is the total volume of conical depressions? (1 Mark)
(i) 1.74 cm3
(ii) 1.44 cm3
(iii) 1.47 cm3
(iv) 1.77 cm3
Ans. (iii)
Solution. Volume of four conical depressions = 4 x 11 / 30 = 1.47 cm3
(d) What is the volume of wood in the entire stand? (1 Mark)
(i) 522.35 cm3
(ii) 532.53 cm3
(iii) 523.35 cm3
(iv) 523.53 cm3
Ans. (iv)
Solution. Volume of the wood in the entire stand
= Volume of cuboid – Volume of 4 conical depression
= 525 – 1.47
= 523.53 cm3
(e) The given problem is based on which mathematical concept? (1 Mark)
(i) Triangle
(ii) Lines
(iii) Height and Distances
(iv) None of these
Ans. (ii)
Q.20. Case Study based - 4 :
The maximum bowling speeds, in km per hour, of 33 players at a cricket coaching centre are given as follows.
(a) What is the modal class of the given data? (1 Mark)
(i) 85 - 100
(ii) 100 - 115
(iii) 115 - 130
(iv) 130 - 145
Ans. (i)
Solution. Modal class is the class with highest frequency i.e., 85 – 100
(b) What is the value of class interval for the given data set? (1 Mark)
(i) 10
(ii) 15
(iii) 5
(iv) 20
Ans. (ii)
Solution. Class interval = 100 – 85 = 15
= 115 – 100
= 130 – 115 = 145 – 130
(c) What is the median class of the given data? (1 Mark)
(i) 85 - 100
(ii) 100 - 115
(iii) 115 - 130
(iv) 130 - 145
Ans. (ii)
Solution. N = Number of observations = 33 (odd)
Median of 33 observations = 17th observation, which lies in class 100 – 115
(d) What is the median blowing speed? (1 Mark)
(i) 109.17 km/hr
(ii) 109.71 km/hr
(iii) 107.17 km/hr
(iv) 109.19 km/hr
Ans. (i)
Solution.
Median =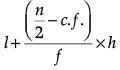
l = 100, f = 9, c.f. = 11, h = 100 – 85 = 15
Median =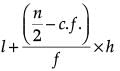
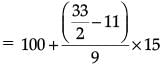
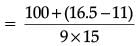
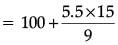
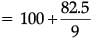
= 100 + 9.166
= 109.17 km/h
Hence, the median bowling speed is 109.17 km/h
(e) What is the sum of lower limit of modal class and upper limit of median class? (1 Mark)
(i) 100
(ii) 200
(iii) 300
(iv) 400
Ans. (ii)
Solution. lower limit of modal class = 85
and upper limit of median class = 115
sum = 85 + 115 = 200
Part - B
Section - III
All questions are compulsory. In case of internal choices, attempt any one.
Q.21. Given that √5 is irrational, prove that 2√5 - 3 is an irrational number. (2 Mark)
Ans. Let us assume, to the contrary, that 2√5 − 3 is a rational number
∴ 2√5 − 3 = p / q , where p and q are integers and q ≠ 0
⇒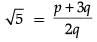 .....(1)
.....(1)
Since p and q are integers
∴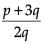 is a rational number
is a rational number
∴ √5 is a rational number which is contradiction as √5 is an irrational number
Hence our assumption is wrong and hence 2√5 − 3 is an irrational number.
Q.22. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes. (2 Mark)
Ans. 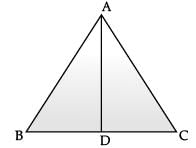 AD ⊥ BC ∴ In ΔABD, AB2 = AD2 + BD2
AD ⊥ BC ∴ In ΔABD, AB2 = AD2 + BD2
⇒ AB2 = AD2 + BC2 / 4 or 4AB2 = 4AD2 + BC2
⇒ 3AB2 = 4AD2
Q.23. Find the value of : sin 30°. cos 60° + cos 30°. sin 60° Is it equal to sin 90° or cos 90°? (2 Mark)
OR
Prove that :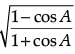 = cosec A – cot A (2 Mark)
= cosec A – cot A (2 Mark)
Ans. sin 30° cos 60° + cos 30° sin 60°
= 1 / 2 x 1 / 2 + √3 / 2 x √3 / 2
= 1 / 4 + 3 / 4
= 4 / 4 = 1
It is equal to sin 90° = 1 but not equal to cos 90° as cos 90° = 0.
OR
LHS =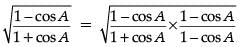
=
=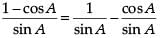
= cosec A – cot A = RHS
Hence proved.
Q.24. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. (2 Mark)
Ans. 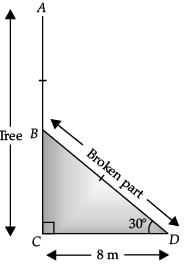
Let the tree be AC and is broken at B. The broken part touches at the point D on the ground.
In right angled ΔBCD,
cos 30° = CD / BD
⇒ √3 / 2 = 8 / BD
⇒ BD = 16 / √3
and tan 30° = BC / CD
⇒ 1 / √3 = BC / 8
⇒ BC = 8 / √3
∴ Height of tree= BC + BD
= 8 / √3 + 16 / √3
=
=
=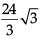
Hence, the height of the tree = 8√3 m.
Q.25. A paper is in the form of a rectangle ABCD in which AB = 20 cm and BC = 14 cm. A semi-circular portion with BC as diameter is cut off. Find the area of the remaining part. (Use π = 22 / 7) (2 Mark)
OR
If the perimeter of a protractor is 72 cm, calculate its area. (Use π = 22 / 7) (2 Mark)
Ans. Area of remaining part = Area of rectangle – Area of semi-circle
=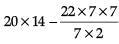
= 280 – 77
Hence, area of remaining part = 203 cm2.
OR
Perimeter of semi-circle,
(π + 2)r = 72 cm
or,
or,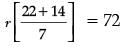
or, 36 / 7 r = 72
r = 14 cm
∴ Area of protractor =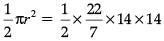
= 308 cm2.
Q.26. Find the mean of first five odd multiples of 5. (2 Mark)
Ans. The first five odd multiples of 5, according to the problem are : 5, 15, 25, 35 and 45
Mean =
= 125 / 5 = 25
Section - IV
All questions are compulsory. In case of internal choices, attempt any one.
Q.27. Find the zeroes of the following polynomial : 5√5x2 + 30x+ 8√5 (3 Mark)
OR
Find the zeroes of the quadratic polynomial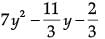 and verify the relationship between the zeroes and the coefficients. (3 Mark)
and verify the relationship between the zeroes and the coefficients. (3 Mark)
Ans. 5√5x2 + 30x + 8√5
= 5√5x2 + 20x + 10x + 8√5
= 5x(√5x + 4) + 2√5 (√5x + 4)
= (√5x + 4)( 5x + 2√5)
Thus, zeroes are -4 / √5 = -4√5 / 5 and -2√5 / 5
OR
p(y) =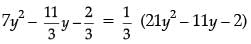
=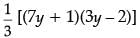
∴ Zeroes are 2 / 3, -1 / 7
Sum of zeroes = 2 / 3 - 1 / 7 = 11 / 21
-b / a = 11 / 21 ∴ sum of zeroes = -b / a
Product of zeroes = (2 / 3)(-1 / 7) = -2 / 21
c / a = -2 / 3(1 / 7) = -2 / 21 ∴ Product = c / a
Detailed Solution :
Given, polynomial is ...(i)
...(i)
⇒ 21y2 – 11y – 2 = 0
⇒ 21y2 – 14y + 3y – 2 = 0
⇒ 7y (3y – 2) +1 (3y – 2) = 0
⇒ (3y – 2)(7y + 1) = 0
⇒ y = 2 / 3 or y = -1 / 7
Hence, zeros of given polynomial are
y = 2 / 3 and y = -1 / 7
On comparing eq(i) with ax2 + bx + c = 0, we get
a = 21, b = –11 and c = –2
Now, Sum of roots = 2 / 3 + (-1 / 7)
= 2 / 3 - 1 / 7
= 14 - 3 / 7
= 11 / 21
= -b / a
Hence verified
and Product of roots = 2 / 3 x (-1 / 7)
= -2 / 21
= c / a
Hence verified.
Q.28. Represent the following pair of linear equations graphically and hence comment on the condition of consistency of this pair. x – 5y = 6, 2x – 10y = 12. (3 Mark)
OR
In the figure, ABCDE is a pentagon with BE || CD and BC || DE. BC is perpendicular to CD. AB = 5 cm, BE = 7 cm, BC = x – y and CD = x + y. If the perimeter of ABCDE is 27 cm. find the value of x and y, given x, y ≠ 0. (3 Mark)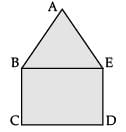 Ans. Given, x – 5y = 6 ⇒ y = x - 6 / 5
Ans. Given, x – 5y = 6 ⇒ y = x - 6 / 5
and 2x – 10y = 12 ⇒ y = x - 6 / 5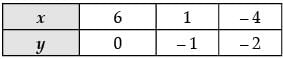
 Since, the lines are coincident, so the system of linear equations is consistent with infinitely many solutions.
Since, the lines are coincident, so the system of linear equations is consistent with infinitely many solutions.
OR
x + y = 7 and 2 (x – y) + x + y + 5 + 5 = 27
∴ x + y = 7 and 3x – y = 17
Solving, we get, x = 6 and y = 1
Q.29. ad ≠ bc, then prove that the equation. (a2 + b2)x2 + 2(ac + bd)x + (c2 + d2) = 0 has no real roots. (3 Mark)
Ans. We have, A = (a2 + b2), B = 2(ac + bd) and C = (c2 + d2)
For no real roots, D < 0
i.e., D ⇒ b2 – 4ac < 0
b2 – 4ac = [2(ac + bd)]2 – 4(a2 + b2)(c2 + d2)]
= 4[a2c2 + 2abcd + b2d2] – 4[a2c2 + a2d2 + b2c2 + b2d2]
= 4[a2c2 + 2abcd + b2d2 – a2c2 – a2d2 – b2c2 – b2d2]
= – 4[a2d2 + b2c2 – 2abcd]
= – 4(ad – bc)2
Since, ad ≠ bc
Therefore, D < 0
Hence, the equation has no real roots.
Q.30. If the sum of the first 14 terms of an A.P. is 1050 and its first term is 10, find its 20th term. (3 Mark)
Ans. Given, a = 10, and S14 = 1050
Let the common difference of the A.P. be d.
Since,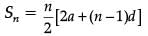
∴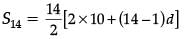
= 1050
20 + 13d = 1050 / 7 = 150
13d = 130
d = 130 / 13 = 10
an = a + (n – 1)d
a20 = 10 + 19 × 10 = 200
Hence, a20 = 200.
Q.31. In Figure PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting PQ at A and RS at B. Prove that ∠AOB = 90°. (3 Mark)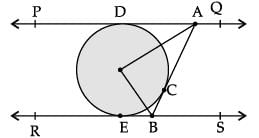 Ans. ΔAOD ≌ ΔAOC [SAS]
Ans. ΔAOD ≌ ΔAOC [SAS]
⇒ ∠1 = ∠2
Similarly ∠4 = ∠3
⇒ ∠1 + ∠4 = ∠2 + ∠3 = 1 / 2 (180°)
⇒ ∠2 + ∠3 = 90° or ∠AOB = 90° Detailed Solution :
Detailed Solution :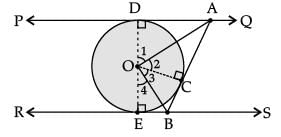 In ΔDOA and ΔCOA
In ΔDOA and ΔCOA
DA = AC
[Tangents drawn from common point]
∠ODA = ∠OCA = 90°
[angle between tangent and radius]
OD = OC ( radius of circle)
∴ ΔDOA ≅ ΔCOA (By SAS)
Hence, ∠1 = ∠2 i.e., ∠DOA = ∠COA (By cpct) ...(i)
Similarly, ΔBOC ≅ ΔBOE (By SAS)
∴ ∠3 = ∠4 i.e., ∠COB = ∠BOE (By cpct.) ...(ii)
Now, ∠1+ ∠2 + ∠3 + ∠4 = 180° (angles on a straight line)
2∠2 + 2 ∠3 = 180°
[from eq(i) & eq(ii)] ∠2 + ∠3 = 90°
i.e., ∠AOC + ∠BOC = 90° or ∠AOB = 90°
Hence Proved.
Q.32. sinθ + cosθ = √3 , then prove that tanθ + cotθ = 1 (3 Mark)
Ans. sinθ + cosθ = √3 ⇒ (sinθ + cosθ)2 = 3
⇒ 1 + 2sinθ cosθ = 3 ⇒ sinθ cosθ = 1
∴ tanθ + cotθ = sinθ / cosθ + cosθ / sinθ = 1
Detailed Solution :
Given sinθ + cosθ = √3
Squaring on both sides,
(sinθ + cosθ)2 = (√3)2
sin2θ + cos2θ + 2sinθ cosθ = 3
1 + 2sinθ cosθ = 3
2sinθ cosθ = 2
sinθ cosθ = 1 ... (i)
∴ tanθ + cotθ = sinθ / cosθ + cosθ / sinθ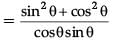
Now using equation (i) =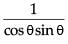
= 1 / 1 = 1
Q.33. A box consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Ramesh, a shopkeeper will buy only those shirts which are good but ‘Kewal’ another shopkeeper will not buy shirts with major defects. A shirt is taken out of the box at random.
What is the probability that : (3 Mark)
(i) Ramesh will buy the selected shirt?
(ii) ‘Kewal ‘ will buy the selected shirt?
Ans. (i) Number of good shirts = 88
P (Ramesh buys the shirt) = 88 / 100 or 22 / 25
(ii) Number of shirts without major defect = 96
P (Kewal buys a shirt) = 96 / 100 or 24 / 25
Section - V
All questions are compulsory. In case of internal choices, attempt any one.
Q.34. Amit, standing on a horizontal plane, find a bird flying at a distance of 200 m from him at an elevation of 30°. Deepak standing on the roof of a 50 m high building, find the angle of elevation of the same bird to be 45°. Amit and Deepak are on opposite sides of the bird. Find the distance of the bird from Deepak. (5 Mark)
OR
The angle of depression of two ships from an aeroplane flying at the height of 7500 m are 30° and 45°. If both the ships are in the same line that one ship is exactly behind the other, find the side such distance between the ships. (5 Mark)
Ans. 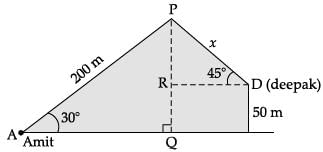 In ΔAPQ
In ΔAPQ
PQ / AP = sin 30° = 1 / 2
PQ = (200) (1 / 2) = 100 m
PQ = 100 – 50 = 50 m
In ΔPRD, PR / PD = sin 45° = 1 / √2
PD = (PR) (√2)
= 50√2 m
Detailed Solution :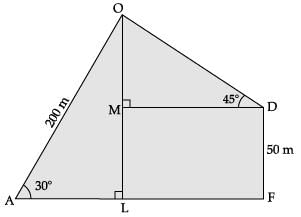
Let O be the position of the bird, A be the position for Amit, D be the position for Deepak and FD be the building at which Deepak is standing at height 50m.
Given, AO = 200m and FD = 50m
In ΔOLA, ∠L = 90°
sin 30° = OL / OA
⇒ 1 / 2 = OL / 200
⇒ OL = 200 / 2
= 100m
∴ OM = OL – LM
= OL – FD
= (100 – 50)m = 50m
In ΔOMD, ∠M = 90°
sin 45° = OM / OD
⇒ 1 / √2 = 50 / OD
⇒ OD = 50√2
= 50 × 1.414
= 70.7m
Thus, the distance of the bird from Deepak is 70.7 m.
OR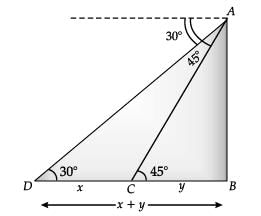 In ΔABC, AB / BC = tan 45°
In ΔABC, AB / BC = tan 45°
⇒ 7500 / y = 1
⇒ y = 7500
In ΔABD, AB / BD = tan 30°
7500 / x + y = 1 / √3
⇒ x + y = 7500√3
x + 7500 = 7500√3
x = 7500√3 − 7500
= 7500 (√3 −1)
= 7500(1·73 – 1)
= 7500 × 0·73
= 5475 m
Hence, the distance between two ships
= 5475 m
Q.35. A hemispherical portion is cut from one face of a cubical block, such that diameter ‘l’ of hemisphere is equal to the edge of cube. Find the surface area of the remaining solid. (5 Mark)
Ans. Let the radius of hemisphere = r
∴ Therefore, r = l / 2
Now, the required surface area = Surface area of cubical block – Area of base of hemisphere + Curved surface area of hemisphere.
= 6(side)2 – πr2 + 2πr2
=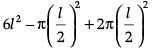
=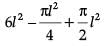
=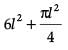
Required surface area =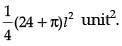
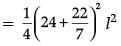
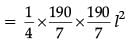
= 184.18 l2 unit2
Q.36. Given, Solve for x :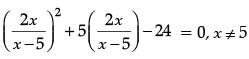 (5 Mark)
(5 Mark)
Ans. Given,
Let 2x / (x - 5) = y
∴ y2 + 5y – 24 = 0
⇒ (y + 8) (y – 3) = 0
y = 3 or – 8
Putting y = 3 we get
2x / x - 5 = 3
2x = 3x – 15
⇒ x = 15
Again, for y = – 8, 2x / x - 5 = -8
2x = – 8x + 40
10x = 40
x = 4
Hence, x = 15 or 4
|
303 docs|7 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Standard) - 4 - CBSE Sample Papers For Class 10
| 1. What is the importance of solving CBSE sample question papers for Class 10 Mathematics? |  |
| 2. How can solving CBSE sample question papers help in improving time management during the Class 10 Mathematics exam? |  |
| 3. Are the CBSE sample question papers for Class 10 Mathematics available online? |  |
| 4. Can solving CBSE sample question papers increase the chances of scoring higher marks in the Class 10 Mathematics exam? |  |
| 5. How can students effectively utilize CBSE sample question papers for Class 10 Mathematics for self-assessment? |  |

|
Explore Courses for Class 10 exam
|

|

















