Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Standard) - 3 | Mathematics (Maths) Class 10 PDF Download
Class X
Mathematics – Standard
Sample Question Paper 2020-21
Max. Marks : 80
Duration : 3 hrs.
General Instructions :
1. This question paper contains two parts A and B.
2. Both Part A and Part B have internal choices.
Part – A :
1. It consists two sections - I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part – B :
1. Section III, Question No. 21 to 26 are Very short answer Type questions of 2 marks each.
2. Section IV, Question No. 27 to 33 are Short Answer Type questions of 3 marks each.
3. Section V, Question No. 34 to 36 are Long Answer Type questions of 5 marks each.
4. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Sections - I
Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
Q.1. What is the product of a non-zero rational and an irrational number? (1 Mark)
OR
If two positive integers a and b are written as a = x3y2 and b = xy3; where x, y are prime numbers, then HCF of a and b. (1 Mark)
Ans. The product of a non-zero rational with and an irrational number is always irrational.
OR
Since a = x3y2 = x x x x x x y x y and
b = xy3 = x x y x y x y,
Thus, HCF of a and b = x x y x y = xy2
Q.2. If one of the zeroes of the cubic polynomial x3 + ax2 + bx + c is −1, then the product of the other two zeroes. (1 Mark)
OR
Is equation x2 + x – 5 = 0 has two distinct real roots ? Justify (1 Mark)
Ans. Let f( x) = x3 + ax2 + bx + c
∵ One of the zeroes of f(x) is –1 so
f (-1) = 0
(-1)3 + a(-1)2 + b(-1) + c = 0
-1 + a - b + c = 0
a - b + c = 1
c = 1 + b - a
Now, αβγ = -d / a [∵ a = 1, d = c]
-1βγ = -c / 1
βγ = c
βγ = 1 + b – a
OR
x2 + x – 5 = 0
On comparing with ax2 + bx + c = 0
a = 1, b = 1, c = – 5
Discriminant D = b2 – 4ac = 0
(1)2 – 4 (1) (– 5) = 1 + 20 = 21 > 0
Hence, the equation has two distinct real roots.
Q.3. AOBC is a rectangle whose three vertices are vertices A (0, 3), O (0, 0) and B (5, 0). What is the length of the diagonal? (1 Mark)
OR
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR. (1 Mark)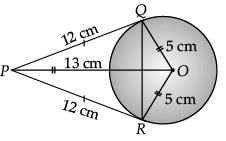 Ans. According to the question, a triangle can be represented as :
Ans. According to the question, a triangle can be represented as :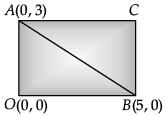 ∴ Distance between the points A (0, 3) and B (5, 0) is
∴ Distance between the points A (0, 3) and B (5, 0) is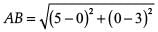
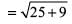
= √34 units
Hence, the required length of diagonal is √34 units.
OR
PQ is tangent and QO is radius at contact point Q.
∴ ∠PQO = 90°
∴ By Pythagoras theorem,
PQ2 = OP2 - OQ2
= 132 - 52 = 169 - 25 = 144
⇒ PQ = 12 cm
∴ ΔOPQ ≅ ΔOPR [SSS congruence]
∴ Area of ΔOPQ = area of ΔOPR
[Since, congruent figures are equal in areas]
Area of quadrilateral QORP = 2 area of ΔOPR
= 2 x 1 / 2 base × height
= RP × OR
= 12 × 5
= 60 cm2
Q.4. What is the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is. (1 Mark)
Ans. Let r1 = 24 cm and r2 = 7 cm
Area of first circle = πr12 = π(24)2 = 576π cm2
Area of second circle = πr22 = (7) = 49 cm2
According to question, Area of circle = Area of first circle + Area of second circle πR2 = 576π +49π
[where, R be radius of circle]
R2 = 625 ⇒ R = 25 cm
Diameter of a circle = 2R = 2 × 25 = 50 cm.
Q.5. If two solid hemispheres of same base radius ‘r’ are joined together along their bases, then curved surface area of this new solid. (1 Mark)
Ans. When two hemispheres of equal radii are joined base to base, new solid becomes sphere and curved surface area of sphere is 4πr2.
Q.6. It is given that ΔABC~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, DE = 12 cm, ÐF = 100° is true or not, justify. (1 Mark)
Ans. Since ΔABC ~ ΔDFE, we have
∠Z = ∠D = 30°, ∠B = ∠F = 100°, ∠C = ∠E = 50°,
Using basic proportionality theorem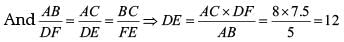
Q.7. What is the coordinates of the point which lies on the perpendicular bisector of the line segment joining the points A(– 2, – 5) and B(2, 5). (1 Mark)
Ans. The perpendicular bisector of any line segment always passes through the mid-point of the line segment.
Mid-point of any line segment which passes through the points (x1, y1) and (x2, y2) is given by 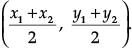
So, Co-ordinates of the mid-point of the line segment joining the points A(– 2, – 5) and B(2, 5) is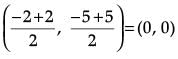
Q.8. If all the zeroes of a cubic polynomial are negative, then what are the signs of all the coefficients and the constant term of the polynomial? (1 Mark)
Ans. If f(x) = ax3 + bx2 + cx + d = 0. Then, for all negative roots, a, b, c and d must have same sign.
Q.9. Find the solution of pair of equations y = 0 and y = – 7 (1 Mark)
OR
If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k? (1 Mark)
Ans. We know that equation of the form y = a is a line parallel to x-axis at a distance 'a' from it. y = 0 is the solution of the x-axis and y = – 7 is the equation of the line parallel to x-axis. So the given pairs of parallel lines has no solution.
OR
For parallel lines (or no solution)
a1 / a2 = b1 / b2 ≠ c1 / c2
⇒ 3 / 2 = 2k / 5 ≠ -2 / 1
⇒ 4k = 15
⇒ k = 15 / 4 or k not equal to – 5
Q.10. If the common difference of an A.P. is 5, then find the value of a18 – a13. (1 Mark)
Ans. In the given A.P., = d = 5
Thus, a18 – a13
= a + 17d – (a + 12d)
= a + 17d – a – 12d
= 5d = 5 × 5 = 25.
Q.11. If we draw any line from the centre of the circle to the tangent, then find the angle between them. (1 Mark)
Ans. By using the theorem, the tangent at any point of a circle is perpendicular to the radius through the point of contact. Hence, angle between them is 90°
Q.12. From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB. (1 Mark)
Ans. 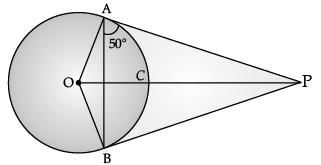
Here, ∠OAB = 90° – 50° = 40° (∵ PA ⊥ OA)
∠OAB = ∠OBA = 40°
(∵ OA and OB are radii)
∴ ∠AOB + 40° + 40° = 180°
∠AOB = 180° – 80° = 100°
Hence ∠AOB = 100°
Q.13. If tan (3x + 30°) = 1, then find the value of x. (1 Mark)
Ans. tan (3x + 30°)= 1 = tan 45°
or, 3x + 30° = 45° or, x = 5°
Q.14. If the circumferences of two concentric circles forming a ring are 88 cm and 66 cm respectively. Find the width of the ring. (1 Mark)
Ans. ∵ Circumference of the outer circle, 2πr1 = 88 cm
∴ r1 = 88 x 7 / 22 x 2 = 14 cm.
∵ Circumference of the inner circle, 2πr2 = 66 cm
∴ r2 = 66 x 7 / 2 x 22 = 21 / 2 cm = 10.5 cm
∴ Width of the ring = r1 – r2
= 14 – 10.5 cm = 3.5 cm.
Q.15. Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere? (1 Mark)
OR
Find the number of solid spheres of diameter 6 cm can be made by melting a solid metallic cylinder of height 45 cm and diameter 4 cm. (1 Mark)
Ans. Let radius of hemisphere be r.
Given, volume of hemisphere = Surface area of hemisphere
or, 2 / 3 πr3 = 3 πr3
or, r = 9 / 2 units
∴ Diameter = 9 / 2 x 2 = 9 units.
OR
Let the number of spheres be n.
Radius of sphere r1 = 3 cm,
radius of cylinder r2 = 2 cm
Volume of n spheres = Volume of cylinder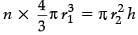
or,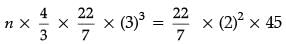
or, 36 n = 180
or, n = 180 / 36 = 5
Thus, the number of solid spheres = 5.
Q.16. Find the median of the data, using an empirical relation between mean, median and mode when it is given that Mode = 12.4 and Mean = 10.5. (1 Mark)
Ans.
Median =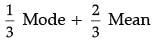
=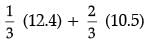
= 12.4 / 3 + 21 / 3
=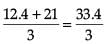
= 33.4 / 3 = 11.13
Section - II
Case study based questions are compulsory. Attempt any four sub parts of each question. Each subpart carries 1 mark
Q.17. Case Study based - 1 :
In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see figure below). A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket.
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket.
(a) What is the distance travelled by competitor to pick 1st potato? (1 Mark)
(i) 10
(ii) 16
(iii) 22
(iv) 48
Ans. (i)
Solution. The distance travelled by the competitor to pick 1st potato = 2 × 5 = 10
(b) What is the distance travelled by competitor to pick 2nd potato? (1 Mark)
(i) 10
(ii) 16
(iii) 22
(iv) 48
Ans. (ii)
Solution. The distance travelled by the competitor to pick 2nd potato = 2 × (5 + 3) = 16
(c) What is the distance travelled by competitor to pick 3rd potato? (1 Mark)
(i) 10
(ii) 16
(iii) 22
(iv) 48
Ans. (iii)
Solution. The distance travelled by the competitor to pick 3rd potato = 2 × (5 + 6) = 22
(d) The given problem is based on which concept? (1 Mark)
(i) AP
(ii) GP
(iii) HP
(iv) None of these
Ans. (i)
Solution. The numbers involved in this case is in AP in which a = 10, d = 6, n = 10
(e) Find the total distance travelled by the competitor? (1 Mark)
(i) 300
(ii) 370
(iii) 730
(iv) 700
Ans. (ii)
Solution.
Since,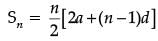 , we have
, we have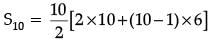
= 5 × [24 + 54]
= 5 × 74 = 370
Thus, the total distance travelled by the competitor to pick all the potatoes is 370 m.
Q.18. Case Study based - 2 :
Ayush Starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter's school and then reaches the office. (Assume that all distances covered are in straight lines). If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at (13, 26) and coordinates are in km.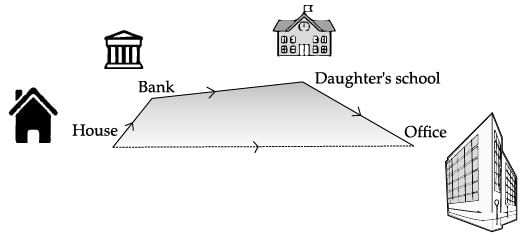
(a) What is the distance between house and bank? (1 Mark)
(i) 5
(ii) 10
(iii) 12
(iv) 27
Ans. (i)
Solution. We know that, Distance between two points (x1, y1) and (x2, y2).
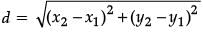
Now, distance between house and bank,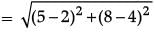
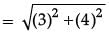
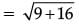
= √25
= 5
(b) What is the distance between Daughter ’s School and bank? (1 Mark)
(i) 5
(ii) 10
(iii) 12
(iv) 27
Ans. (iii)
Solution. Distance between bank and daughter's school,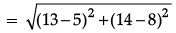
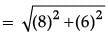
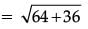
= √100
= 10
(c) What is the distance between house and office? (1 Mark)
(i) 24.6
(ii) 26.4
(iii) 24
(iv) 26
Ans. (ii)
Solution. Distance between house to office,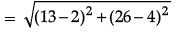
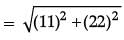
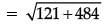
= √605
= 24.59
= 24.6 km
(d) What is the total distance travelled by Ayush to reach the office? (1 Mark)
(i) 5
(ii) 10
(iii) 12
(iv) 27
Ans. (iv)
Solution. Distance between daughter's school and office,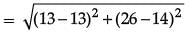
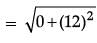
= 12
Total distance (House + Bank + School + Office) travelled = 5 + 10 + 12 = 27 km
(e) What is the extra distance travelled by Ayush? (1 Mark)
(i) 2
(ii) 2.2
(iii) 2.4
(iv) None of these
Ans. (iii)
Solution. Extra distance travelled by Ayush in reaching his office = 27 – 24.6 = 2.4 km.
Q.19. Case Study based - 3 :
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour.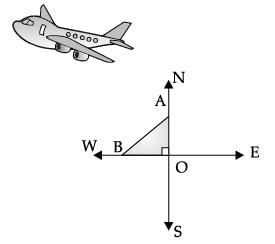
(a) What is the distance travelled by aeroplane towards north after 1 ½ hours? (1 Mark)
(i) 1000
(ii) 1200
(iii) 1500
(iv) 1800
Ans. (iii)
Solution. Distance travelled by the aeroplane towards North,
OA = 1000 x 3 / 2
= 1,500 km
(b) What is the distance travelled by aeroplane towards west after 1 ½ hours? (1 Mark)
(i) 1000
(ii) 1200
(iii) 1500
(iv) 1800
Ans. (iv)
Solution. Distance travelled by the aeroplane towards West,
OB = 1200 x 3 / 2
= 1,800 km
(c) ∠AOB is (1 Mark)
(i) 90°
(ii) 45°
(iii) 30°
(iv) 60°
Ans. (i)
Solution. Angle between North and West direction is always 90°.
(d) How far apart will be the two planes after 1 ½ hours? (1 Mark)
(i) √22,50,000
ii) √32,40,000
(iii) √54,90,000
(iv) None of these
Ans. (iii)
Solution. Since ΔAOB is right triangle, by using Pythagoras Theorem, we have
AB2 = OA2 + OB2
= (1,500)2 + (1,800)2
= 22,50,000 + 32,40,000
= 54,90,000
Thus, the two planes after 1 ½ hours is at a distance of AB = √54,90,000
(e) The given problem is based on which concept? (1 Mark)
(i) Triangles
(ii) Co-ordinate geometry
(iii) Height and Distance
(iv) None of these
Ans. (i)
Q.20. Case Study based - 4 :
A horse is tied to a peg at one corner of a square shaped grass field of sides 15 m by means of a 5 m long rope (see the given figure).
(a) What is the area of the grass field? (1 Mark)
(i) 225 m2
(ii) 225 m
(iii) 255 m2
(iv) 15 m
Ans. (i)
Solution. Area of square = (side)2
= 15 × 15 = 225 m2
(b) The area of that part of the field in which the horse can graze. (1 Mark)
(i) 19.625 m2
(ii) 19.265 m2
(iii) 19 m2
(iv) 78.5 m2
Ans. (i)
Solution. From the figure, it can be observe that the horse can graze a sector of 90° in a circle of 5 m radius.
Area that can be grazed by horse
= Area of sector
=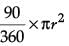
=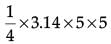
= 19.625 cm2
(c) The grazing area if the rope were 10 m long instead of 5 m. (1 Mark)
(i) 7.85 m2
(ii) 785 m2
(iii) 225 m2
(iv) 78.5 m2
Ans. (iv)
Solution. Area that can be grazed by the horse when length of rope is 10 m long
=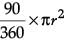
=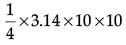
= 78.5 cm2
(d) The increase in the grazing area if the rope were 10 m long instead of 5 m. (1 Mark)
(i) 58.758 m2
(ii) 58.875 m2
(iii) 58 m2
(iv) 78.5 m2
Ans. (ii)
Solution. Increase in grazing area
= (78.5 – 19.625) m2
= 58.875 m2
(e) The given problem is based on which concept? (1 Mark)
(i) Coordinate geometry
(ii) Area related to circles
(iii) Circle
(iv) None of these
Ans. (ii)
Part - B
Section - III
All questions are compulsory. In case of internal choices, attempt any one.
Q.21. Complete the following factor tree and find the composite number x : (2 Mark)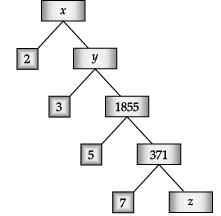
Ans. 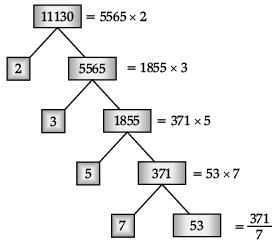 y = 5565
y = 5565
z = 53
∴ x = 11,130
Q.22. ABC is a right triangle, right angled at C. Let BC = a, CA = b, AB = c and p be the length of perpendicular from C to AB. Prove that cp = ab. (2 Mark)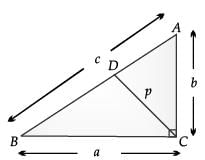
OR
In the figure, PQRS is a trapezium in which PQ || RS. On PQ and RS, there are points E and F respectively such that EF intersects SQ at G. Prove that EQ × GS = GQ × FS. (2 Mark)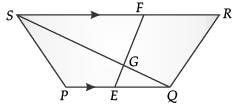
Ans. Let CD ⊥ AB,
Then CD = p
Area of ΔABC = 1 / 2 x base x height
or, Area of ΔABC with base AB
= 1 / 2 x AB x CD
= 1 / 2 cp
Also, Area of ΔABC with base BC
= 1 / 2 x BC x AC
= 1 / 2 ab
So, 1 / 2 cp = 1 / 2 ab
or, cp = ab.
Hence proved.
OR
In ΔGEQ and ΔGFS
∠EGQ = ∠FGS
(vert. opp. angles)
∠EQG = ∠FSG (alt. angles)
∴ ΔGEQ ~ ΔGFS (AA similarity)
or, EQ / FS = GQ / GS
or, EQ × GS = GQ × FS.
Q.23. Find cosec 30° and cos 60° geometrically. (2 Mark)
OR
Prove that :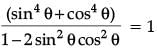 (2 Mark)
(2 Mark)
Ans. 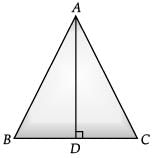 Let a triangle ABC with each side equal to 2a.
Let a triangle ABC with each side equal to 2a.
∠A = ∠B = ∠C = 60°
Draw AD perpendicular to BC
ΔBDA ≌ ΔCDA by RHS congruence criteria
BD = CD
∠BAD = ∠CAD = 30° by CPCT
In ΔBDA, cosec 30° = AB / BD = 2a / a = 2
and cos 60° = BD / AB = a / 2a = 1 / 2
LHS =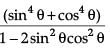
=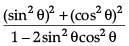
=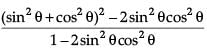
=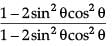
= 1
= RHS
Q.24. From the top of light house, 40 m above the water, the angle of depression of a small boat is 60°. Find how far the boat is from the base of the light house. (2 Mark)
Ans. Let AB be the light house and C be the position of the boat.
Since, ∠PAC = 60° ∴ ∠ACB = 60°
Let BC be x m.
In ΔABC, AB / BC = tan 60°
⇒ 40 / x = √3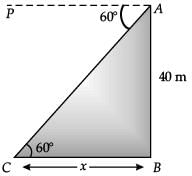 ⇒
⇒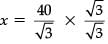
= 40√3 / 3 m
Hence, the boat is 40√3 / 3 m away from the foot of the light house.
Q.25. Find the area of the square that can be inscribed in a circle of radius 8 cm. (2 Mark)
Ans. Diameter of the circle = diagonal of square
= 2 × 8 = 16 cm
Let x be the side of square.
∴ x√2 = 16 or, x = 8√2
Area of square = x2 = (8√2)2
= 128 cm2
Q.26. The mean and median of 100 observations are 50 and 52 respectively. The value of the largest observation is 100. It was later found that it is 110 not 100. Find the true mean and median. (2 Mark)
Ans. Mean = Σfx / Σf
⇒ 50 = Σfx / 100
⇒ Σfx = 5000
Correct, Σfx' = 5000 – 100 + 110 = 5010
∴ Correct Mean = 5010 / 100
= 50.1
Median will remain same i.e. median = 52
Section - IV
All questions are compulsory. In case of internal choices, attempt any one.
Q.27. Determine the values of m and n so that the following system of linear equations have infinite number of solutions : (3 Mark)
(2m – 1)x + 3y – 5 = 0
and 3x + (n – 1)y – 2 = 0
OR
Solve for x and y : (3 Mark)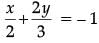
and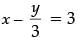
Ans. We have, for equation
(2m – 1)x + 3y – 5 = 0 ...(i)
a1 = 2m – 1, b1 = 3 and c1 = – 5
and for equation
3x + (n – 1)y – 2 = 0 ...(ii)
a2 = 3, b2 = (n – 1) and c2 = –2
For a pair of linear equations to have infinite number of solutions
a1 / a2 = b1 / b2 = c1 / c2
or 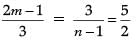
or 2(2m – 1) = 15 and 5(n – 1) = 6
Hence, m = 17 / 4 and n = 11 / 5
OR
Given,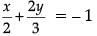
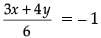
or, 3x + 4y = – 6 ...(i)
and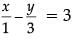
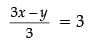
or, 3x – y = 9 ...(ii)
On subtracting eqn. (ii) from eqn. (i),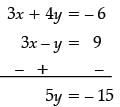
∴ y = – 3
Putting y = – 3 in eq (i), we get
3x + 4 (– 3) = – 6
3x – 12 = – 6
3x = 12 – 6
3x = 6
∴ x = 2
Hence, x = 2 and y = – 3.
Q.28. Write all the values of p for which the quadratic equation x2 + px + 16 = 0 has equal roots. Find the roots of the equation so obtained. (3 Mark)
Ans. x2 + px + 16 = 0 have equal roots if
D = p2 – 4(16)(1) = 0
p2 = 64 ⇒ p = ± 8
∴ x2 ± 8x + 16 = 0 ⇒ (x ± 4)2 = 0
x ± 4 = 0
∴ Roots are x = – 4 and x = 4
Detailed Solution :
Given quadratic equation,
x2 + px + 16 = 0 ...(i)
If this equation has equal roots, then discriminant value is zero
i.e., D = b2 – 4ac = 0 ...(ii)
Now, comparing the given quadratic equation with
ax2 + bx + c = 0, we get
a = 1, b = p and c =16
∴ From eq (ii), p2 – 4 × 1 × 16 = 0
⇒ þ2 = 64
⇒ p = ±8
When þ = 8, From eq (i),
x2 + 8x +16 = 0
⇒ x2 + 4x + 4x +16 = 0
⇒ x(x + 4) + 4(x + 4) = 0
⇒ (x + 4)(x + 4) = 0
⇒ x = –4, –4
Hence, roots are –4 and –4. when p = – 8,
From eg (i), x2 – 8x + 16 = 0
⇒ x2 – 4x – 4x +16 = 0
⇒ x(x – 4) –4(x – 4) = 0
⇒ (x – 4) (x – 4) = 0
⇒ x = 4, 4
Hence, the required roots are either – 4, – 4 or 4, 4
Q.29. If the sum of first m terms of an AP is the same as the sum of its first n terms, show that the sum of its first (m + n) terms is zero. (3 Mark)
Ans. 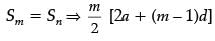
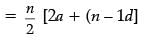
⇒ 2a (m – n) + d (m2 – m – n2 + n) = 0
⇒ (m – n) [2a + (m + n – 1) d] = 0
or Sm+n = 0
Detailed Solution :
Sum of first m terms = Sum of first n terms
⇒ Sm = Sn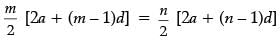
m [2a + (m – 1) d] = n [2a + (n – 1) d]
m [2a + (m – 1) d] – n [2a + (n – 1) d] = 0
2a (m – n) + [m (m – 1) – n (n – 1)] d = 0
2a (m – n) + [m2 – m – n2 + n] d = 0
2a (m – n) + [(m – n) (m + n) – (m – n)] d = 0
(m – n) [2a + (m + n – 1) d] = 0
Here, (m – n) is not equal to zero.
So, [2a + (m + n – 1)d] = 0
Hence, Sm + n = 0.
Q.30. A vertical row of trees 12 m long casts a shadow 8 m long on the ground, At the same time a tower casts the shadow 40 m long on the ground. (3 Mark)
Ans. (i) Let AB be the vertical tree and AC be its shadow. Also, let DE be the vertical tower and DF be its shadow. Join BC and EF. Let DE = x.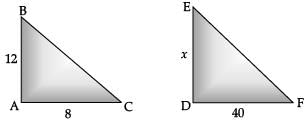 We have
We have
AB = 12 m
AC = 8 m
and DF = 40 m
In ΔABC and ΔDEF,
∠A = ∠D = 90°
Since, the sun casts equal angle at the same time
∠C = ∠F
Therefore by AA criterion of similarity, we have
ΔABC ~ ΔDEF
or, AB / DE = AC / DF
or, 12 / x = 8 / 40
or, 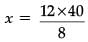
or, x = 60 m. or, height of tower =60 m. 1
(ii) Similar Triangles.
Q.31. AB is a chord of circle with centre O. At B, a tangent PB is drawn such that its length is 24 cm. The distance of P from the centre is 26 cm. If the chord AB is 16 cm, find its distance from the centre. (3 Mark)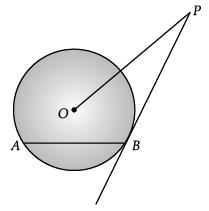
OR
Prove that the lengths of two tangents drawn from an external point to a circle are equal. (3 Mark)
Ans. Given, AB is a chord of circle with centre O and tangent PB = 24 cm, OP = 26 cm.
Construction : Join O to B and draw OC ⊥ AB.
By Pythagoras theorem,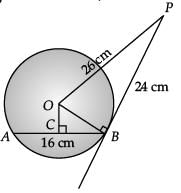
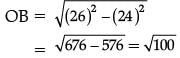
= 10 cm
Now, in ΔOBC, BC = 1 / 2 AB = 16 / 2 = 8 (Perpendicular drawn from the centre to a chord bisects it.)
OR
Given : AP and BP are tangents of circle having centre O.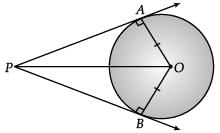 To Prove : AP = BP
To Prove : AP = BP
Construction : Join OP, AO and BO
Proof : ΔOAP and ΔOBP
OA = OB (Radius of circle)
OP = OP (Common side)
∠OAP = ∠OBP = 90°
(Radius – tangent angle)
ΔOAP ≌ ΔOBP
(RHS congruency rule)
AP = BP (CPCT)
Hence Proved.
Q.32. One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting (3 Mark)
(a) Non face card,
(b) Black king or a Red queen,
(c) Spade card.
Ans. (a) Total number of cards = 52
Number of non-face cards
= 52 – 12 = 40
P(non-face cards) = 40 / 52 = 10 / 13
(b) Number of black kings = 2
Number of red queens = 2
P(a black Kind or a red queen) = 4 / 52 = 1 / 13
(c) Number of spade cards = 13
P (Spade cards) = 13 / 52 = 1 / 4
Q.33. Prove that : (cot θ – cosec θ)2 =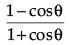 (3 Mark)
(3 Mark)
Ans. LHS = (cot θ – cosec θ)2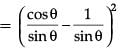
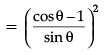
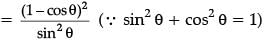
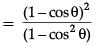
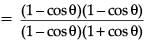
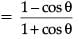
= RHS
Hence proved.
Section - V
All questions are compulsory. In case of internal choices, attempt any one.
Q.34. If roots of the quadratic equation x2 + 2px + mn = 0 are real and equal, show that the roots of the quadratic equation x2 – 2(m + n)x + (m2 + n2 + 2p2) = 0 are also equal. (5 Mark)
Ans. For equal roots of x2 + 2px + mn = 0,
D = 0
4p2 – 4mn = 0
⇒ p2 = mn ...(i)
For equal roots of
x2 – 2 (m + n)x + (m2 + n2 + 2p2) = 0,
4(m + n)2 – 4(m2 + n2 + 2p2) = 0,
m2 + n2 + 2mn – m2 – n2 – 2(mn) = 0 (From (i))
∴ If roots of x2 + 2px + mn = 0 are equal, then those of x2 – 2a(m + n)x + (m2 + n2 + 2p2) = 0 are also equal.
Q.35. If P(9a – 2, – b) divides the line segment joining A(3a + 1, – 3) and B(8a, 5) in the ratio 3 : 1. Find the values of a and b. (5 Mark)
Ans. By section formula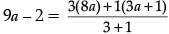 ...(i)
...(i)
and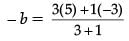 ...(ii)
...(ii)
From (ii),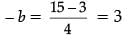
b = – 3
From (i),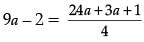
4(9a – 2) = 27a + 1
36a – 8 = 27a + 1
9a = 9 a = 1
Q.36. Two points A and B are on the same side of a tower and in the same straight line with its base. The angle of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between these points. (5 Mark)
OR
A man on a cliff observes a boat at an angle of depression of 30° which is approaching the shore to the point immediately beneath the observer with a uniform speed. Six minutes later, the angle of depression of the boat is found to be 60°. Find : (5 Mark)
(i) Time taken by boat to reach the shore.
(ii) Which concept used in this question?
Ans. 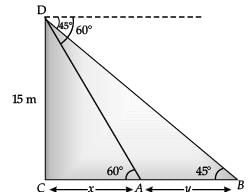 In ΔDCA, DC / CA = tan 60°
In ΔDCA, DC / CA = tan 60°
⇒ 15 / x = √3
⇒ x = 15 / √3
⇒ x = 15√3
In ΔDCB, DC / CB = tan 45° x = 15 / x + y = 1
⇒ x + y = 15
⇒ 15√3 + y = 15
⇒ y = 15 − 15√3
= 5 (3 − √3) m
Hence, the distance between the points
= 5 (3 − √3) m
OR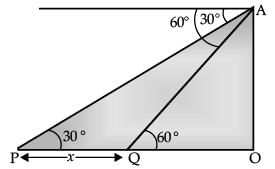
(i) Let OA be the cliff and P be the initial position of the boat when the angle of depression is 30°. After 6 minutes the boat reaches to Q such that the angle of depression at Q is 60°.
Let PQ = x m.
In ∠POA and ∠QOA, we have
tan 30°= OA / OP and tan 60° = OA / OQ
⇒ 1 / √3 = OA / OP and √3 = OA / OQ
⇒ OA = OP / √3 and OA = √3OQ
⇒ OP / √3 = √3OQ
⇒ OP = 3OQ
⇒ PQ = OP – OQ
= OP - OP / 3
= 2 / 3 OP [∵ OQ = 1 / 3 OP]
Let the speed of the boat be v m/minute, then
PQ = Distance travelled by the boat in 6 minutes
⇒ PQ = 6v
⇒ 2 / 3(OP) = 6v
⇒ OP = 9v
∴ Time taken by the boat to reach at the shore is given by,
T = OP / v
⇒ T = 9v / v
= 9 minutes
(ii) Height and distance.
|
127 videos|550 docs|75 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Standard) - 3 - Mathematics (Maths) Class 10
| 1. What topics are covered in the Class 10 Mathematics CBSE Sample Question Paper for 2020-21? |  |
| 2. How can students effectively prepare for the CBSE Class 10 Mathematics exam using the sample question paper? |  |
| 3. What is the format of the CBSE Class 10 Mathematics exam, and how does the sample question paper reflect this format? |  |
| 4. Are there any specific marking schemes or guidelines provided in the CBSE sample question paper for Mathematics? |  |
| 5. Where can students find additional resources or practice materials for the Class 10 Mathematics syllabus? |  |

















