Class 10 Mathematics: CBSE Sample Question Paper- Term II (2021-22) - 5 | CBSE Sample Papers For Class 10 PDF Download
| Table of contents |

|
| Class-X |

|
| Time: 120 |

|
| Minutes |

|
| M.M: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-X
Time: 120
Minutes
M.M: 40
General Instructions:
Read the following instructions very carefully and strictly follow them:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section - A
Q.1. Which term of the A.P. 27, 24, 21, ...... is zero ?
OR
In an Arithmetic Progression, if d = – 4, n = 7, an = 4, then find a.
Since, nth term (an) = a + (n – 1)d
Let an be zero an = 0
0 = 27 + (n – 1)(– 3)
30 = 3n
n = 10
10th term of the given A.P. is zero.
Detailed Solution:
Given A.P. = 27, 24, 21, ........... .
Here, a = 27 and d = 24 – 27 = – 3
and, an = 0
∴ an = a + (n – 1)d
⇒ 0 = 27 + (n – 1)(– 3)
⇒ – 3n + 3 = – 27
⇒ – 3n = – 27 – 3 = – 30
⇒ n = 10.
OR
Since, an = a + (n – 1)d
4 = a + 6 × (– 4)
a = 28
Detailed Solution:
We have, d = – 4, n = 7 and an = 4∴ an = a + (n – 1)d
⇒ 4 = a + (7 – 1)(– 4)
⇒ 4 = a + 6 (– 4)
⇒ = a – 24
⇒ a = 4 + 24
⇒ a = 28.
Q.2. Find the roots of the equation x2 + 7x + 10 = 0 by using quadratic formula.
Given, x2 + 7x + 10 = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = 7 and c = 10
∴
⇒
⇒
⇒
⇒
⇒ x = – 2 or – 5
Hence, the roots of the given equation are – 2 and – 5.
Q.3. In the following, if PQ = 28 cm, then find the perimeter of ΔPLM.
∵ PQ = PT
PL + LQ = PM + MT
PL + LN = PM + MN (LQ = LN, MT = MN)
(Tangents to a circle from a common point)
Perimeter (ΔPLM) = PL + LM + PM
= PL + LN + MN + PM
= 2(PL + LN)
= 2(PL + LQ)
= 2 × 28 = 56 cm
Detailed Solution:
Given, PQ = 28 cm
∴ PQ = PT (Length of tangents from an external point are equal)
i.e., PQ = PT = 28 cm
According to figure,
Let LQ = x, then
PL = (28 – x) cm
and let MT = y, then
PM = (28 – y) cm
and LM = LN + NM
= x + yNow, the perimeter of ΔPLM = PL + LM + PM
= (28 – x) + (x + y) + (28 – y)
= 28 + 28 = 56 cm.
Q.4. From a solid right circular cylinder of height 14 cm and base radius 6 cm, a right circular cone of same height and same base removed. Find the volume of the remaining solid.
Given, Height (h) = 14 cm
Base radius (r) = 6 cm
Volume of the remaining solid = Volume of a right circular cylinder – Volume of a right circular cone
= πr2h – (1/3)πr2h
= 2/3 πr2h
= (2/3) x (22/7) x 6 x 6 x 14
=1056 cm3.
Q.5. Compute the mode for the following frequency distribution:
Here, modal class = 12 – 16
∴ l1 = 12, f1 = 17, f0 = 9, f2 = 12 and h = 4
Mode =
= 12 + ((8 x 4)/13)
= 12 + 2.46 = 14.46. (Approx)
Q.6. For what values of k, the given quadratic equation 9x2 + 6kx + 4 = 0 has equal roots ?
OR
Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60. Find the numbers.
9x2 + 6kx + 4 = 0
For equal roots, b2 – 4ac = 0
Discriminant, D = 0
So, (6k)2 – 4 × 9 × 4 = 0
36k2 = 144
k2 = 4
k = ± 2
Detailed Solution:
Given, 9x2 + 6kx + 4 = 0.
Comparing with ax2 + bx + c = 0,
we get a = 9, b = 6k, c = 4
Since, Discriminant, D = b2 – 4ac
For equal roots, D = 0
b2 – 4ac = 0
⇒ (6k)2 – 4 × 9 × 4 = 0
⇒ 36k2 – 144 = 0
⇒ 36k2 = 144
⇒ k2 = 4⇒ k = ± 2
OR
Let the three consecutive natural numbers be x, x + 1 and x + 2.
∴ (x + 1)2 = (x + 2)2 – (x)2 + 60
⇒ x2 + 2x + 1 = x2 + 4x + 4 – x2 + 60
⇒ x2 – 2x – 63 = 0
⇒ x2 – 9x + 7x – 63 = 0
⇒ x(x – 9) + 7(x – 9) = 0
⇒ (x – 9)(x + 7) = 0
Thus, x = 9 or x = – 7
Rejecting – 7, we get x = 9
Hence, three numbers are 9, 10 and 11.
Section - B
Q.7. On annual day of a school, 400 students participated in the function. Frequency distribution showing their ages is as shown in the following table :
Find mean and median of the above data.
Let a = Assumed mean = 12
Mean,
Mean =
Median class = N/2
= 400/2 = 200 which lie in class 09 – 11.
Median =
Median
Q.8. Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.
Steps of construction :
(i) Draw a line segment AB = 7 cm.
(ii) With A as centre and radius 3 cm draw a circle.
(iii) With B as centre and radius 2 cm draw another circle.
(iv) Taking AB as diameter and draw perpendicular bisector, which intersects first two circles at P and Q, R and S.
(v) Join B to P and Q, A to R and S.
Hence, BP, BQ, AR and AS are the required tangents.
Q.9. The mean of the following distribution is 53. Find the missing frequency k?
Given, Mean = 53
∴ Mean =
⇒ 53 =
⇒ 53(72 + k) = 3340 + 70k
= 3816 + 53k = 3340 + 70k
⇒ 70k – 53k = 3816 – 3340
⇒ 17k = 476
⇒ k = 28
Hence, value of k is 28.
Q.10. Two points A and B are on the same side of a tower and in the same straight line with its base. The angle of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between these points.
OR
A moving boat observed from the top of a 150 m high cliff, moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat.
Let the distance between these points be y m.
Also, let CA be x m.In ΔDCA, ∠C = 90°
DC/CA = tan 60°
⇒ 15/x = √3
⇒ x = 15/√3
⇒ x = 5√3
In ΔDCB, ∠C = 90°
DC/CB = tan 45° = 15/(x+y) = 1
⇒ x + y = 15
⇒ 5√3 + y = 15
⇒ y = 15 − 5√3
= 5(3 − √3) m
Hence, the distance between the points = 5 (3 − √3) m.
ORLet the speed of the boat be x m/min.
∴ Distance covered in 2 minutes = 2x
∴ CD = 2x
Let BC be y m.
In ΔABC, ∠B = 90°
AB/BC = tan 60°
⇒ 150/y = √3
⇒ y =150/√3
⇒ y = 50√3 m. ...(i)
In ΔABD, ∠B = 90°
AB/BD = tan 45°
⇒ 150/(y + 2x) = 1
⇒ y + 2x = 150 ...(ii)
Substituting the value of y from (i) in (ii),
50√3 +2x = 150
2x = 150 − 50√3
2x = 50 (3 −√3)
x = 25 (3 − √3) m.
Speed of the boat = 25 (3 − √3) m/min.
= 3/2(3 - √3) km/h
= 19.02 km/h
Section - C
Q.11. Rampal decided to donate canvas for 10 tents conical in shape with base diameter 14 m and height 24 m to a centre for handicapped person's welfare. If the cost of 2 m wide canvas is ₹ 40 per metre, find the amount by which Rampal helped the centre.
Diameter of tent = 14 m and height = 24 m
∴ radius of tent = 7 m
Slant height =
Surface area of the tent = πrl
= (22/7) x 7 x 25
= 550 m2
Surface area of 10 tents = 550 × 10 = 5500 m2
Total cost = 5500 x (40/2)
= ₹ 1,10,000
Hence, the amount by which Rampal helped the centre = ₹ 1,10,000.
Q.12. In the given figure, two tangents TP and TQ are drawn to circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.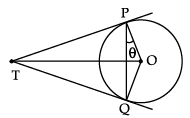
OR
a, b and c are the sides of a right triangle, where c is the hypotenuse. A circle, of radius r, touches the sides of the triangle. Prove that r = (a + b - c)/2.
Let ∠OPQ be θ, then
∠TPQ = 90° – θ
Since, TP = TQ
∴ ∠TQP = 90° – θ (opposite angles of equal sides)Now, ∠TPQ + ∠TQP + ∠PTQ = 180° (Angle sum property of a Triangle)
⇒ 90° – θ + 90° – θ + ∠ PTQ = 180°
⇒ ∠PTQ = 180° – 180° + 2θ
⇒ ∠PTQ = 2θ
Hence, ∠PTQ = 2∠OPQ Hence Proved.OR
Let circle touches CB at M, CA at N and AB at P.
Now OM ⊥ CB and ON ⊥ AC
(radius ⊥ tangent)
OM = ON (radii)
CM = CN (Tangents)
∴ OMCN is a square.
Let OM = r = CM = CN
AN = AP, CN= CM and BM = BP (tangent from external point)
AN = AP
⇒ AC – CN = AB – BP
b – r = c – BM
b – r = c – (a – r)
b – r = c – a + r
∴ 2r = a + b – c
r = (a + b – c)/2. Hence Proved.
Case Study-1
Q.13. A Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka ,them being Nanda Devi(height 7, 816 m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite, to the top of Nanda Devi and Mullayanagiri are 30° and 60° respectively. If the distance between the peaks of two mountains is 1937 km, and the satellite is vertically above the midpoint of the distance between the two mountains.
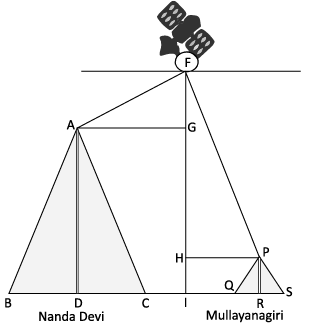
(i) Find the distance of the satellite from the top of Nanda Devi.
(ii) Find the total distance of the satellite from the top of Mullayanagiri.
(i)
In ΔFGA, AG = (1937/2) km
cos θ = AG/AF
AF = 1937/√3
AF = 1118.36 km
(ii) For ΔFPH,
cos θ = PH/FP
cos 60° = 1937/2FP
1/2 = 1937/2FP
FP = 1937 km.
Case Study-2
Q.14. Your elder brother wants to buy a car and plans to take loan from a bank for his car. He repays his total loan of ₹ 1,18,000 by paying every month starting with the first instalment of ₹ 1000. If he increases the instalment by ₹ 100 every month, answer the following:

(i) Find the amount paid by him in 30th installment.
(ii) The amount paid by him in the 30 installments.
(i) First term a = 1000
Common difference d = 100
30th term, a30 = a + (n – 1)d
= 1000 + (30 – 1)100
= 1000 + 2900
= ₹ 3900
(ii) Sum of 30 installments
= (n/2)[2a + (n - 1)d]
= (30/2)[2 x 1000 + (30 - 1)100]
= 15[2000 + 2900]
= 15[2000 + 2900]
= 73500
Total amount paid in 30 installments = ₹ 73500
|
303 docs|7 tests
|

|
Explore Courses for Class 10 exam
|

|












































