Class 10 Mathematics: CBSE Sample Question Paper- Term II (2021-22) - 4 | CBSE Sample Papers For Class 10 PDF Download
| Table of contents |

|
| Class-X |

|
| Time: 120 |

|
| Minutes |

|
| M.M: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-X
Time: 120
Minutes
M.M: 40
General Instructions:
Read the following instructions very carefully and strictly follow them:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section - A
Q.1. Find the value of a25 - a15 for the AP: 6, 9, 12, 15, ………..
OR
If 7 times the seventh term of the AP is equal to 5 times the fifth term, then find the value of its 12th term.
a = 6, d = 3 ;
a25 = 6 + 24(3) = 78
a15 = 6 + 14(3) = 48
a25 – a15 = 78 – 48
a25 – a15 = 30
OR
7(a + 6d) = 5(a + 4d)
⇒ 2a + 22d = 0
⇒ a + 11d = 0
⇒ t12 = 0
Detailed Solution:
6, 9, 12, 15, ....... is the given A.P.
First term = a = 6
Common Difference = d = 9 – 6 = 3
nth term = an = a + (n – 1)d
25th term = a25
= 6 + (25 – 1) × 3
= 6 + (24) × 3
= 6 + 72
= 78
15th term = a15
= 6 + (15 – 1) × 3
= 6 + (14) × 3
= 6 + 42
= 48
a25 – a15 = 78 – 48 = 30
OR
Let 'a' and 'd' be the first term and common difference of AP
nth term = an = a + (n – 1)d
7th term = a7 = a + (7 – 1)d = a + 6d
5th term = a5 = a + (5 – 1)d = a + 4d
According to the Questions,
7a7 = 5a5
7(a + 6d) = 5(a + 4d)
7a + 42d = 5a + 20d
7a – 5a + 42d – 20d = 0
2a + 22d = 0
2(a + 11d) = 0
a + 11d = 0 ...(i)
12th term = a12
= a + 11d
= 0 From (i)
Hence, 12th term is zero.
Q.2. Find the value of m so that the quadratic equation mx(5x – 6) + q = 0 has two equal roots.
Given 5mx2 – 6mx + 9 = 0
Since, b2 – 4ac = 0
for equal roots
(– 6 m)2 – 4 (5 m) (9) = 0
⇒ 36m(m – 5) = 0
⇒ m = 0, 5 ; rejecting m = 0,
we get m = 5
Detailed Solution:
Since, mx (5x – 6) + 9 = 0 has equal roots
∴ Discriminant = 0
⇒ b2 – 4ac = 0 ...(i)
Quadratic equation can be written as 5mx2 – 6mx + 9 = 0
Here, a = 5m, b = – 6m, c = 9
Put in (i),
(6m)2 – 4(5 m)(9) = 0 (m = 0)
= 36m2 – 180m = 0 or m = 5
= 36 m(m – 5) = 0
Either m = 0 or m = 5
Since, m = 0 is not possible
Hence, m = 5.
Q.3. From a point P, two tangents PA and PB are drawn to a circle C(0, r).
If OP = 2r, then find ∠APB. What type of triangle is APB?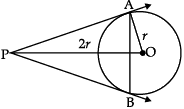
Let ∠APO = θ
sin θ = OA/OP = 1/2 ⇒ θ = 30°
⇒ ∠APB = 2θ = 60°
Also ∠PAB = ∠PBA = 60° (∴ PA = PB)
⇒ ∆APB is equilateralDetailed Solution:
Radius of given circle OA = r units
Let, ∠APO = θ
Radius is always perpendicular to tangent
= OA ⊥ AP
So, ∠OAP = 90°
∴ ∆OAP is a right angled triangle
In ∆OAP,
sin θ = OA/OP
sin θ = r/2r = 1/2
sin θ = sin 30°
⇒ θ = 30°
∠APO = 30°
∠APB = 2 × ∠APO = 2 × 30° = 60°
PA = PB [Length of tangents from an external point are equal in length]
Let, ∠ABP = ∠BAP = x
So, from ∆APB,
∠APB + ∠ABP + ∠BAP = 180° [Angle sum property of triangle]
60° + x + x = 180°
or x = 60°
∴ ∆APB is equilateral triangle.
Q.4. The curved surface area of a right circular cone is 12320 cm². If the radius of its base is 56 cm, then find its height.
CSA (cone) = πrl = 12320 cm2
(22/7) x 56 x l = 12320
l = 70 cm
h = √(702 - 562) = 42 cm
Detailed Solution:
Let Height of cone = h
Radius of cone = 56 cm
C.S.A of cone = 12320 cm2
Let slant height of cone = l cm
Curved surface area of cone = πrl
⇒ 12320 = (22/7) x 56 x l
⇒
⇒ l = 70 cm
Now, l2 = h2 + r2
⇒ (70)2 = h2 + (56)2
⇒ h2 = 4900 – 3136
⇒ h2 = 1764
⇒ h2 = 422
⇒ h = 42 cm
Q.5. Mrs. Garg recorded the marks obtained by her students in the following table. She calculated the modal marks of the students of the class as 45. While printing the data, a blank was left. Find the missing frequency in the table given below.
Modal class is 40 – 60, l = 40,
h = 20, f1 =?,
f0 = 10, f2 = 6
45 = 40 + 20 ×
⇒
⇒ 2f1 – 16 = 4f1 – 40
⇒ f1 = 12
Detailed Solution:
Mode = 45
⇒ Modal class = 40 – 60
Lower limit of modal class (l) = 40
Size of modal class (h) = 20
Frequency corresponding to modal class (F1) = x
Frequency preceding to modal class (F0) = 10
Frequency preceding to modal class (F2) = 6
Mode =
⇒
⇒
⇒
⇒ 2 F1 – 16 = 4 F1 – 40
⇒ 2 F1 – 4 F1 = – 40 + 16
⇒ – 2 F1 = – 24
⇒ F1 = 12
Q.6. If Ritu were younger by 5 years than what she really is, then the square of her age would have been 11 more than five times her present age. What is her present age?
OR
Solve for x : 9x2 – 6px + (p2 – q2) = 0
Let the present age of Ritu be x years
(x – 5)2 = 5x + 11
x2 – 15x + 14 = 0
(x – 14) (x – 1) = 0
⇒ x = 1 or 14
x = 14 years (rejecting x = 1 as in that case Ritu's age 5 years ago will be – ve)
OR
9x2 – 6px + (p2 – q2) = 0
a = 9, b = –6p, c = p2 – q2
D = b2 – 4ac
= (–6p)2 – 4(9) (p2 – q2)
= 36q2
Detailed Solution:
Let present age of Ritu = x years
As per question given the following equation can be formed:
⇒ (x –5)2 = 11 + 5x
⇒ x2 – 10x + 25 = 11 + 5x
⇒ x2 – 10x – 5x + 25 – 11 = 0
⇒ x2 – 15x + 14 = 0
⇒ x2 – 14x – 1x + 14 = 0
⇒ x(x – 14) – 1(x – 14) = 0
⇒ (x – 14) (x – 1) = 0
⇒ x – 14 = 0, x – 1 = 0
x = 14, x = 1
Since, her age can't be 1, so her present age will be 14 years.
OR
9x2 – 6px + (p2 – q2) = 0
In comparing with
ax2 + bx + c = 0
a = 9, b = – 6 p, c = p2 – q2
Solve by quadratic formula,
D = b2 – 4ac
= (– 6p)2 – 4(9)(p2 – q2)
= 36p2 – 36p2 + 36q2
= 36q2
Now,
∴ x =
Section - B
Q.7. The table below show the salaries of 280 persons :
Calculate the median salary of the data.
280/2 = N/2 = 140.
Median class = 10 – 15.
Median = l + (h/f)((N/2) - c.f.)
= 10 + (5/133)(140-49)
= 10 +
= 13.42
Hence, median salary is ₹ 13.42 thousand or ₹ 13420 (approx).
Q.8. Draw two tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
Steps of construction :
(i) Draw a circle of radius 4 cm with O as centre.
(ii) Draw two radii OA and OB inclined to each other at an angle of 120°.
(iii) Draw AP ⊥ OA at A and BP ⊥ OB at B. Which meet at P.
(iv) PA and PB are the required tangents inclined to each other an angle of 60°.
Q.9. Daily wages of 110 workers, obtained in a survey, are tabulated below :
Compute the mean daily wages of these workers.
Mean, x =
Hence, mean daily: wages are ₹ 170.182 (Approx).
Q.10. Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point in between them on the road, the angles of elevation of the top of poles are 60° and 30° respectively. Find the height of the poles and the distances of the point P from the poles.
OR
From a point P on the ground, the angle of elevation of the top of a tower is 30° and that of the top of the flag-staff fixed on the top of the tower is 45°. If the length of the flag-staff is 5 m, find the height of the tower. (Use √3 = 1.732)
Let two poles be AB and CD, then AB = CD = h
In ∆ABP, ∠A = 90°
h/x = tan 60˚= √3 ...(i)
In ∆PCD, ∠C = 90°...(ii)
Dividing (i) by (ii), we get
⇒ 3x = 80 – x
or 4x = 80
⇒ x = 20 m.
and h = 20√3 m.
∴ Height of poles is 20√3 m and the distances of P are 20 m and 60 m from poles.
OR
Let AB be a tower and BC be a flagstaff.
According to question,
In ∆PAC, ∠A = 90°
AC/AP = tan 45° = 1⇒ x + 5 = y ...(i)
In ∆PAB, ∠A = 90°
x/y = tan 30° = 1/√3
⇒
= 13.66/2
= 6.83
∴ Height of tower = 6.83 m
Section - C
Q.11. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in fig. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm. Find the total surface area of the article.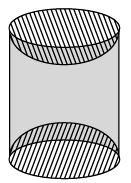
Total surface Area of article = CSA of cylinder + CSA of 2 hemispheres
CSA of cylinder = 2πrh
= 2 x (22/7) x 3.5 x 10 = 220 cm2
Surface area of two hemispherical scoops = 4πr2
= 4 × (22/7) x 3.5 x 3.5
= 154 cm2
∴ Total surface area of article = 220 + 154 = 374 cm2
Q.12. If the radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
OR
In Fig. O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.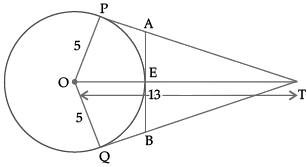
Here, radii of two concentric circles,
OC = 4 cm and
OB = 5 cm
In right angled ΔOBC, ∠C = 90°
CO2 + BC2 = OB2 (Using Pythagoras theorem)
42 + BC2 = 52
16 + BC2 = 25
BC2 = 25 – 16
BC2 = 9
BC = 3 cmSince, AB is the chord and OC⊥AB, that divides AB in two equal parts
Hence, AB = 2 × BC
= 2 × 3
= 64 cm
OR
and TE = OT – OE = 13 – 5 = 8 cm
Let PA = AE = x. (Tangents)
Then, TA2 = TE2 + EA2
or, (12 – x)2 = 82 + x2
24x = 80
or, x = 3.3 cm. (Approx.)
Thus AB = 2 × x = 2 × 3·3
= 6.6 cm. (Approx.)
Case Study-1
Q.13. A group of students of class X visited India Gate on an education trip. The teacher and students had interest in history as well. The teacher narrated that India Gate, official name Delhi Memorial, originally called All-India War Memorial, monumental sandstone arch in New Delhi, dedicated to the troops of British India who died in wars fought between 1914 and 1919. The teacher also said that India Gate, which is located at the eastern end of the Rajpath (formerly called the Kings way), is about 138 feet (42 metres) in height.
(i) What is the angle of elevation if they are standing at a distance of 42 m away from the monument ?
(ii) They want to see the tower at an angle of 60°. So, they want to know the distance where they should stand and hence find the distance.
(i) Height of India gate = 42 m
Distance between students and Indian gate = 42 mNow, ΔABC, ∠B = 90°
tan θ= AB/BC
tan θ = 42/42
tan θ = 1
tan θ = tan 45°
θ = 45°
Hence, angle of elevation = 45°.
(ii) Height of India gate = 42 m
Angle = 60°
Let the distance between students and India gate = x m.Now, In ΔABC, ∠B = 90°
tan θ = AB/BC
tan 60° = 42/x
√3 = 42/x
x =42/√3
= 14√3 m = 25.24 m.
Case Study- 2
Q.14. Your friend Veer wants to participate in a 200 m race. He can currently run that distance in 51 seconds and with each day of practice it takes him 2 seconds less. He wants to do in 31 seconds.
(i) Write in AP for the given situation.
(ii) What is the minimum number of days he needs to practice till his goal is achieved?
(i) a = 51
d = – 2
For an AP, the common difference of each term will be same.
First term (a) = 51 seconds
Common difference (d) = 2 seconds
AP = 51, 49, 47 ...... .
(ii) Goal = 31 second
n = number of days
∴ an = 31
a + (n – 1)d = 31
51 + (n – 1)(– 2) = 31
51 – 2n + 2 = 31
– 2n = 31 – 53
– 2n = – 22
n = 11.
|
303 docs|7 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper- Term II (2021-22) - 4 - CBSE Sample Papers For Class 10
| 1. What is the duration of Class-X Mathematics exam and what is the maximum marks? |  |
| 2. How is the Class-X Mathematics exam divided into sections? |  |
| 3. What is the purpose of Section A in the Class-X Mathematics exam? |  |
| 4. What is the significance of Section B in the Class-X Mathematics exam? |  |
| 5. What is the content of Section C in the Class-X Mathematics exam? |  |

|
Explore Courses for Class 10 exam
|

|




















 ...(ii)
...(ii)



























