Class 10 Mathematics: CBSE Sample Question Paper- Term II (2021-22) - 3 | CBSE Sample Papers For Class 10 PDF Download
| Table of contents |

|
| Class-X |

|
| Time: 120 |

|
| Minutes |

|
| M.M: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-X
Time: 120
Minutes
M.M: 40
General Instructions:
Read the following instructions very carefully and strictly follow them:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section - A
Q.1. Solve the following quadratic equation for x:
4x2 – 4a2x + (a4 – b4) = 0
OR
Find the value(s) of k for which the quadratic equation x2 + 2√2 kx + 18 = 0 has equal roots.
Given, 4x2 – 4a2x + (a4 – b4) = 0
Comparing with Ax2 + Bx + C = 0, we get
Here, A = 4, B = –4a2 and C = (a4 – b4)
Since, x =
Then,
⇒
⇒
⇒
⇒
∴
OR
Since, x2 + 2√2 kx + 1 8 = 0 has equal roots then discriminant, D = 0
Comparing x2 + 2√2 kx + 18 = 0 with ax2 + bx + c = 0,
Now, a = 1, b = 2 √2 k and c = 18
D = 0
⇒ b2 = 4ac
(2√2k)2 = 4 × 1 × 18
4 × 2 × k2 = 72
k2 = 72/8
k2 = 9 ⇒ k = √9
k = ± 3.
Q.2. Show that (a – b)2, (a2 + b2) and (a + b)2 are in A.P. .
OR
Which term of the A.P. 3, 15, 27, 39,... will be 120 more than its 21st term?
Given, (a – b)2, (a2 + b2) and (a + b)2
Common difference,
d1 = (a2 + b2) – (a – b)2
= a2 + b2 – (a2 + b2 – 2ab)
= a2 + b2 – a2 – b2 + 2ab
= 2ab
and d2 = (a + b)2 – (a2 + b2)
= a2 + b2 +2ab – a2 – b2
= 2ab
Since, d1 = d2
Hence, (a – b)2, (a2 + b2) and (a + b)2 are in an A.P.
OR
an = a21 + 120
= (3 + 20 × 12) + 120 = 363
∴ 363 = 3 + (n – 1) × 12
⇒ n = 31
or 31st term is 120 more than a21.
Detailed Solution:
Given A.P. is: 3, 15, 27, 39
Here, first term, a = 3 and common difference, d = 12
Now, 21st term of A.P. is t21 = a + (21 – 1) d
∴ t21 = 3 +20 × 12 = 243
Therefore, 21st term is 243
We need to calculate term which is 120 more than 21st term
i.e., it should be 243 + 120 = 363
Therefore, tn = 363∴ tn = a + (n – 1)d
⇒ 363 = 3 + (n – 1)12
⇒ 360 = 12(n – 1)
⇒ n – 1 = 30
⇒ n = 31
So, 31st term is 120 more than 21st term.
Q.3. In the figure, quadrilateral ABCD is circumscribing a circle with centre O and AD ⊥ AB. If radius of incircle is 10 cm, then find the value of x.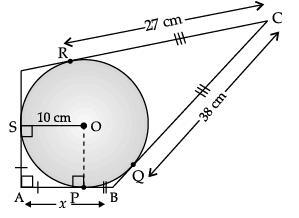
∠A = ∠OPA = ∠OSA = 90°
Hence, ∠SOP = 90°
Also, AP = AS
Hence, OSAP is a square.
AP = AS = 10 cm
CR = CQ = 27 cm
BQ = BC – CQ
= 38 – 27 = 11 cm
BP = BQ = 11 cm
x = AB = AP + BP
= 10 + 11 = 21 cm
Detailed Solution:
With O as centre, draw a perpendicular OP on AB.
Now, in quadrilateral APOS,∠SAP = 90° (Given)
∠APO = 90° (By construction)
and ∠ASO = 90° (Angle between tangent and radius)
Finally ∠SOP = 360° – (90° + 90° + 90°)
= 90°
AP = AS (Tangents from external point A)
∴ OSAP is a square.
AP = A S = SO = 10 cm
∵ CR = CQ (Tangents from external point C)
∴ CR = CQ = 27 cm
But BC = 38 cm (Given)
∴ BQ = BC – CQ = (38 – 27) cm
BQ = 11 cm
BP = BQ (Tangent from external point B)
∴ BP = 11 cm
So, x = AB = AP + PB
= (10 + 11) cm = 21 cm
Hence, the value of x is 21 cm.
Q.4. Solve for x:
x2 + 5x – (a2 + a – 6) = 0
Given,
x2 + 5x – (a2 + a – 6) = 0
Then,
Thus, x= a – 2 or x = – (a + 3)
Detailed Solution:
x2 + 5x – (a2 + a – 6) = 0
⇒ x2 + 5x – (a2 + 3a – 2a – 6) = 0
⇒ x2 + 5x – [a(a + 3) – 2(a + 3)] = 0
⇒ x2 + 5x – (a + 3)(a – 2) = 0
⇒ x2 + [(a + 3) – (a – 2)]x – (a + 3)(a – 2) = 0
⇒ x2 + (a + 3)x – (a – 2)x – (a + 3)(a – 2) = 0
⇒ x[x + (a + 3)] – (a – 2) [x + (a + 3)] = 0
⇒ [x + (a + 3)] [x – (a – 2)] = 0
⇒ x = – (a + 3) or x = a – 2
Hence, roots of given equation are – (a + 3) and a – 2.
Q.5. The (3/4)th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
Radius of conical vessel = 5 cm
and its height = 24 cm
Volume of cone vessel = (1/3)πR2H
= (1/3) x π x 5 x 5 x 24 = 200π cm3.
Internal radius of cylindrical vessel = 10 cm
Let the height of emptied water be h.
∴ Volume of water in cylinder = (3/4) x Volume of cone
⇒ πr2h = (3/4) x Volume of cone
⇒ π × 10 × 10 × h = 150π
⇒ h = 1.5 cm
Hence the height of water = 1.5 cm
Q.6. The mean of the following frequency distribution is 25. Find the value of p.
⇒
⇒ 650 + 25p = 570 + 45p
⇒ 650 – 570 = 45p – 25p
∴ p = 4
Section - B
Q.7. Find the arithmetic mean of the following frequency distribution :
Arithmetic Mean
= 1002.5/35 = 28.6 (Approx)
Q.8. Draw a line segment AB of length 9 cm. With A and B as centres, draw circles of radius 5 cm and 3 cm respectively. Construct tangents to each circle from the centre of the other circle.
Detailed Solution:
Steps of Construction :
(i) Draw a line segment AB of 9 cm.
(ii) Taking A and B as centres draw two circles of radii 5 cm and 3 cm respectively.
(iii) Perpendicular bisect the line AB. Let midpoint of AB be C.
(iv) Taking C as centre draw a circle of radius AC which intersects the two circles at point P, Q, R and S.
(v) Join B P, BQ, AS and AR.
BP, BQ and AR, AS are the required tangents.
Q.9. The median of the following data is 525. Find the values of x and y, if total frequency is 100.
Also, 76 + x + y = 100
⇒ x + y = 100 – 76 = 24 ...(i)
Given, Median = 525, which lies between class 500 – 600.
⇒ Median class = 500 – 600
Now, Median =
⇒ 525 = 500 +
⇒ 25 = (50 – 36 – x) 5
⇒ 14 – x = 25/5 = 5
⇒ x = 14 – 5 = 9
Putting the value of x in eq. (i), we get
y = 24 – 9 = 15
Hence, x = 9 and y = 15.
Q.10. The two palm trees are of equal heights and are standing opposite to each other on either side of the river, which is 80 m wide. From a point O between them on the river the angles of elevation of the top of the trees are 60° and 30°, respectively. Find the height of the trees and the distances of the point O from the trees. (use√3 = 1.73)
OR
The ratio of the length of a vertical rod and the length of its shadow is 1 : √3 . Find the angle of elevation of the Sun at that moment ?
Let BD = width of river = 80 m
AB = CD = height of both trees = h
BO = x
OD = 80 – x
In ΔABO, ∠B = 90°
tan 60° = h/x
√3 = h/x
h = √3x ....(i)
In ΔCDO, ∠D = 90°
tan 30° = h/(80 - x)
1/√3 = h/(80-x) ......(ii)
Solving (i) and (ii), we get
x = 20 m
h = √3x [From eqn. (i)]
= 1.73 × 20 m
= 34.6 m
The height of the trees = h = 34.6 m
BO = x = 20 m
DO = 80 – x
= 80 – 20 = 60 m
∴ The distances of the point O from the trees are 20 m and 60 m respectively.
OR
Let AB be a vertical rod and BC be its shadow.
From the figure, ∠ACB = θ.
In ΔABC, ∠B = 90°
Section - C
Q.11. The given figure is a decorative block, made up of two solids : a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has a diameter of 3.5 cm. Find the total surface area of the block. [Use π= 22/7].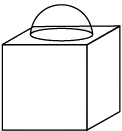
Surface area of block
= 216 - (22/7) x (3.5/2) x (3.5/2) + 2 x (22/7) x (3.5/2) x (3.5/2)
= 225.625 cm2.
Detailed Solution:
Given, Side of cube = 6 cm
Diameter of hemisphere = 3.5 cm
Radius of hemisphere = 3.5/2
Total surface area of cube = 6a2
= 6 × (6)2 = 216 cm2
Total surface area of solid = TSA of cube – Area of circle + CSA of hemisphere.
Q.12. In given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.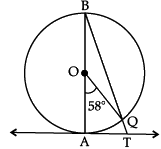 OR
OR
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
∠AOQ = 58° (Given)
∠ABQ = 1/2 ∠AOQ
(Angle on the circumference of the circle by the same arc)
= 1/2 x 58°
= 29°∠BAT = 90° (∵ OA ⊥ AT)
∴ ∠ATQ = 90° – 29° = 61°
OR
Given: A circle with centre O is inscribed in a quadrilateral ABCD.
In ∆AEO and ∆AFO,
OE = OF (radii of circle)
∠OEA = ∠OFA = 90° (radius is ⊥r to tangent)The point of contact is perpendicular to the tangent.
OA = OA (common side)
∆AEO ≅ ∆AFO (R.H.S. congruency)
∠7 = ∠8 (By cpct) ...(i)
Similarly,
∠1 = ∠2 ...(ii)
∠3 = ∠4 ...(iii)
∠5 = ∠6 ...(iv)
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360° (angle around a point is 360°)
2 ∠1 + 2 ∠8 + 2 ∠4 + 2∠5 = 360°
∠1 + ∠8 + ∠4 + ∠5 = 180°
(∠1 + ∠8) + (∠4 + ∠5) = 180°
∠AOB + ∠COD = 180° Hence Proved.
Case Study-1
Q.13. A circus artist is climbing from the ground along a rope stretched from the top of a vertical pole and tied at the ground. The height of the pole is 12 m and the angle made by the rope with ground level is 30°.
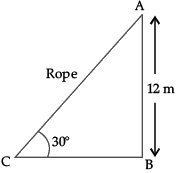
Give answer of the following questions:
(i) Find the distance covered by the artist in climbing the top of the pole.
(ii) Calculate the length of BC.
(i) Clearly, distance covered by the artist is equal to the length of the rope AC.
Let AB be the vertical pole of height 12 m.
It is given that ∠ACB = 30°
Thus, in right-angled triangle ABC,
sin 30° = AB/AC
⇒ 1/2 = 12/AC
∴ AC = 24 m.
(ii) In ΔABC, ∠B = 90°
tan 30° = AB/BC
⇒ 1/√3 = 12/BC
⇒ BC = 12√3 m.
Case Study- 2
Q.14. Jaspal Singh takes a loan from a bank for his car.
Jaspal Singh repays his total loan of ₹ 118000 by paying every month starting with the first installment of ₹ 1000. If he increases the installment by ₹ 100 every month.

(i) Calculate the amount paid by him in 25th installment.
(ii) Calculate the amount paid by him in 30th installment.
(i) The amount paid by him in 25th installment is:
T25 = a + 24d
= 1000 + 24 × 100
= 1000 + 2400 = ₹ 3400.
(ii) The amount paid by him in 30th installment,
T30 = a + 29d
= 1000 + 29 × 100
= 1000 + 2900 = ₹ 3900.
|
303 docs|7 tests
|

|
Explore Courses for Class 10 exam
|

|
















 Detailed Solution:
Detailed Solution:



























