Class 10 Mathematics: CBSE Sample Question Paper- Term I (2021-22) - 4 | CBSE Sample Papers For Class 10 PDF Download
Class-X
Time: 90 Minutes
M.M: 40
General Instructions:
- The question paper contains three parts A, B and C.
- Section A consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section B consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
Section - A
Q.1: The ratio of LCM and HCF of the least composite and the least prime numbers is
(a) 1:2
(b) 2:1
(c) 1:1
(d) 1:3
Correct Answer is Option (b)
Least composite number is 4 and the least prime number is 2.
LCM(4,2) : HCF(4,2) = 4:2 = 2:1
Q.2: The value of k for which the lines 5x+7y=3 and 15x + 21y = k coincide is
(a) 9
(b) 5
(c) 7
(d) 18
Correct Answer is Option (a)
For lines to coincide:
Q.3: A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is
(a) 350m
(b) 250m
(c) 300m
(d) 225m
Correct Answer is Option (b)
By Pythagoras theorem The required distance =
So the distance of the girl from the starting point is 250m.
Q.4: The lengths of the diagonals of a rhombus are 24cm and 32cm, then the length of the altitude of the rhombus is
(a) 12 cm
(b) 12.8 cm
(c) 19 cm
(d) 19.2 cm
Correct Answer is Option (d)
Area of the Rhombus = 1/2 d1d2
= 1/2 ×24×32 = 384 cm2
Using Pythagoras theorem
side2 = (1/2 d1)2 + (1/2 d2)2= 122 + 162 = 144 + 256 = 400
Side = 20cm
Area of the Rhombus = base x altitude
384 = 20 x altitude
So altitude = 384/20 = 19.2 cm
Q.5: Two fair coins are tossed. What is the probability of getting at the most one head?
(a) 3/4
(b) 1/4
(c) 1/2
(d) 3/8
Correct Answer is Option (a)
Possible outcomes are (HH), (HT), (TH), (TT)
Favorable outcomes(at the most one head) are (HT), (TH), (TT) So probability of getting at the most one head = 3/4
Q.6: ΔABC~ΔPQR. If AM and PN are altitudes of ΔABC and ΔPQR respectively and AB2 : PQ2 = 4 : 9, then AM:PN =
(a) 16:81
(b) 4:9
(c) 3:2
(d) 2:3
Correct Answer is Option (d)
Ratio of altitudes = Ratio of sides
For similar triangles So AM:PN = AB:PQ = 2:3
Q.7: If 2sin2β – cos2β = 2, then β is
(a) 0°
(b) 90°
(c) 45°
(d) 30°
Correct Answer is Option (b)
2sin2β – cos2β = 2
Then 2 sin2β – (1– sin2β) = 2
3 sin2β =3 or sin2β =1
β is 90°
Q.8: Prime factors of the denominator of a rational number with the decimal expansion 44.123 are
(a) 2,3
(b) 2,3,5
(c) 2,5
(d) 3,5
Correct Answer is Option (c)
Since it has a terminating decimal expansion, So prime factors of the denominator will be 2,5.
Q.9: The lines x = a and y = b, are
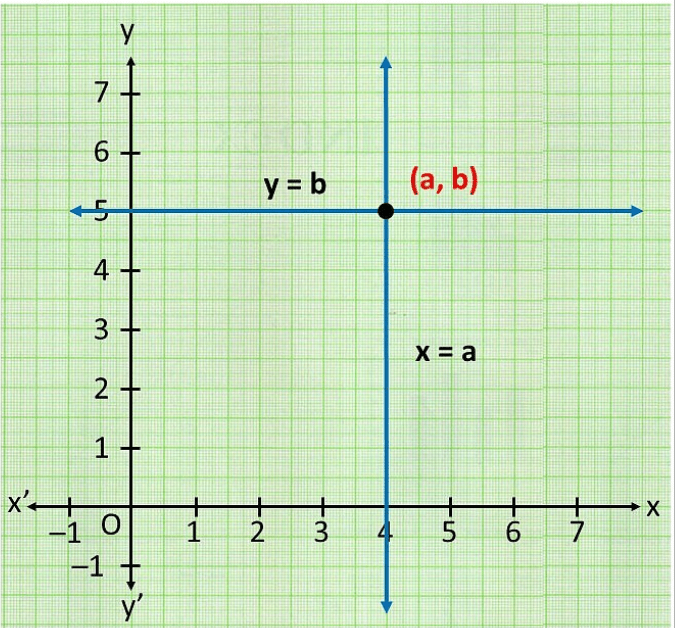 (a) intersecting
(a) intersecting
(b) parallel
(c) overlapping
(d) None of these
Correct Answer is Option (a)
Lines x = a is a line parallel to y axis and y=b is a line parallel to x axis. So they will intersect.
Q.10: The distance of point A(-5, 6) from the origin is
(a) 11 units
(b) 61 units
(c) √11 units
(d) √61 units
Correct Answer is Option (d)
Distance of point A (–5,6) from the origin (0,0) is
Q.11: If a² = 23/25, then a is
(a) rational
(b) irrational
(c) whole number
(d) integer
Correct Answer is Option (b)
a² = 23/25, then a = √23/5, which is irrational
Q.12: If LCM (x, 18) = 36 and HCF (x, 18) = 2, then x is
(a) 2
(b) 3
(c) 4
(d) 5
Correct Answer is Option (c)
LCM × HCF = Product of two numbers
36 × 2 = 18 × x
x = 4
Q.13: In ΔABC right angled at B, if tan A = √3 , then cos A cos C- sin A sin C =
(a) –1
(b) 0
(c) 1
(d) 3 /2
Correct Answer is Option (b)
tan A = √3 = tan 60° so √A=60°
Hence √C=30°.So cos A cos C- sin A sin C = (1/2)x (√3/2) – (3/2) x (1/2) = 0
Q.14: If the angles of ΔABC are in ratio 1:1:2, respectively (the largest angle being angle C), then the value of sec A/cosec B - tan A/cot B is
(a) 0
(b) 1/2
(c) 1
(d) √3/2
Correct Answer is Option (a)
1x +1x +2x =180°, x = 45°.
∠A, ∠B and ∠C are 45°, 45° and 90° resp.
Q.15: The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is
(a) 22
(b) 24
(c) 75
(d) 40
Correct Answer is Option (d)
Number of revolutions =
Q.16: ΔABC is such that AB = 3 cm, BC= 2cm, CA = 2.5 cm. If ΔABC ~ ΔDEF and EF = 4cm, then perimeter of ΔDEF is
(a) 7.5 cm
(b) 15 cm
(c) 22.5 cm
(d) 30 cm
Correct Answer is Option (b)
So perimeter of ∆DEF = 15 cm
Q.17: In the figure, if DE || BC, AD = 3cm, BD = 4cm and BC = 14cm, then DE equals
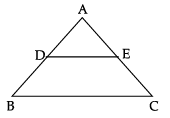
(a) 7cm
(b) 6cm
(c) 4cm
(d) 3cm
Correct Answer is Option (b)
Since DE || BC, ΔABC ~ ΔADE ( By AA rule of similarity)
So, DE = 6 cm
Q.18: If 4 tanβ = 3, then 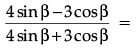
(a) 0
(b) 1/3
(c) 2/3
(d) 3/4
Correct Answer is Option (a)
Dividing both numerator and denominator by cosβ,
Q.19: One equation of a pair of dependent linear equations is – 5x + 7y = 2. The second equation can be 1
(a) 10x + 14y + 4 = 0
(b) – 10x – 14y + 4 = 0
(c) – 10x + 14y + 4 = 0
(d) 10x – 14y = – 4
Correct Answer is Option (d)
–2(–5x + 7y = 2) gives 10x – 14y = –4.
Now,
Q.20: A letter of English alphabets is chosen at random. What is the probability that it is a letter of the word ‘MATHEMATICS’?
(a) 4/13
(b) 9/26
(c) 5/13
(d) 11/26
Correct Answer is Option (a)
Number of Possible outcomes are 26 Favourable outcomes are M, A, T, H, E, I, C, S probability = 8/26 = 4/13
Section - B
Q.21: The value of k for which the system of equations kx + 5y = k – 4 and 10x + ky = k will have infinite many solutions is:
(a) – 3
(b) ± 5√2
(c) ± 6
(d) 4
Correct Answer is Option (a)
Here,
The system will have infinite solutions if
Q.22: If three vertices of a triangle are (1, 4), (5, 6) and (4, 7), then its centroid is:
(a) (3, 6)
(b) (10/3), 17/3)
(c) (11/3), 17/3)
(d) (10/3), 6)
Correct Answer is Option (b)
Centroid of a triangle
Q.23: If the probability of an event is p, then the probability of its complementary event will be:
(a) p – 1
(b) p
(c) 1 – p
(d) 1 - 1/p
Correct Answer is Option (a)
Probability of an event + Probability of its complementary event = 1
∴ p + Probability of complement = 1 Probability of complement = 1 – p
Q.24: If sin B = 1/2, then the value of 3 cos B – 4 cos3 B is:
(a) 1
(b) 0
(c) 2
(d) 3
Correct Answer is Option (b)
Given,
Q.25: The area of the corresponding major segment of a circle of radius 21 cm and the central angle 60° is: A
(a) 1108 cm2
(b) 1114 cm2
(c) 1128 cm2
(d) 1155 cm2
Correct Answer is Option (a)
Here, r = 21 cm and q = 60°
Then, the area of major sector = πr2 –
= 1155 cm2
Q.26: In the given figure, ABCD is rectangle. The value of x is:
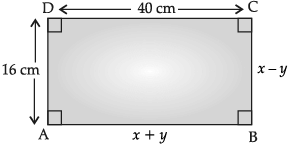
(a) 28 cm
(b) 26 cm
(c) 25 cm
(d) 24 cm
Correct Answer is Option (a)
Since ABCD is a rectangle, AB = CD
i.e., x + y = 40 ...(i)
and BC = AD
i.e., x – y = 16 ...(ii)
On adding eq. (i) and (ii), we get 2x = 56⇒ x = 28 cm.
Q.27: The line x + 3y = 6 meets the y-axis:
(a) (0, 1)
(b) (0, 2)
(c) (0, 3)
(d) (1, 0)
Correct Answer is Option (a)
Given line is:
x + 3y = 6
Taking the point (0, 2) i.e., x = 0 and y = 2
Putting the value of x and y in LHS.
x + 3y = 0 + 3 × 2 = 6, which is equal to RHS.
Q.28: The coordinates of the point which divides the line segment joining the points (7, 4) and (– 5, 3) in the ratio 3 : 4 internally is:
(a) (13/7, 25/7)
(b) (2, 24/7)
(c) (3, 25/7)
(d) (4, 25/7)
Correct Answer is Option (a)
Let p(x, y) be the required point, then
Q.29: The point (– 3, p) divides the line segment joining the points (– 4, – 3) and (– 1, 4) in the ratio is:
(a) 2 : 1
(b) 3 : 1
(c) 1 : 2
(d) 1 : 3
Correct Answer is Option (c)
Let the ratio be k : 1, then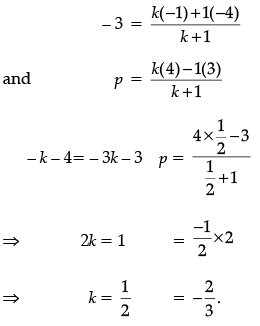
The Ratio is 1/2 : 1 = 1: 2
Q.30: It is given that ΔABC ~ ΔPQR with BC/QR = 25, then  is:
is:
(a) 25/4
(b) 4/25
(c) 29/25
(d) 25/29
Correct Answer is Option (a)

Q.31: If ABC is a right angled triangle at C and AC = √3 BC , then AB is equal to:
(a) BC
(b) 3BC
(c) 2BC
(d) 4BC
Correct Answer is Option (c)
In ΔABC, AB2 = AC2 + BC2 (Using Pythagoras theorem)
= ( 3BC)2 + BC2[∵ AC = √3BC ]
= 3BC2 + BC2
AB2 = 4BC2
Hence, AB = 2BC.
Q.32: If 16 cot x = 12, then the value of sincos sincos  is :
is :
(a) 2/7
(b) 3/7
(c) 4/7
(d) 1/7
Correct Answer is Option (d)
∵ 16 cot x = 12
⇒ cot x = 12/16 = 3/4
Then, tan x = 1/cot x= 4/3.
Q.33: If 16 cot x = 12. then the value of 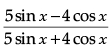
(a) 3/7
(b) 5/4
(c) 1/4
(d) 7/4
Correct Answer is Option (c)
According to question 32,
Q.34: If tan A = 5/12, then the value of (sin A + cos A) sec A is :
(a) 17/12
(b) 19/12
(c) 1/12
(d) 3/4
Correct Answer is Option (a)
(sin A + cos A) . sec A
Q.35: If radius of a circle is 6 cm and of angle 30° at the centre, then the length of the arc is:
(a) 31.4 cm
(b) 3.14 cm
(c) 003.14 cm
(d) 0.314 cm
Correct Answer is Option (b)
Here, r = 6 cm and θ = 30°.
The length of arc
Q.36: The minute hand of a clock is 20 cm long. So the angle described by the minute hand in 20 minutes is:
(a) 30°
(b) 60°
(c) 90°
(d) 120°
Correct Answer is Option (d)
Angle described by the minute hand in 20 minutes
= 360°/60°x20
= 120°
Q.37: A bag contains 9 red, 6 green and 5 white balls, one ball is drawn at random from the bag, then the probability of getting not a white ball is:
(a) 3/4
(b) 1/4
(c) 1/2
(d) 1/3
Correct Answer is Option (a)
Total no. of balls = 9 + 6 + 5
= 20
i.e., n(S) = 20
In case of assertion,
No. of white balls = 5P (white ball) = 5/20 = 1/4
∴ P (not a white ball)
= 1 - P(white ball)
Q.38: From the numbers 3, 4, 4, 6, 6, 6, 8, 8, 8, 8, one number is selected at random, then the probability of the selected number 4 is:
(a) 2/5
(b) 3/5
(c) 1/5
(d) 1/4
Correct Answer is Option (c)
Total numbers = 10
i.e., n(S) = 10
In case of assertion,
The numbers of four = 2
∴ P (selected no. 4) = 2/10= 1/5.
Q.39: Rahul draws a quadrilateral having points A(– 2, – 1), B(1, 0), C(4, 3) and D(1, 2) are the vertices of a quadrilateral. Then, he tries to find the mid-point of AC of that quadrilateral. What is mid-point of AC.
(a) (2, –1)
(b) (1, 1)
(c) (–1, 2)
(d) (–2, 1)
Correct Answer is Option (b)
Mid-point of AC =
= (1, 1)
Q.40: If cot θ = 1/√3, then the value of 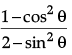 is:
is:
(a) 3/5
(b) 4/5
(c) 1/5
(d) 9/5
Correct Answer is Option (a)
Section - C
Q.41 to 45 are based on Case Study-1
For a linear polynomial kx + c, k ≠ 0, the graph of y = kx + c is a straight line which intersects the X-axis at exactly one point, namely, (-c/k, 0), Therefore, the linear polynomial kx + c, k ≠ 0, has exactly one zero, namely, the X-coordinate of the point where the graph of y = kx + c intersects the X-axis.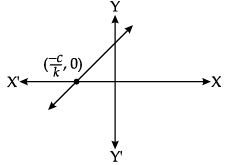
Q.41: If a linear polynomial is 2x + 3, then the zero of 2x + 3 is:
(a) 3/2
(b) − 3/2
(c) 2/3
(d) − 2/3
Correct Answer is Option (b)
Given, polynomial = 2x + 3
Let p(x) = 2x + 3
For a zero of p(x),
2x + 3 = 0
⇒ 2x = – 3
⇒ x = − 3/2.
Q.42: The graph of y = p(x) is given in figure below for some polynomial p(x). The number of zero/zeroes of p (x) is/are: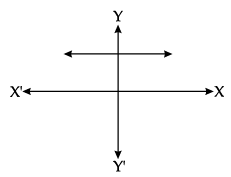
(a) 1
(b) 2
(c) 3
(d) 0
Correct Answer is Option (d)
Since the graph does not intersect the X-axis, therefore it has no zero.
Q.43: If α and β are the zeroes of the quadratic polynomial x2 – 5x + k such that a – b = 1, then the value of k is:
(a) 4
(b) 5
(c) 6
(d) 3
Correct Answer is Option (d)
∵ p(x) = x2 – 5x + k
Then
Q.44: If a and b are the zeroes of the quadratic polynomial p(x) = 4x2 +5x +1, then the product of zeroes is:
(a) – 1
(b) 1/4
(c) – 2
(d) − 5/4
Correct Answer is Option (b)
We have, p(x) = 4x2 + 5x + 1
∴ αβ = c/a = 1/4.
Q.45: If the product of the zeroes of the quadratic polynomial p(x) = ax2 – 6x – 6 is 4, then the value of a is:
(a) − 3/2
(b) 3/2
(c) 2/3
(d) − 2/3
Correct Answer is Option (a)
We have, p(x) = ax2 – 6x – 6
Let α and β be the zeroes of the given polynomial, then
Q.46 to 50 are based on Case Study - 2
The coordinates of the vertices of DPQR are P(5, 4), Q(11, 8) and R(3, 6). If S and T are the mid points of PQ and PR respectively, then give the answer of following questions: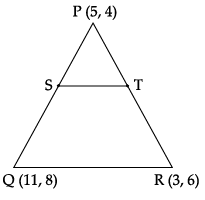
Q.46: The coordinates of the point S is:
(a) (8, 6)
(b) (4, 3)
(c) (9, 6)
(d) (5, 3)
Correct Answer is Option (a)
Coordinates of the point
Q.47: The coordinates of the point T is:
(a) (5, 6)
(b) (9, 6)
(c) (7, 3)
(d) (4, 5)
Correct Answer is Option (d)
Coordinates of the point
Q.48: The length of ST is:
(a) 10 units
(b) √17 units
(c) √15 units
(d) 6 units
Correct Answer is Option (b)
Length of ST =
Q.49: The length of QR is:
(a) 6 units
(b) √67 units
(c) √68 units
(d) 5 units
Correct Answer is Option (c)
Q.50: If X is the mid point of QR, then the coordinates of X is:
(a) (7, 7)
(b) (4, 3)
(c) (8, 6)
(d) (5, 6)
Correct Answer is Option (a)
|
303 docs|7 tests
|

|
Explore Courses for Class 10 exam
|

|



 So the distance of the girl from the starting point is 250m.
So the distance of the girl from the starting point is 250m.


 So perimeter of ∆DEF = 15 cm
So perimeter of ∆DEF = 15 cm So, DE = 6 cm
So, DE = 6 cm













































