Class 10 Maths Chapter 1 Case Based Questions - Real Numbers
| Table of contents |

|
| Case Study – 1 |

|
| Case Study – 2 |

|
| Case Study – 3 |

|
| Case Study – 4 |

|
| Case Study – 5 |

|
Case Study – 1
We all know that morning walk is good for health. In a morning walk, three friends Anjali, Sofia, and Angelina step of together. There steps measure 80 cm, 85 cm, and 90 cm. respectively.
Q1: What is the minimum distance each should walk so that they can cover the distance in complete steps?
(a) 120 m 40 cm
(b) 122 m 40 cm
(c) 12 m 4 cm
(d) None of these
Ans: (b)
Explanation: The process of solving this problem involves finding the least common multiple (LCM) of the three given measurements. The LCM of a set of numbers is the smallest number that is a multiple of each of the numbers in the set.
Here are the steps to find the LCM of 80 cm, 85 cm, and 90 cm:
Step 1: Prime factorization
The first step is to find the prime factors of each number.
- For 80, the prime factors are 2, 2, 2, 2, and 5 (or 2⁴ х 5)
- For 85, the prime factors are 5 and 17
- For 90, the prime factors are 2, 3, 3, and 5 (or 2 х 3² х 5)
Step 2: Find the LCM
Now, we find the LCM by taking the highest power of each prime factor from all the numbers.
- The highest power of 2 is 2⁴ from 80
- The highest power of 3 is 3² from 90
- The highest power of 5 is 5 from 80 or 90
- The highest power of 17 is 17 from 85
So, the LCM is 2⁴ х 3² х 5 х 17 = 12240
Step 3: Convert cm to m
Finally, we convert the LCM from centimeters to meters. Since 1 meter is 100 cm, we divide 12240 by 100 to get 122.4 meters, which can also be written as 122 meters and 40 cm.
Therefore, the minimum distance each should walk so that they can cover the distance in complete steps is 122 meters and 40 cm. This corresponds to option (b).
Q2: What is the minimum number of steps taken by any of the three friends, when they meet again?
(a) 120
(b) 125
(c) 130
(d) 136
Ans: (d)
Explanation: To solve this problem, we need to find the least common multiple (LCM) of the step sizes of the three friends: 80 cm, 85 cm, and 90 cm. The LCM will give us the smallest distance that all three friends can walk together, taking whole steps.
Here is the step-by-step process:
Step 1: Prime Factorization
We start by breaking down each number into its prime factors.
- 80 = 2 x 2 x 2 x 2 x 5 = 2⁴ x 5
- 85 = 5 x 17
- 90 = 2 x 3 x 3 x 5 = 2 x 3² x 5
Step 2: Find the LCM
The LCM is found by taking the highest power of all the prime numbers that appear in the prime factorization of any of the numbers.
LCM = 2⁴ x 3² x 5 x 17 = 12240 cm
This means that the three friends will meet again after walking a distance of 12240 cm.
Step 3: Determine the Minimum Steps
Among the three friends, Angelina has the longest step size (90 cm). Therefore, she will take the smallest number of steps to cover the distance of 12240 cm.
Number of steps taken by Angelina = Total distance / Step size
= 12240 cm / 90 cm
= 136 steps
Hence, the correct answer is (d) 136 steps.
Q3: The HCF of 80, 85, and 90 is
(a) 5
(b) 10
(c) 12
(d) 18
Ans: (a)
Explanation: The Highest Common Factor (HCF) of a set of numbers is the largest number that divides evenly into all the numbers in the set. In this case, we are looking for the HCF of 80, 85, and 90.
The first step is to determine the prime factors of each of the numbers. Prime factors are the factors of a number that are prime numbers.
1. For 80, the prime factors are 2 and 5. We obtain this by dividing 80 by the smallest prime number (2) as many times as possible until we are left with a prime number. This gives us 2 x 2 x 2 x 2 x 5 = 2⁴ x 5.
2. For 85, the prime factors are 5 and 17. We obtain this by dividing 85 by the smallest prime number (2) as many times as possible until we are left with a prime number. This gives us 5 x 17.
3. For 90, the prime factors are 2, 3, and 5. We obtain this by dividing 90 by the smallest prime number (2) as many times as possible, then doing the same with the next smallest prime number (3) until we are left with a prime number. This gives us 2 x 3 x 3 x 5 = 2 x 3² x 5.
Now that we have the prime factors of each number, we can determine the HCF by finding the largest number that is a factor of all three numbers. In this case, the only common factor among 80, 85, and 90 is 5.
Therefore, the HCF of 80, 85, and 90 is 5, which corresponds to answer choice (a).
Q4: The product of HCF and LCM of 80, 85, and 90 is
(a) 60400
(b) 61000
(c) 61200
(d) 65500
Ans: (c)
Explanation: The problem requires us to find the product of the Highest Common Factor (HCF) and the Least Common Multiple (LCM) of the numbers 80, 85, and 90.
Step 1: To find the HCF and LCM, we first need to find the prime factors of the three numbers.
For 80, the prime factors are 2 x 2 x 2 x 2 x 5 (or 24 x 5).
For 85, the prime factors are 5 x 17.
For 90, the prime factors are 2 x 3 x 3 x 5 (or 2 x 32 x 5).
Step 2: To find the HCF, we look for common prime factors. The only common factor among all three numbers is 5. So, HCF = 5.
Step 3: For the LCM, we take the highest power of all the prime numbers in the factorization of each number. So, LCM = 22 x 32 x 5 x 17 = 12240.
Step 4: Finally, we need to find the product of the HCF and LCM. This is done by multiplying the HCF (5) with the LCM (12240), which gives us 61200.
So, the product of the HCF and LCM of 80, 85, and 90 is 61200. Therefore, the correct answer is option (C).
Q5: 90 can be expressed as a product of its primes as
(a) 2 х 3² х 5²
(b) 2 х 3³ х 5
(c) 2² х 3² х 5
(d) 2 х 3² х 5
Ans: (d)
Explanation: The question asks us to express 90 as a product of its prime factors. Prime factors are the factors of a number that are prime numbers. A prime number is a number that only has two factors: 1 and itself.
Here are the steps to find the prime factors of 90:
Step 1: Start by dividing the number 90 with the smallest prime number, which is 2. 90 is divisible by 2. So, divide 90 by 2. You get 45.
Step 2: Now, try dividing 45 by 2. It can't be divided evenly. So, we move to the next prime number, which is 3. 45 divided by 3 gives 15.
Step 3: Try dividing 15 by 3. It can't be divided evenly. So, we move to the next prime number, which is 5. 15 divided by 5 gives 3.
Step 4: Now, we are left with 3. 3 is a prime number itself, so we stop here.
So, the prime factors of 90 are 2, 3, 3, and 5. We can write this as 2 x 3² x 5, which matches option (d).
Therefore, the correct answer is (d).
Case Study – 2
A Mathematics Exhibition is being conducted in your School and one of your friends is making a model of a factor tree. He has some difficulty and asks for your help in completing a quiz for the audience.
Observe the following factor tree and answer the following: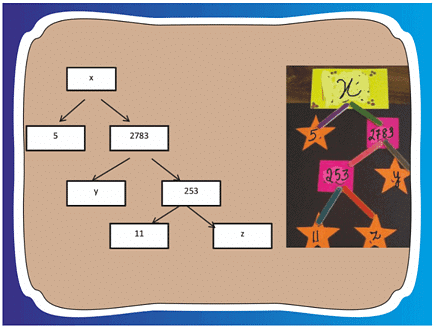
Q1: What will be the value of x?
(a) 15005
(b) 13915
(c) 56920
(d) 17429
Ans: (b)
Explanation: The factor tree is a method used to break down any given number into its prime factors. In this case, we don't have the factor tree visually, but the question suggests that 'x' can be obtained by multiplying the numbers 5 and 2783.
Step-by-step process:
Step 1: Identify the numbers given. Here, we have 5 and 2783.
Step 2: Multiply the given numbers. In this case, x = 5 * 2783
Step 3: Perform the multiplication. 5 * 2783 = 13915
So, by using these steps, we find that the value of 'x' is 13915. Therefore, the correct option is (b) 13915.
Q2: What will be the value of y?
(a) 23
(b) 22
(c) 11
(d) 19
Ans: (c)
Explanation: The given factor tree shows how a number is broken down into its prime factors. The number at the top of the tree is the original number and the numbers at the bottom are all prime factors.
In the question, we are not given the specific factor tree, but we are asked to find the value of 'y' given that Y = 2783/253.
To solve this, we need to perform the division operation:
2783 divided by 253 equals to 11.
Hence, the correct answer is option (c), i.e., y = 11.
Q3: What will be the value of z?
(a) 22
(b) 23
(c) 17
(d) 19
Ans: (b)
Explanation: The given factor tree is not explicitly provided here, but from the available solution, we can assume that the number 253 is divided by 11 on the factor tree to obtain the value of z.
The process for solving the problem is as follows:
Step 1: Identify the numbers given in the factor tree. Here, it's 253 divided by 11 to get 'z'.
Step 2: Divide the larger number (253) by the smaller number (11).
253 ÷ 11 = 23
So, z = 23.
Therefore, the correct answer is (b) 23.
In conclusion, a factor tree is a tool that breaks down any number into its prime factors. In this case, it helped to find the value of z by dividing 253 by 11.
Q4: According to Fundamental Theorem of Arithmetic 13915 is a
(a) Composite number
(b) Prime number
(c) Neither prime nor composite
(d) Even number
Ans: (a)
Explanation: The Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number, or can be represented as a unique product of prime numbers.
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. For example, the first six prime numbers are 2, 3, 5, 7, 11, and 13.
A composite number is a positive integer that has at least one positive divisor other than one or itself. In other words, a composite number is any positive integer greater than one that is not a prime number.
Now, let's consider the number 13915. We are given that 13915 can be written as the product of primes: 13915 = 5 х 11 х 11 х 23 = 5 х 11² х 23. Here, we can see that 13915 has more divisors than just 1 and itself (which are 5, 11 and 23). This means that 13915 is not a prime number.
Also, as 13915 can be expressed as a product of prime numbers, it is not a number that falls into the category of 'neither prime nor composite'.
As for being an even number, we know that an even number is any integer that can be divided by 2. In the case of 13915, it is not divisible by 2, so it is not an even number.
Therefore, by process of elimination and based on the definitions, we can conclude that 13915 is a composite number (option a).
Q5: The prime factorisation of 13915 is
(a) 5 х 11³ х 13²
(b) 5 х 11³ х 23²
(c) 5 х 11² х 23
(d) 5 х 11² х 13²
Ans: (c)
Explanation: The prime factorisation of a number is the representation of that number as the product of its prime factors.
Here's how you would calculate the prime factorisation of 13915 step-by-step:
- First, find the smallest prime number that divides 13915. This will be 5, because 13915 is not divisible by 2 (it's not an even number), nor by 3 (the sum of its digits is not divisible by 3). So, you can start with 5.
- Divide 13915 by 5, which gives you 2783.
- Now, repeat the process with 2783. The smallest prime number that divides 2783 is 11. Divide 2783 by 11 to get 253.
- Repeat the process with 253. It's not divisible by 2, 3, 5, or 7, but it is divisible by 11. Dividing by 11 gives you 23.
- 23 is a prime number itself, so that's the end of the process.
Therefore, the prime factorisation of 13915 is 5 x 11 x 11 x 23, or 5 x 11² x 23, which matches option (c).
Case Study – 3
Rohit Singh is a worker in a petrol pump. He along with the other co-workers, use to transfer petrol from tanker to storage. On Monday, there were two tankers containing 850 litres and 680 litres of petrol respectively.
Q1: What is the maximum capacity of a container which can measure the petrol of either tanker in exact number of time?
(a) 150 litres
(b) 160 litres
(c) 170 litres
(d) 180 litres
Ans: (c)
Explanation: The question is asking for the highest common factor (HCF) of 850 and 680. The HCF is the largest number that can evenly divide both numbers.
Step 1: Find the prime factors of both numbers.
Prime factors of 850 = 2 х 5 х 5 х 17 = 2 х 5² х 17
Prime factors of 680 = 2 х 2 х 2 х 5 х 17 = 2³ х 5 х 17
Step 2: Identify the common prime factors.
The common prime factors of 850 and 680 are 2, 5, and 17.
Step 3: Multiply the common prime factors to get the HCF.
HCF of 850 and 680 = 2 х 5 х 17 = 170
Therefore, the maximum capacity of a container that can measure the petrol of either tanker an exact number of times is 170 litres, which corresponds to option (c).
Q2: If the product of two positive integers is equal to the product of their HCF and LCM is true then, the LCM (850, 680) is
(a) 3100
(b) 3200
(c) 3300
(d) 3400
Ans: (d)
Explanation: The question is asking for the least common multiple (LCM) of 850 and 680. The LCM is the smallest number that is a multiple of both numbers.
Step 1: We already have the prime factors of both numbers from the previous question, and the HCF.
Prime factors of 850 = 2 х 5 х 5 х 17 = 2 х 5² х 17
Prime factors of 680 = 2 х 2 х 2 х 5 х 17 = 2³ х 5 х 17
HCF of 850 and 680 = 2 х 5 х 17 = 170
Step 2: Use the formula for finding the LCM when the HCF is known.
LCM (850, 680) = (850 х 680) / HCF
Step 3: Substitute the values into the formula.
LCM (850, 680) = (850 х 680) / 170 = 3400
Therefore, the LCM of 850 and 680 is 3400, which corresponds to option (d).
Q3: 680 can be expressed as a product of its primes as
(a) 2² х 5 х 17
(b) 2¹ х 5 х 17
(c) 2³ х 5 х 17
(d) 2³ х 5 х 17⁰
Ans: (c)
Explanation: To solve this problem, you need to understand what prime factorization is. Prime factorization is the process of breaking down a number into its smallest prime factors.
Let's try to factorize the number 680.
First, we need to find a prime number that can divide 680. The smallest prime number is 2, and it can divide 680, so we use it as our first factor.
680 ÷ 2 = 340
Now we continue the process with 340. Again, it can be divided by 2, so we use 2 as our next factor.
340 ÷ 2 = 170
We repeat the process with 170. It can be divided by 2, so we use 2 as our next factor.
170 ÷ 2 = 85
Now, 85 cannot be divided by 2, so we move to the next prime number, which is 3. However, 85 cannot be divided by 3 either. We continue this process until we find a prime number that can divide 85, which is 5.
85 ÷ 5 = 17
Finally, we have 17, which is a prime number itself, so our factorization process stops here.
Therefore, the prime factorization of 680 is 2 × 2 × 2 × 5 × 17, or in the exponential form, it is 2³ × 5 × 17. Hence, option (c) is correct.
Q4: 2 х 3 х 5 х 11 х 17 + 11 is a
(a) Prime number
(b) Composite number
(d) Neither prime nor composite
(d) None of the above
Ans: (b)
Explanation: The provided answer appears to be incorrect. The number 11 is indeed a prime number, not a composite number.
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In other words, if a number is prime, it can only be divided without a remainder by 1 and itself. The number 11 meets this criteria, as it can only be divided evenly by 1 and 11.
On the other hand, a composite number is a positive integer that has at least one positive divisor other than one or itself. In other words, it has more than two distinct divisors.
Here, the number 11 does not have more than two distinct divisors. Thus, the number 11 is a prime number. Therefore, the correct answer is (a) Prime number.
Q5: If p and q are positive integers such that p = a³b² and q = a²b³, where a, b are prime numbers, then the LCM (p, q) is
(a) ab
(b) a³b³
(c) a³b⁵
(d) a⁵b³
Ans: (b)
Explanation: To find the least common multiple (LCM) of two numbers, we need to consider the highest powers of all the factors in the numbers.
In this case, we are given that p = a³b² and q = a²b³, where a and b are prime numbers.
The factors of p are a and b, with a having a power of 3 and b having a power of 2.
The factors of q are also a and b, but here a has a power of 2 and b has a power of 3.
When finding the LCM, we need to take the highest powers of these common factors. So, we take a to the power of 3 (since 3 is higher than 2) and b to the power of 3 (since 3 is higher than 2).
Hence, the LCM of p and q is a³b³.
Therefore, the correct option is (b) a³b³.
Case Study – 4
A seminar is being conducted by an Educational Organisation, where the participants will be educators of different subjects. The number of participants in Hindi, English, and Mathematics are 60, 84, and 108 respectively.

Q1: In each room the same number of participants are to be seated and all of them being in the same subject, hence maximum number participants that can accommodated in each room are
(a) 14
(b) 12
(c) 16
(d) 18
Ans: (b)
Explanation: In order to find the maximum number of participants that can be accommodated in each room, we need to find the Highest Common Factor (HCF) of the number of participants in each subject.
The HCF of a set of numbers is the largest number that divides each of them without leaving a remainder. It can be found by listing all the factors of each number and finding the largest one that they have in common.
Here are the factors of each number:
- Factors of 60: 2 x 2 x 3 x 5 = 2² x 3 x 5
- Factors of 84: 2 x 2 x 3 x 7 = 2² x 3 x 7
- Factors of 108: 2 x 2 x 3 x 3 x 3 = 2² x 3³
The HCF of 60, 84, and 108 is 2² x 3 = 12. Therefore, the maximum number of participants that can be accommodated in each room is 12, which corresponds to the option (b).
Q2: What is the minimum number of rooms required during the event?
(a) 11
(b) 31
(c) 41
(d) 21
Ans: (d)
Explanation: The question requires us to calculate the minimum number of rooms required for the seminar. This can be done by finding the highest common factor (HCF) of the number of participants in each subject. The HCF tells us the maximum number of participants that can be accommodated in each room such that all rooms have the same number of participants.
Let's start by finding the prime factorization of the numbers.
For 60, the prime factors are 2, 2, 3, and 5 (2² х 3 х 5).
For 84, the prime factors are 2, 2, 3, and 7 (2² х 3 х 7).
For 108, the prime factors are 2, 2, 3, 3, and 3 (2² х 3³).
Now, the HCF is found by multiplying the lowest power of the common prime factors. In this case, the common prime factors are 2 and 3. The lowest power of 2 is 2 (as in 2²), and the lowest power of 3 is 1 (as in 3). So, the HCF is 2² х 3 = 12.
Now, to find the number of rooms required for each subject, we divide the number of participants by the HCF.
For Hindi, we need 60/12 = 5 rooms.
For English, we need 84/12 = 7 rooms.
For Mathematics, we need 108/12 = 9 rooms.
Adding these together, the total number of rooms required is 5 + 7 + 9 = 21 rooms.
Therefore, the answer is (d) 21.
Q3: The LCM of 60, 84, and 108 is
(a) 3780
(b) 3680
(c) 4780
(d) 4680
Ans: (a)
Explanation: The problem revolves around finding the Least Common Multiple (LCM) of three numbers: 60, 84, and 108.
To find the LCM of these numbers, we first need to find their prime factors.
Here's how:
- The prime factors of 60 are 2, 2, 3, and 5 (since 2*2*3*5 = 60). We can write it as 2² * 3 * 5.
- The prime factors of 84 are 2, 2, 3, and 7 (since 2*2*3*7 = 84). We can write it as 2² * 3 * 7.
- The prime factors of 108 are 2, 2, 3, 3, and 3 (since 2*2*3*3*3 = 108). We can write it as 2² * 3³.
Now, to find the LCM, we take the highest power of all the prime factors obtained from these numbers. If a prime factor is not present in one number but is present in another, we take the factor from the number where it is present.
- We have the factor 2 in all three numbers, and the highest power is 2². So, we take 2².
- We have the factor 3 in all three numbers, and the highest power is 3³. So, we take 3³.
- We have the factor 5 only in 60. So, we take 5.
- We have the factor 7 only in 84. So, we take 7.
Q4: The product of HCF and LCM of 60, 84, and 108 is
(a) 55360
(b) 35360
(c) 45500
(d) 45360
Ans: (d)
Explanation: The first step to solving this problem is understanding what HCF (Highest Common Factor) and LCM (Least Common Multiple) are.
The HCF is the highest number that can divide two or more numbers without leaving a remainder. The LCM is the smallest number that is a multiple of two or more numbers.
To find the HCF and LCM, we first need to find the prime factors of each number.
For 60, the prime factors are 2, 2, 3, and 5 (or 2², 3, 5).
For 84, the prime factors are 2, 2, 3, and 7 (or 2², 3, 7).
For 108, the prime factors are 2, 2, 3, 3, and 3 (or 2², 3³).
The HCF of these three numbers is found by taking the highest common factor of all three numbers, which is 2² (or 4) and 3. Multiplying these together gives us an HCF of 12.
The LCM is found by taking the highest power of all the prime factors present in the numbers. This gives us 2², 3³, 5, and 7. Multiplying these together gives us an LCM of 3780.
Finally, to find the product of the HCF and LCM, we multiply 12 and 3780 together, which gives us 45360. Hence, the correct answer is (d) 45360.
Q5: 108 can be expressed as a product of its primes as
(a) 2³ х 3²
(b) 2³ х 3³
(c) 2² х 3²
(d) 2² х 3³
Ans: (d)
Explanation: The process of finding the answer is called prime factorization.
Step 1: Start with the smallest prime number, which is 2. Check if 108 is divisible by 2. If it is, then write down 2 as a factor and divide 108 by 2.
Step 2: You get 54 as the quotient. Now, repeat the process with 54. Is it divisible by 2? Yes, it is. So, write down 2 as a factor again and divide 54 by 2.
Step 3: You now have a quotient of 27. Repeat the process. Is 27 divisible by 2? No, it's not. So, move on to the next prime number, which is 3.
Step 4: Is 27 divisible by 3? Yes, it is. So, write down 3 as a factor and divide 27 by 3.
Step 5: You get a quotient of 9. Repeat the process. Is 9 divisible by 3? Yes, it is. So, write down 3 as a factor again and divide 9 by 3.
Step 6: You now have a quotient of 3. Repeat the process. Is 3 divisible by 3? Yes, it is. So, write down 3 as a factor again and divide 3 by 3.
Step 7: You now have a quotient of 1. When you reach 1, you can stop the process.
Step 8: Now, count the number of times each prime number appears in your list of factors. You have two 2s and three 3s.
Step 9: Write down your answer as the product of the prime numbers, each raised to the power of its count. So, 108 = 2² х 3³.
That's how you get the answer (d) 2² х 3³.
Case Study – 5
To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section B of grade X. There are 32 students in section A and 36 students in section B.
Q1: What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?
(a)144
(b) 128
(c) 288
(d) 272
Ans: (c)
Explanation: The question requires finding the minimum number of books that can be equally distributed among the students of either section A or section B. This is essentially finding the least common multiple (LCM) of the number of students in both sections.
Step 1: Find the prime factors of both 32 and 36.
Prime factors of 32 are 2 x 2 x 2 x 2 x 2 = 2^5
Prime factors of 36 are 2 x 2 x 3 x 3 = 2^2 x 3^2
Step 2: Find the LCM of 32 and 36.
For finding the LCM, we take the highest power of each prime factor that appears in the factorization of either 32 or 36. Here, for 2, the highest power is 5 (from 32) and for 3, it is 2 (from 36).
So, LCM of 32 and 36 = 2^5 x 3^2 = 32 x 9 = 288.
Hence, you would need a minimum of 288 books so that they can be equally distributed among the students of either section A or section B. So, the correct option is (C).
Q2: If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32, 36) is
(a) 2
(b) 4
(c) 6
(d) 8
Ans: (b)
Explanation: To arrive at the solution, we need to understand two key concepts - Highest Common Factor (HCF) and Lowest Common Multiple (LCM). The HCF of two numbers is the highest number that can divide both of them without leaving a remainder. On the other hand, LCM of two numbers is the smallest number that can be divided by both of them without leaving a remainder.
Let's break down the problem into steps:
Step 1: Find the factors of the given numbers 32 and 36.
Factors of 32: 2*2*2*2*2 = 2⁵
Factors of 36: 2*2*3*3 = 2²*3²
Step 2: Find the LCM of 32 and 36.
The LCM is found by multiplying the highest power of all the factors that appear in either number. Here we have 2⁵ from 32 and 2²*3² from 36. The higher power of 2 is 2⁵ from 32 and the higher power of 3 is 3² from 36. So, LCM = 2⁵*3² = 32*9 = 288
Step 3: Find the HCF of 32 and 36.
The product of two integers (32 and 36) is equal to the product of their HCF and LCM. So, we can find the HCF by dividing the product of the two numbers by their LCM.
HCF = (32*36) / LCM
= (32*36) / 288
= 4
Therefore, the HCF of 32 and 36 is 4. Hence, the correct option is (b) 4.
Q3: 36 can be expressed as a product of its primes as
(a) 2² х 3²
(b) 2¹ х 3³
(c) 2³ х 3¹
(d) 2⁰ х 3⁰
Ans: (a)
Explanation: Prime factorization is the process of breaking down a number into its smallest prime factors. A prime number is a number that has only two distinct positive divisors: 1 and itself. For example, the first six prime numbers are 2, 3, 5, 7, 11, and 13.
To express 36 as a product of its primes, we follow these steps:
Step 1: Begin by dividing the number 36 with the smallest prime number, i.e., 2. 36 divided by 2 is 18.
Step 2: Now divide 18 by 2 to get 9.
Step 3: As 9 cannot be divided by 2, we move to the next prime number, which is 3. 9 divided by 3 is 3.
Step 4: Finally, divide 3 by 3 to get 1. Now we stop because we have reached 1.
The prime factors of 36 are therefore 2, 2, 3, and 3. We write this as 2² х 3².
So, the answer is (a) 2² х 3².
Q4: 7 х 11 х 13 х 15 + 15 is a
(a) Prime number
(b) Composite number
(d) Neither prime nor composite
(d) None of the above
Ans: (b)
Explanation: The question is asking to determine the type of number 15 is, when it's part of the given multiplication equation.
Step 1: Let's understand the definitions first.
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, and 13.
A composite number is a positive integer that has at least one positive divisor other than one or itself. In other words, a composite number is any positive integer greater than one that is not a prime number.
Step 2: Now, consider the number 15.
We can see that 15 is not a prime number because it has more than two factors, which are 1, 3, 5, and 15.
Step 3: Therefore, 15 is a composite number.
Hence, the correct option is (B).
Q5: If p and q are positive integers such that p = ab² and q = a²b, where a, b are prime numbers, then the LCM (p, q) is
(a) ab
(b) a²b²
(c) a³b²
(d) a³b³
Ans: (b)
Explanation: Let's break down the solution to understand it better.
Firstly, we are given two positive integers, p and q which are represented as p = ab² and q = a²b, where a and b are prime numbers.
The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. In other words, it is the smallest number that both numbers can divide into evenly.
When finding the LCM of two numbers represented as the product of prime numbers raised to some powers (as in this case), the LCM is simply the product of these primes each raised to the highest power that appears in either number.
In this case, the prime number 'a' is raised to the first power in p and to the second power in q. Thus, in the LCM, 'a' is raised to the highest power of these, which is 2.
Similarly, the prime number 'b' is raised to the second power in p and to the first power in q. In the LCM, 'b' is raised to the highest power of these, which is 2.
Hence, the LCM of p and q is a²b² which corresponds to option (b).
So, the correct answer is option (b) a²b².
|
29 videos|254 docs|56 tests
|
















