Class 10 Maths Chapter 1 HOTS Questions - Real Numbers
HOTS
Q1. Show that 6n cannot end with the digit 0.
Ans:
∵ All composite numbers ending with 0 have 10 as a factor.
∴10 is a factor of 6n
∴ We have: 6n = 10 × p, where p is a natural number
⇒ (2 × 3)n = 2 × 5 × p
⇒ 2n × 3n = 2 × 5 × p
i.e. 5 is a prime factor of 2n × 3n which is not possible.
Thus, our assumption was wrong and 6n cannot end with the digit 0.
Q2. Show that there is no integer for which is rational.
is rational.
Ans:
If possible, let ‘n’ be a positive integer such that is rational.
is rational.
Let 

(using componendo and dividendo)
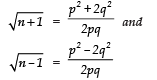
Since  are rational numbers.
are rational numbers.
∴  are also rational.
are also rational.
i.e.  are perfect squares of +ve integers. It is not possible.
are perfect squares of +ve integers. It is not possible.
[∵ two perfect squares differ by 3] ⇒ Our assumption is not possible.
Q3. If  is an irrational number, then show that
is an irrational number, then show that is also irrational.
is also irrational.
Ans:
If possible, let be a rational number.
be a rational number.

But it contradicts our assumption that is irrational. Thus,
is irrational. Thus, is irrational.
is irrational.
Q4. How many prime numbers are there of the form 10n + 3, where n is a whole number 1 < n < 10?
Ans:
Substituting 1, 2, 3, .................... 10 in 10 n + 3, we have: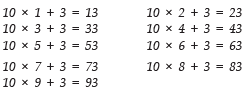
Thus, the required numbers are 13, 23, 43, 53, 73 and 83.
Value-Based Questions
Q5. To raise funds for an orphanage various sports activities are planned in a school. In a cycling activity around a circular field Sonia takes 24 minutes to complete one round of the field while Ram takes 18 minutes for the same, suppose they both start at the same point and at the same time and go in the same direction
(i) After how many minutes will they meet again at the starting point?
(ii) Which concept of mathematics is used in the above problem?
(iii) By organising sports activities for raising funds for an orphanage which value is depicted by the school?
Ans:
(i) Time taken by Sonia to complete a round = 24 minutes
Time taken by Ram to complete a round = 18 minutes
The LCM of 24 and 18 gives the exact-number of minutes after which they meet at the starting point again.
24 = 2 × 2 × 2 × 3
18 = 2 × 3 × 3
∴ LCM of 24 and 18 = 2 × 2 × 2 × 3 × 3 = 72
⇒ They will meet again at the starting point-after 72 minutes.
(ii) Real numbers
(iii) Helping needy persons.
Q6. A dairy owner decided to supply pure milk to his customers. He collected 120 litres of pure cow-milk and 180 litres of pure buffalo-milk. He fills the two kinds of milk in containers of equal capacity.
(i) What is the greatest capacity of such container?
(ii) Which mathematical concept is used in the above problem?
(iii) By supplying pure-milk which value is depicted by the dairy-owner?
Ans:
(i) The maximum capacity of a pack of milk is equal to the HCF of 120 and 180.
We have
∴ HCF of 120 and 180 = 60
⇒ Capacity of each container = 60 litre
(ii) Real Numbers
(iii) Positive contribution to social-health.
Q7. In a food safety drive a team of food inspectors collected samples of adulterated 420 pieces of burfis and 148 pieces of ladoos. They want to pack these pieces in such a way that each pack has the same number of pieces of sweets.
(i) What is the maximum number of sweets pieces that can be placed in each pack?
(ii) Which mathematical concept is used in the above problem?
(iii) By collected the samples of adulterated sweets which value is depicted by the food inspectors?
Ans:
(i) For packing maximum number of sweets pieces in each pack, we find the HCF of 420 and 148.
∴ We have

⇒ HCF of 420 and 148 is 4.
⇒ Required number of sweets pieces
= 4
(ii) Real numbers
(iii) Check on public health.
Q8. A school has a book bank for the help of students from the economically weaker section. Students of class X donated the following number of books to the book bank.
English : 96
Hindi : 240
Mathematics : 336
These books have to be stacked in such a way that all the books are stored topic-wise and number of copies in each stack is the same.
(i) What is the maximum number of books in each stack?
(ii) Which mathematical concept is used in the above problem?
(iii) By donating books through the school book bank which value is depicted by the students of class X?
Ans:
(i) Maximum number of books in each pack is the HCF of 96, 240 and 336.
⇒ HCF of 96, 240 and 336 is 48.
⇒ The required maximum number of copies in each pack
= 48
(ii) Real numbers
(iii) Charity
Q9. Raghunath has to distribute bananas to the inhabitants of old-age-homes in a town. There are two old-age homes in the town—home-A and home-B. There are 32 old persons in home-A and 36 old persons in home B.
(i) Determine the minimum number of bananas required for the two old-age-homes that can be distributed equally among the inhabitants of home-A or home-B.
(ii) Which mathematical concept is used in the above problem?
(iii) By donating bananas to inhabitants of old-age homes which value is depicted by Raghunath?
Ans:
(i) The bananas are to be distributed equally among old persons of home-A and home-B.
The required number of bananas is the least multiple of 32 as well as 36.
Since, 32 = 2 × 2 × 2 × 2 × 2
= 25
36 = 2 × 2 × 3 × 3
= 22 × 32
∴ LCM of 32 and 36 = 25 × 32
= 288
Required number of bananas
= 288
(ii) Real numbers
(iii) Positive attitude towards senior citizens.
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 1 HOTS Questions - Real Numbers
| 1. What are real numbers? |  |
| 2. How are real numbers classified? |  |
| 3. What is the significance of real numbers in mathematics? |  |
| 4. What is the difference between rational and irrational numbers? |  |
| 5. How are real numbers used in real-life situations? |  |

|
Explore Courses for Class 10 exam
|

|


















