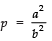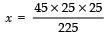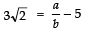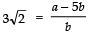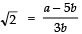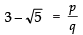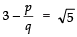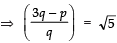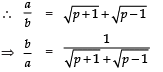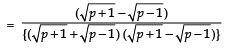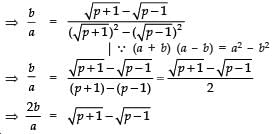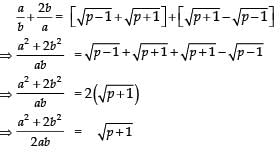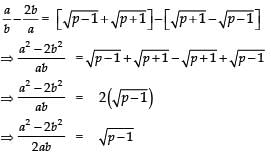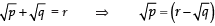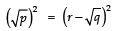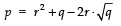Class 10 Maths Chapter 1 Question Answers - Real Numbers - 1

Q1: The decimal representation of 6/1250 will terminate after how many places of decimal?

1. Simplify the fraction to its lowest form.

2. Now we can either convert the lowest fraction into decimals or a quicker way to do this is to convert the denominator to a multiple of 10 so that it is easier to convert it into decimals.
3. So we multiply with and divide by  2⁴ to convert the denominator to 10^4. 
24 2

 

Therefore, this representation will terminate after 4 decimal places.

Q2: If ‘p’ is prime, prove that √p is irrational.

Let √p be rational in the simplest form a/b, where p is prime.
∴ a and b are integers having no common factor other than 1 and b ≠ 0.
⇒ Now, √p = a/b
⇒ Squaring both sides, we have
 
⇒ pb² = a²      ...(1)
⇒ Since pb² is divisible by p, a² is also divisible by p.
⇒ a is also divisible by p    ...(2)
Let a = pc for some integer c.
⇒ Substituting a = pc in (1), we have
pb² = (pc)²
⇒ pb² = p²c²
⇒ b²  = pc²
pc² is divisible by p,
∴ b² is divisible by p
⇒ b is divisible by p    ...(3)
From (2) and (3),
⇒ p is a common factor of ‘a’ and ‘b’. But this contradicts our assumption that a and b are co-prime.
∴ Our assumption that √p is rational is wrong. Thus, √p is irrational if p is prime.

Q3: Find the HCF of 18 and 24 using prime factorisation.

Using factor tree method, we have:


∴ 18 = 2 × 3 × 3 = 2 × 3²
24 = 2 × 2 × 2 × 3 = 2³ × 3
HCF = Product of common prime factors with lowest powers.
⇒ HCF (18, 24) = 3 × 2  = 6

Q4: Find the LCM of 10, 30 and 120.

                                    
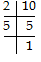
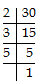
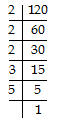
∴ 10 = 2 × 5 = 2¹ × 5¹
30 = 2 × 3 × 5 = 2¹ × 3¹ × 5¹
120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3¹ × 5¹
LCM = Product of each prime factor with highest powers
⇒ LCM of 10, 30 and 120 = 2³ × 3 × 5 = 120.

Q5: Express as a rational number in the simplest form.

Let x =  = 0.666 .....    ...(1)
∴ 10x = 0.666 ..... × 10
10 x = 6.666 .......(2)
Subtracting (1) from (2), we have:
⇒ 10x - x = 6.666 ..... - 0.666 .....
⇒ 9x = 6
⇒ x = 6/9 = 2/3  
Thus,= 2/3

Q6: Express  as a rational number in the simplest form.

Let    x  =    = 1.161616 ........(1)
∴ 100x = (1.161616 .....) × 100
⇒ 100x = 116.161616 ........(2)
Subtracting (1) from (2), we have:
100x - x = [116.161616 .....] – [1.161616 .....]
⇒ 99x = 115
⇒ x = 115/99  
Thus,   =115/99

Q7: Use Euclid's division algorithm to find HCF of 870 and 225.

We have 870 = 3 × 225 + 195
⇒ 225 = 1 × 195 + 30
⇒ 195 = 6 × 30 + 15
⇒ 30 = 2 × 15 + 0
∴ HCF (870, 225) is 15.

Q8: Find the LCM and HCF of 1296 and 5040 by prime factorisation method.

  and      
∴ 5040 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 7
= 2⁴ × 3² × 5 × 7  and
⇒ 1296 =  2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
= 2⁴ × 3⁴
∴ LCM = Product of each prime factor with highest powers
=  2⁴ × 3⁴ × 5 × 7
= 16 × 81 × 5 × 7 = 45360
HCF = Product of common prime factors with lowest powers
= 2⁴ × 3²
= 16 × 9 = 144

Q9: Prove that √3 is irrational.

Let √3 be rational in the simplest form of P/q.
i.e., p and q are integers having no common factor other than 1 and q ≠ 0.
Now,   √3 = p/q  
Squaring both sides, we have
⇒ (√3)² = (p/q)²
⇒ 3 = p²/q²   
⇒ 3q² = p² ............(1)
Since 3q² is divisible by 3
∴ p² is also divisible by 3
⇒ p is divisible by 3 ..........(2)
Let p = 3c for some integer ‘c’.
Substituting p = 3c in (1), we have:
⇒ 3q²  = (3c)²
⇒ 3q² = 9c²
⇒ q²  = 3c²
3c² is divisible by 3
∴ q² is divisible by 3
⇒ q is divisible by 3   ...(3)
From (2) and (3)
3 is a common factor of ‘p’ and ‘q’. But this contradicts our assumption that p and q are having no common factor other than 1.
∴ Our assumption that √3 is rational is wrong.
Thus, √3 is an irrational.

Q10: Show that  3√2 is irrational.

Let 3√2 be a rational number
∴ p/q = 3√2 where p and q are prime to each other and q ≠ 0.
∴ p/3q = √2   ...(1)
Since, p is integer and 3q is also integer (3q≠ 0).
∴ p/3q is a rational number.
From (1), √2 is a rational number.
But this contradicts the fact that √2 is irrational. Therefore, our assumption that 3√2 is rational is incorrect.
Hence, 3√2 is irrational.

Q11: Show that 2 - √3 is an irrational number.

Let  2 - √3 is rational.
∴ It can be expressed as p/q where p and q are integers (prime to each other) such that q ≠ 0.
∴  2 - √3   =  p/q  
⇒      ...(1)

∵ p is an integer}
∴ q is an integer}
⇒ p/q is a rational number.
∴  is a rational number.   ...(2)
From (1) and (2), √3 is a rational number. This contradicts the fact that √3 is an irrational number.
∴ Our assumption that (2 -√3) is a rational number is not correct. Thus, (2 - √3) is irrational.

Q12: Using Euclid’s division algorithm, find the HCF of 56, 88 and 404. 

Q13: Express  in the decimal form.

We have

[multiplying and dividing by 5]

 

Q14: Express   in the p/q form.

Let    x    =    
or x = 5.4178178178 .....
∴ 10x = 54.178178178 ........(1)
Also 1000 (10x) = 54178.178178178 .....
⇒ 10000x    =    54178.178178178 ........(2)
Subtracting (1) from (2), we have:
⇒ 10000x - 10x    
= [54178.178178.....] - [54.178178 .....]
⇒ 9990x = 54124

⇒
Thus,

Q15: State whether   is a rational number or not.

 = 1.23333..... is a non-terminating repeating decimal.
∴ is a rational number.
3/4 is in the form of p/q, where q ≠ 0  [Here 4 ≠ 0]
∴ 3/4 is a rational number.
Since the sum of two rational numbers is a rational number.
Therefore,   is a rational number.

Q16: The LCM of two numbers is 45 times their HCF. If one of the numbers is 225 and sum of their LCM and HCF is 1150, find the other number.

One of the numbers = 225
Let the other number = x
Also LCM = 45 (HCF)                 ...(1)
And LCM + HCF =1150
⇒ (45 HCF) + HCF = 1150
⇒ 46 HCF = 1150
⇒ HCF = 1150/46 = 25
From (1),
LCM = 45 × 25
∴ LCM × HCF = (45 × 25) × 25
Now,  LCM × HCF = Product of the numbers
∴  x × 225 = (45 × 25) × 25
⇒

= 125
Thus, the required number is 125.

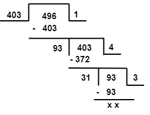
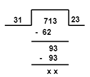
Q17: Three different containers contain 496 litres, 403 litres and 713 litres of a mixture. What is the capacity of the biggest container that can measure all the different quantities exactly?

For the capacity of the biggest container, we have to find the HCF.

HCF: By Long Division method

First find the HCF of two numbers, 496 and 403

The HCF of 496 and 403 = 31
Now find the HCF of 31 and 713

HCF of 713 and 31 is 31
So, the maximum capacity is 31 liters.

Q18: Prove that 3+√2 is an irrational number.  

Let 3 + √2 is a rational number.
∴ 3 + √2  = a/b such that ‘a’ and ‘b’ are co-prime integers and b ≠ 0.
We have

 Since a and b are integers,
∴   is rational.
⇒    √2 is a rational. This contradicts the fact that √2 is irrational.
∴ Our assumption that 3 + √2 is rational is not correct.
⇒ (3 + √2) is an irrational number.

Q19: Prove that 5-2√3 is an irrational number.
Sol:

Let 5-2√3 is a rational number
∴ 5-2√3= p/q  where p and q are co-prime integers and q ≠ 0.

Since, p and q are integers.
∴  p/2q is a rational number
i.e.,   is a rational number.
⇒√3 is a rational number.
But this contradicts the fact that √3 is an irrational number.
So, our assumption that (5-2√3) is a rational number is not correct.
∴ (5-2√3) is an irrational number.

Q20: Prove that (5+3√2) is an irrational number.

Sol: 

Let (5+3√2) is a rational number.
∴ (5+3√2) =  a/b [where ‘a’ and ‘b’ are co-prime integers and b ≠ 0

⇒
⇒
⇒

‘a’ and ‘b’ are integers,
∴   is a rational number.
⇒ √2 is a rational number.
But this contradicts the fact that √2 is an irrational number.
∴ Our assumption that (5+3√2) is a rational is incorrect.
⇒ (5+3√2) is an irrational number.

Q21: Use Euclid’s Division Lemma to show that the square of any positive integer is either of the form ‘3m’ or ‘3m + 1’ for some integer ‘m’.

Sol: 

Let x be a positive integer
∴ x can be of the form 3p, (3p + 1) or (3p + 2)
When x = 3p,  we have
x² = (3p)²
⇒ x² = 9p²
⇒ x²  = 3 (3p²)
⇒ x² = 3m [Here 3p² = m]
When x  = (3p + 1),  we have
x² =  (3p + 1)²
⇒ x² = 9p² + 6p + 1
⇒ x² = 3p (3p + 2) + 1    
= 3m + 1,
Where m =p (3p +2)
When x   = 3p +2 ,  we have
x² = (3p + 2)²
= 9p² + 12p + 4
= 9p² + 12p + 3 + 1
= 3 (3p² + 4p + 1) + 1
= 3m + 1,  where
m  = 3p² + 4p + 1
Thus, x² is of the form 3m or 3m + 1.

Q22: Show that one and only one of n, n + 2 and n + 4 is divisible by 3. 

Sol: 

Let n be any integer. When dividing n by 3, there are three possible remainders, 0, 1, or 2. So, n can be written in one of the following forms:

1. $n\; =\; 3q$n=3q (remainder 0)
2. n=3q+1 (remainder 1)
3. n=3q+2 (remainder 2)

Now, we will check the divisibility of $n$n, n+2, and n+4 in each case:

Case 1: n = 3q

• n = 3q, so $n$n is divisible by 3.
• $n\; +\; 2\; =\; 3q\; +\; 2$n+2 = 3q+2, which leaves a remainder of 2 when divided by 3, so n+2 is not divisible by 3.
• n+4 = 3q+4 = 3(q+1)+1, which leaves a remainder of 1 when divided by 3, so n+4 is not divisible by 3.

Thus, in this case, $nn$n is divisible by 3, but $n+2n\; +\; 2$n+2 and $n+4n\; +\; 4$n+4 are not.

Case 2: n = 3q+1

• n=3q+1, which leaves a remainder of 1 when divided by 3, so $n$n is not divisible by 3.
• $n\; +\; 2\; =\; 3q\; +\; 1\; +\; 2\; =\; 3q\; +\; 3\; =\; 3(q\; +\; 1)$n+2 = 3q+1+2 = 3q+3 = 3(q+1), so $n\; +\; 2$n+2 is divisible by 3.
• n+4 = 3q+1+4 = 3q+5 = 3(q+1)+2, which leaves a remainder of 2 when divided by 3, so $n\; +\; 4$n+4 is not divisible by 3.

Thus, in this case, n+2 is divisible by 3, but n and $n\; +\; 4$n+4 are not.

Case 3: n = 3q + 2

• $n\; =\; 3q\; +\; 2$n=3q+2, which leaves a remainder of 2 when divided by 3, so n is not divisible by 3.
• $n\; +\; 2\; =\; 3q\; +\; 2\; +\; 2\; =\; 3q\; +\; 4\; =\; 3(q\; +\; 1)\; +\; 1$n+2 = 3q+2+2 = 3q+4 = 3(q+1)+1, which leaves a remainder of 1 when divided by 3, so $n\; +\; 2$n+2 is not divisible by 3.
• $n\; +\; 4\; =\; 3q\; +\; 2\; +\; 4\; =\; 3q\; +\; 6\; =\; 3(q\; +\; 2)$n+4 = 3q+2+4 = 3q+6 = 3(q+2), so $n\; +\; 4$n+4 is divisible by 3.

Thus, in this case, $n\; +\; 4$n+4 is divisible by 3, but $n$n and n+2 are not.

Conclusion:

In each of the three cases, exactly one of $n$n, $n\; +\; 2$n+2, or $n\; +\; 4$n+4 is divisible by 3, and the other two are not. Therefore, one and only one of $n$n, n+2, or $n\; +\; 4$n+4 is divisible by 3.

Q23: Show that (2+√5 )is an irrational number.

Sol: 

Let (2+√5)  is a rational number.
∴ (2+√5) = p/q  , such that p and q are co-prime integers and q ≠ 0

p and q are integers.
∴   is a rational.
⇒ √5 is a rational.
But, this contradicts the fact that √5 is an irrational.
∴ Our supposition that (2+√5) is rational is incorrect.
Thus,(2+√5)is an irrational.

Q24: Prove that 3-√5 is an irrational number.

Sol: 

Let (3-√5) is a rational number.
∴ 3-√5 = p/q , such that p and q are co-prime integers and q ≠ 0.

⇒
⇒

Since, p and q are integers,
∴  is a rational number.
⇒ √5 is a rational number.
But this contradicts the fact that √5 is an irrational number.
∴ Our assumption that (3-√5)  is a rational number’ is incorrect.
⇒ (3-√5)  is an irrational number.

Q25: Prove that (5+ √2) is irrational.

Sol: 

√2 = a/b where ‘a’ and ‘b’ are co-prime integers and b ≠ 0

⇒
⇒

since ‘a’ and ‘b’ are integers,
∴  is a rational.
⇒ √2 is a rational.
But this contradicts the fact that √2 is an irrational.
∴ Our assumption that (5+ √2) is a rational number is incorrect.
Thus, (5+ √2) is an irrational number.

Q26: Prove that 2√3-7 is an irrational.

Sol: 

Let  2√3-7 is rational.

⇒
∵p and q are integers.
∴   is rational.
⇒ √3 is rational.
But we know that √3 is irrational,
∴ Our assumption that (2√3-7) is rational is wrong.
Hence 2√3-7 is irrational.

Q27: If ‘n’ in an odd  integer, then show that n² – 1 is divisible by 8.

Sol: 

Le q be an integer, then
4q + 1 or 4q + 3
Now,

 When n is odd

• Any odd integer can be written as $n=2k+1n\; =\; 2k\; +\; 1$n=2k+1, where $kk$k is an integer.
• Then: $n\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}=(2k+1)\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}=4k\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}+4k+1n^2\; =\; (2k\; +\; 1)^2\; =\; 4k^2\; +\; 4k\; +\; 1$      $\mathrm{ \; \; n}\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}-1=(4k\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}+4k+1)-1=4k(k+1)n^2\; -\; 1\; =\; (4k^2\; +\; 4k\; +\; 1)\; -\; 1\; =\; 4k(k\; +\; 1)$
• Since $k(k\; +\; 1)$k(k+1) is always an even number (the product of two consecutive integers), we can write: $n\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}-1=8\mathrm{m }for\; some\; integer$for some integer m.

Q28: Prove that if x and y are both odd positive integers, then x² + y² is even but not divisible by 4.

Sol:

Let $x\; =\; 2m\; +\; 1$x=2m+1 and $y\; =\; 2n\; +\; 1$y=2n+1, where m and $n$n are integers (since x and y are odd integers).

Now:

x² = (2m+1)² = 4m²+4m+1       $y^2\; =\; (2n\; +\; 1)^2\; =\; 4n^2\; +\; 4n\; +\; 1$y² =(2n+1)² = 4n² + 4n+1

Adding these:

x² + y² = (4m²+4m+1) + (4n²+4n+1) = 4(m²+n²+m+n) + 2

Thus, x² + y² = 4q+2, where $q\; =\; m^2\; +\; n^2\; +\; m\; +\; n$q=m²+n²+m+n.

Since $x\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}+y\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}$ is of the form $4q+24q\; +\; 2$, it is an even number but not divisible by 4 (because it leaves a remainder of 2 when divided by 4).

Therefore, $x\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}+y\mathrm{<sup\; style="letter-spacing:\; inherit\; !important;">2</sup>}x^2\; +\; y^2$ is even but not divisible by 4.

Q29: Show that the square of an odd positive integer can be of the form 6q + 1 or 6q + 3 for some integer q.

Sol: 

Let ‘m’ be an integer such that 6m, 6m + 1, 6m + 2, 6m + 3, 6m + 4 or 6m + 5 can be any positive integer.
∴ An odd positive integer can be of the form 6m + 1, 6m + 3  or 6m + 5
Now, we have
(6m + 1)²  =  36m² + 12m + 1
= 6(6m² + 2m) + 1
= 6q + 1, q is an integer
(6m + 3)²  =  36m² + 36m + 9    
= 6(6m² + 6m + 1) + 3
= 6q + 3, q is an integer
(6m + 5)² = 36m² + 60m + 25    
= 6(6m² + 10m + 4) + 1
= 6q + 1,  q is an integer
Thus, the square of an odd positive integer can be of the form 6q + 1 or 6q + 3.

Q30: Show that one and only one out of n, n + 4, n + 8, n + 12 and n + 16 is divisible by 5, where n is any positive integer.

Sol: 

Let $n=5k+rn\; =\; 5k\; +\; r$, where $kk$ is an integer and $r$ is the remainder when $nn$ is divided by 5. The possible values of $r$r are 0, 1, 2, 3, or 4.

We will check each value of $r$r and see which one leads to a multiple of 5.

Case 1: r = 0

• $n=5k$, so $n$n is divisible by 5.
• $n+4=5k+4n\; +\; 4\; =\; 5k\; +\; 4$, not divisible by 5.
• $n+8=5k+8=5(k+1)+3n\; +\; 8\; =\; 5k\; +\; 8\; =\; 5(k\; +\; 1)\; +\; 3$, not divisible by 5.
• $n+12=5k+12=5(k+2)+2n\; +\; 12\; =\; 5k\; +\; 12\; =\; 5(k\; +\; 2)\; +\; 2$, not divisible by 5.
• $n+16=5k+16=5(k+3)+1n\; +\; 16\; =\; 5k\; +\; 16\; =\; 5(k\; +\; 3)\; +\; 1$, not divisible by 5.

Thus, only $n$n is divisible by 5.

Case 2: r = 1

• $n=5k+1n\; =\; 5k\; +\; 1$, not divisible by 5.
• $n+4=5k+5n\; +\; 4\; =\; 5k\; +\; 5$, divisible by 5.
• $n+8=5k+9=5(k+1)+4n\; +\; 8\; =\; 5k\; +\; 9\; =\; 5(k\; +\; 1)\; +\; 4$, not divisible by 5.
• $n+12=5k+13=5(k+2)+3n\; +\; 12\; =\; 5k\; +\; 13\; =\; 5(k\; +\; 2)\; +\; 3$, not divisible by 5.
• $n+16=5k+17=5(k+3)+2n\; +\; 16\; =\; 5k\; +\; 17\; =\; 5(k\; +\; 3)\; +\; 2$, not divisible by 5.

Thus, only n+4 is divisible by 5.

Case 3: r = 2

• $n=5k+2n\; =\; 5k\; +\; 2$, not divisible by 5.
• $n+4=5k+6n\; +\; 4\; =\; 5k\; +\; 6$, not divisible by 5.
• $n+8=5k+10n\; +\; 8\; =\; 5k\; +\; 10$, divisible by 5.
• $n+12=5k+14=5(k+2)+4n\; +\; 12\; =\; 5k\; +\; 14\; =\; 5(k\; +\; 2)\; +\; 4$, not divisible by 5.
• $n+16=5k+18=5(k+3)+3$, not divisible by 5.

Thus, only $n+8n\; +\; 8$n+8 is divisible by 5.

Case 4: r = 3

• $n=5k+3n\; =\; 5k\; +\; 3$, not divisible by 5.
• $n+4=5k+7=5(k+1)+2n\; +\; 4\; =\; 5k\; +\; 7\; =\; 5(k\; +\; 1)\; +\; 2$, not divisible by 5.
• $n+8=5k+11=5(k+2)+1n\; +\; 8\; =\; 5k\; +\; 11\; =\; 5(k\; +\; 2)\; +\; 1$, not divisible by 5.
• $n+12=5k+15n\; +\; 12\; =\; 5k\; +\; 15$, divisible by 5.
• $n+16=5k+19=5(k+3)+4n\; +\; 16\; =\; 5k\; +\; 19\; =\; 5(k\; +\; 3)\; +\; 4$, not divisible by 5.

Thus, only n+12 is divisible by 5.

Case 5: r = 4

• $n=5k+4n\; =\; 5k\; +\; 4$, not divisible by 5.
• $n+4=5k+8=5(k+1)+3n\; +\; 4\; =\; 5k\; +\; 8\; =\; 5(k\; +\; 1)\; +\; 3$, not divisible by 5.
• $n+8=5k+12=5(k+2)+2n\; +\; 8\; =\; 5k\; +\; 12\; =\; 5(k\; +\; 2)\; +\; 2$, not divisible by 5.
• $n+12=5k+16=5(k+3)+1n\; +\; 12\; =\; 5k\; +\; 16\; =\; 5(k\; +\; 3)\; +\; 1$, not divisible by 5.
• $n+16=5k+20n\; +\; 16\; =\; 5k\; +\; 20$, divisible by 5.

Thus, only $n+16n\; +\; 16$ is divisible by 5.

Q31: Show that there is no positive integer ‘p’ for which 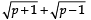is rational.

Sol: 

If possible let there be a positive integer p for which  = a/b is equal to a rational i.e. where a and b are positive integers.

Now

Also,

Since a, b are integer

 are rationals

⇒ (p + 1) and (p – 1) are perfect squares of positive integers, which is not possible (because any two perfect squares differ at least by 3). Hence, there is no positive integer p for which  is rational.

Q32: Prove that 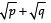is irrational, where p and q are primes.

Sol: 

Let be rational
Let it be equal to ‘r’
i.e.
Squaring both sides, we have

⇒
⇒   ...(i)
Since, p, q are both rationals
Also, r² is rational (∵ r is rational)
∴ RHS of (i) is a rational number
⇒ LHS of (i) should be rational i.e.√q  should be rational.
But √q is irrational (∵ p is prime).
∴ We have arrived at a contradiction.
Thus, our supposition is wrong.
Hence, √p+√q  is irrational.