Class 10 Maths Chapter 10 Practice Question Answers - Circles
Q1. If the angle between two radii of a circle is 100º , the angle between the tangents at the ends of those radii is:
(a) 50º
(b) 60º
(c) 80º
(d) 90º
Ans: (c)
Sol:
From the figure, it is evident that ∠AOB=100º .
Now, ∠OAP=90º and ∠OBP=90º (radii is perpendicular to tangent at point of contact)
Also, sum of interior angles of a quadrilateral is 360º and hence,
∠APB=360º −∠OAP−∠OBP−∠AOB=80º
This is the required angle between the tangents.
Q2. Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm
Ans: (b)
Sol:
Two concentric circles have the centre as O.
AB is a chord of the outer circle and AB touches the inner circle at T.
OA=OB=5cmandAB=8cm.
To find out −
The radius of the inner circle i.e OT=?
Solution−
AB touches the inner circle at T.
So the line OT from the centre O to Tis perpendicular to AB at T.
i.e ∠OTA = 90º =∠OTB.....(i)
∴ Between ΔOTA & ΔOTB we have
OA = OB = 5 cm (given)
∠OTA =∠OTB=90º (from i)
∴ ΔOTA & ΔOTB are congruent by SAS test.
⟹AT=BT or AT= 1/2 ×AB
⟹AT= 1/2 × 8cm=4cm.
Now in ΔOTA we have ∠OTA=90º
i.e ΔOTA is right angled at T with OA as hypotenuse.
∴ Applying Pythagoras theorem, we have,
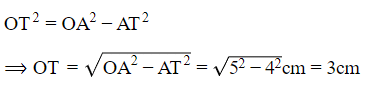
So the radius of the inner circle 3cm.
Q3. Radius of a circle with centre 'O' is 5 cm. P is a point at a distance of 3 cm from 'O'. Then the number of tangents that can be drawn to the circle is
(a) 1
(b) 2
(c) 0
(d) 3
Ans: (c)
Sol:
To determine the number of tangents that can be drawn to the circle, we need to consider the relative position of the point P with respect to the circle.
If a point is located inside the circle, there are no tangents that can be drawn to the circle.
If a point is located on the circle, there is exactly one tangent that can be drawn to the circle at that point.
If a point is located outside the circle, there are exactly two tangents that can be drawn to the circle from that point.
In this case, the point P is located at a distance of 3 cm from the center of the circle, which is less than the radius of the circle (5 cm). Therefore, the point P is located inside the circle. Hence, no tangents can be drawn to the circle from the point P.
Therefore, the answer is (c) 0.
Q4. There is no tangent to a circle passing through a point lying ..... the circle.
(a) inside
(b) outside
(c) on the circle
(d) none of these
Ans: (a)
Sol: Tangent touches the circle at one point only and so it is not possible for a point inside a circle.
Q5. In the given figure, if OC = 9 cm and OB = 15 cm, then BC + BD is equal to: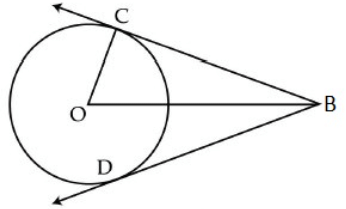 (a) 18cm
(a) 18cm
(b) 12cm
(c) 24cm
(d) 36 cm
Ans: (c)
Sol:
We know that, a tangent to a circle is perpendicular to the radius at the point of contact.
So, △OCB is right a triangle, right angled at C.
Hence, by Pythagoras' theorem, we have:
We also know that, the tangents drawn from the same external point to a circle are equal.
Since BC and BD are tangents drawn from the same external point, B, we have:
BC=BD=12 cm.
So, BC+BD=24 cm.
Hence, BC+BD=24 cm.
Q6. In the given figure, tangents PQ and PR are drawn from an external point p to a circle with center O, such that ∠RPQ=30º . A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
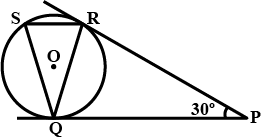
Sol:
∠RPQ is given as 30º, and we want to find ∠RQS.
Step 1: Find ∠RPQ + ∠RQS
Since PQ is a tangent to the circle at point Q, and RS is a chord parallel to PQ, we have:
∠RPQ = ∠RQS (Alternate segment theorem)
Step 2: Substitute the known angle value
∠RPQ + ∠RQS = 30º + ∠RQS
Step 3: Use the fact that angles in a triangle add up to 180º
Since QSR is a triangle, we have:
∠RQS + ∠QRS + ∠QSR = 180º
Step 4: Substitute the known angle value
∠RQS + 30º + ∠QSR = 180º
Step 5: Solve for ∠RQS
∠RQS = 180º - 30º - ∠QSR
∠RQS = 150º - ∠QSR
Now, we need to find ∠QSR. Since RS is a parallel chord, we can use the fact that alternate interior angles are equal when a transversal intersects parallel lines. Thus, ∠QSR = ∠RPQ = 30º.
Now we can find ∠RQS:
∠RQS = 150º - 30º
∠RQS = 120º
So, the measure of ∠RQS is 120 degrees.
Q7. The maximum number of common tangents that can be drawn to two circles intersecting at two distinct points is
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol:
only two common tangents are possible
because circles intersect at two points.
Q8. If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is
(a) 3cm
(b) 6cm
(c) 9 cm
(d) 1 cm
Ans: (b)
Sol:
Given−
The radii of two concentric cirles with centre O are 5cm&4cm.
The chord AB of outer circle touches the inner circle at P.
To find out−
The length of AB=?.
The radius of a circle is at the right angle at the point of contact of the tangent to the circle with the tangent.
Solution−
AB touches the inner circle at P.
∴ AB=2AP, OP⊥AB
⟹ΔAOP is a right angled one with AO as the hypotenuse.
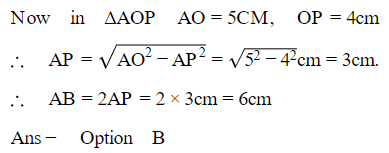
Q9. In the given figure, O is the centre of a circle of radius 5 cm, T is a point such that OT= 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.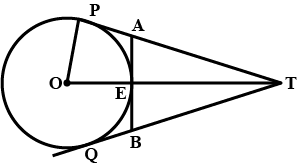
Sol:
OP=OQ=5cm
OT=13cm
OP and PT are radius and tangent respectively at contact point P.
∴ ∠OPT=90 º
So, by pythagoras theorem, in right angled ΔOPT,
PT2 = OT2 −OP2 =132 - 52 =169−25=144
⇒PT=12cm
AP and AE are two tangents from an external point A to a circle.
∴ AP=AE
AEB is tangent and OE is radius at contact point E.
So, AB⊥OT ___(i)
So, by Pythagoras theorem, in right angled. ΔAET.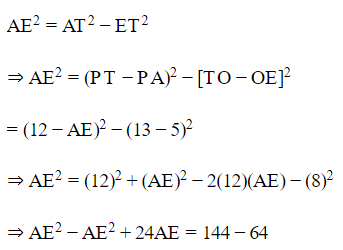
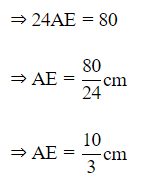
In ΔTPO and ΔTQO,
OT=OT [common]
PT=QT [Tangents from T]
OP=OQ [Radii of same circle]
∴ ΔTPO≅ΔTQO [By SSS criterion of congruence]
⇒∠1=∠2 ___(ii) [CPCT]
In ΔETA and ΔETB,
ET=ET [Common]
∠TEA=∠TEB=90º
[From (i)]
∠1=∠2 [CPCT] [From (ii)]
∴ ΔETA ≅ ΔETB [By ASA criterion of congruence]
⇒AE=BE [CPCT]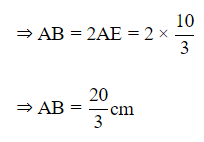
Hence, the required length is 20/3 cm.
Q10. There is only one tangent at any point on the circumference of a circle. Say true or false
(a) True
(b) False
(c) Ambiguous
(d) Data insufficient
Ans: (a)
Sol: Only one tangent possible at a point on the circumference of a circle.
|
127 videos|584 docs|79 tests
|





















