Class 10 Maths Chapter 11 Previous Year Questions - Areas Related to Circles
Previous Year Questions 2024
Q1: The Perimeter of a sector of a circle whose central angle is 90º and radius 7 cm is: (CBSE 2024)(a) 35 cm
(b) 11 cm
(c) 22 cm
(d) 19.5 cm
 View Answer
View Answer 
Ans: (d)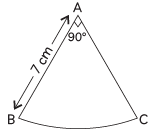
Perimeter of sector
= 2r +πr θ360°
= 2 × 7 + 227 × 7 × 90°360°
= 14 + 5.5 = 19.5 cm
Q2: A stable owner has four horses. He usually ties these horses with 7 m long rope to pegs at each corner of a square-shaped grass field of 20 m length, to graze in his farm. But tying with rope sometimes results in injuries to his horses, so he decided to build a fence around the area so that each horse could graze. (CBSE 2024)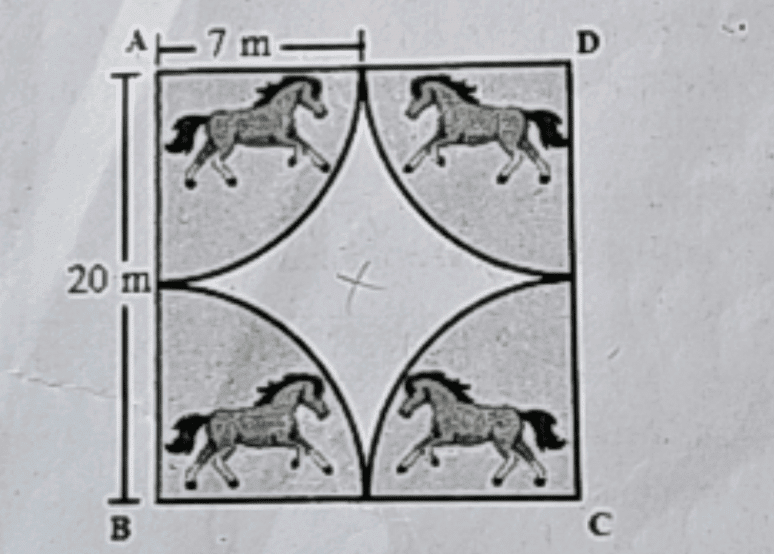
Based on the above, answer the following questions:
(A) Find the area of the square-shaped grass field.
(B) Find the area of the total field in which these horses can graze.
OR
If the length of the rope of each horse is increased from 7 m to 10 m, find the area grazed by one horse.
(Use π = 3.14)
(C) What is the area of the field that is left ungrazed if the length of the rope of each horse is 7 m?
 View Answer
View Answer 
Ans:
(A) Area of square shaped field
= 20 × 20
= 400 sq. m.
(B) Area of 4 quadrants
= Area of a circle of radius 7m = πr2
=4 × 14 × 227 × 7 × 7
= 154 m2
OR
New radius = 10 m
So, area grazed by one horse
= 14 (Area of circle with radius 10 m)
= 14 × π × (10)2
= 3.14 × 10 × 104
= 78.5 m2
(C) Area of ungrazed portion
= Area of square field - Area of circle with radius 7 m
= 20 × 20 - 227 × 7 × 7
= 400 - 154
= 246 m2
Previous Year Questions 2023
Q3: What is the area of a semi-circle of diameter 'd'? (CBSE, 2023)(a) 1/16πd2
(b) 1/4πd2
(c) 1/8πd2
(d) 1/2πd2
 View Answer
View Answer 
Ans: (c)
Given diameter of semi circle = d
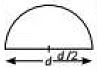
∴ Radius, r = d/2
Area of semi circle
= 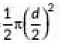
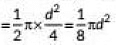
Q4: Case Study: The Governing council of a local public development authority of Dehradun decided to build an adventurous playground on the top of a bill, which will have adequate space for parking.
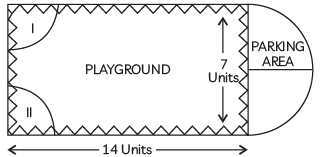
After the survey, it was decided to build a rectangular playground with a semi-circular area allotted for parking at one end of the playground. The length and breadth of the rectangular playground are 14 units and 7 units, respectively. There are two quadrants of radius 2 units on one side for special seats. Based on the above information, answer the following questions:
(i) What is the total perimeter of the parking area?
(ii) What is the total area of parking and the two quadrants? (CBSE 2023)
 View Answer
View Answer 
Ans: (i) Length of play ground . AB = 14 units, Breadth of play ground. AD = 7 units
Radius of semi - circular part is 7/2 units
Total perimeter of parking area = πr + 2r
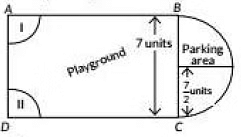
227 × 72 + 2 × 72
= 11 + 7 = 18 Units
(ii) Total area of parking and the two quadrants
= Area of semi-circular region + Area of 2 quadrants
= πR²2 + 2 × 14 × πr²
= π2 [ R² + r² ]
= 227 × 12 × (7/2)² + (2)²
= 117 × 49 + 44
= 117 × (49 + 16)4
= 117 × 654
= 71528
= 25.54 unit² (approx)
Q5: A chord of a circle of radius 14 cm subtends an angle of 60° at the centre. Find the area of the corresponding minor segment of the circle. Also, find the area of the major segment of the circle. (2023)
 View Answer
View Answer 
Ans: Here, radius t(r) = 14 cm and Sector angle (θ) = 60°
∴ Area of the sector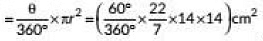
= 102.67 cm2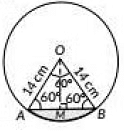
Since ∠O = 60° and OA = OB = 14 cm
∴ AOB is an equilateral triangle.
⇒ AS = 14 cm and ∠A = 60°
Draw OM ⊥ AB.
In ΔAMO
OMOA = sin60° = √32 ⇒ OM = OA × √32 = 14√32 cm = 7√3 cm
Now,
Area of △AOB = 12 × AB × OM
= 12 × 14 × 7√3 cm² = 49√3 cm²
= 49 × 1.732 cm² = 84.87 cm²
Now, area of the minor segment
= (Area of minor sector) - (Area of △AOB)
= 102.67 - 84.87 cm2
= 17.8 cm2
Area of the major segment
= Area of the circle - Area of the minor segment
= πr²1 - 17.8
= 227 × 14 × 14 - 17.8 cm2
= (616 - 17.8) cm2 = 598.2 cm2
Previous Year Questions 2022
Q6: The area swept by a 7 cm long minute band of a clock in 10 minutes is (CBSE 2022)
(a) 77 cm2
(b)
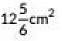
(c)
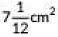
(d)
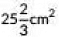
 View Answer
View Answer 
Ans: (d)
Angle formed by minute hand of a clock in 60 minutes = 360°
∴ Angle formed by minute hand of a clock in 10 minutes = 10/60 x 360° = 60°
Length of minute hand of a dock = radius = 7 cm
∴ Required area
= 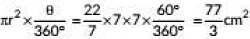
= 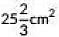
Q7: Given below is the picture of the Olympic rings made by taking five congruent circles of radius 1 cm each, intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1 cm. The total area of all the dotted regions assuming the thickness of the rings to be negligible is (2022)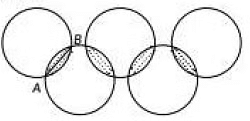
(a) 4 (π12) (√34) cm²
(b) (π6) - (√34) cm²
(c) 4 (π6) - (√34) cm²
(d) 8 (π6) - (√34) cm²
 View Answer
View Answer 
Ans: (d)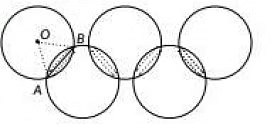
Let O be the centre of the circle. So. OA = OB = AB = 1 cm
So ΔOAB is an equilateral triangle.
∴ ∠AOB = 60°
∴ Required area = 8 x area of one segment with r = 1 cm,θ = 60°
= 8 x (area of sector - area of ΔAOB)
= 8 x ( θ360º x πr2 - √34a2)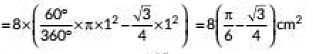
Previous Year Questions 2020
Q8: A piece of wire 22 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle. [Use π = 22/7] (2020) View Answer
View Answer 
Ans: Let AB be the wire of length 22 cm in the form of an art of a circle so blending an ∠AOB - 60° at centre O.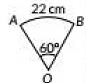
∵ Length of arc = 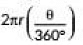
⇒ 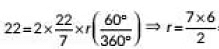
= 21 cm
Hence, radius of the circle is 21cm.
Q9: A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road. (CBSE 2020)
 View Answer
View Answer 
Ans:
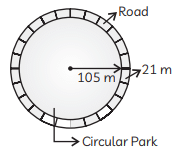
Given: Width of road = 21 m
Radius of park, r1 = 105 m
⇒ Radius of the whole circular portion (park + road)
r2 = 105 + 21 = 126 m
So, Area of road = Area of park and road - Area of park
= πr22 - πr12
= π (r22 - r12)
= 227 × [(126)2 - (105)2]
= 227 × (126 + 105) (126 - 105) [∵ a2 - b2 = (a + b)(a - b)]
= 227 × 231 × 21 = 15246
Hence, the area of the road is 15246 m2
Previous Year Questions 2019
Q10: A car has two wipers which do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle 120°. Find the total area cleaned at each sweep of the blades. (Take π = 22/7) (2019)
 View Answer
View Answer 
Ans: Here radius (r) = 21 cm
5ector angle (θ) = 120°
∴ Area cleaned by each sweep of the blades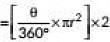 [∵ there are 2 blades]
[∵ there are 2 blades]
= 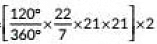
= 22 x 7 x 3 x 2 cm2
= 924 cm2
Q11: Find the area of the segment shown in the given figure, if the radius of the circle is 21 cm and ∠AOB = 120°. (Take π = 22/7) (2019)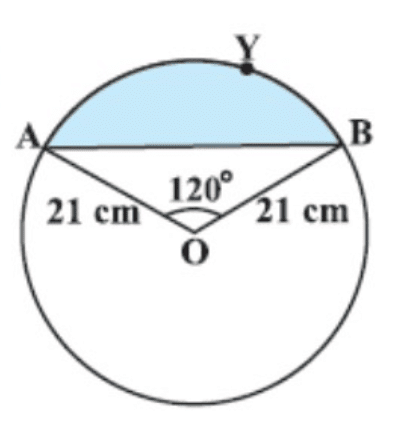
 View Answer
View Answer 
Ans: 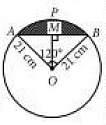
Draw OM ⊥ AB.
Area of the minor segment AMBP = Area of sector OAPB - Area of △AOB
Now, area of sector OAPB
= 120°360° × πr2
= 120°360° × 227 × 21 × 21
= 462 cm2
Since, OM ⊥ AB.
∠AOM = ∠BOM = 120°/2 = 60°
[∵ Perpendicular from the centre to the chord bisects the angle subtended by the chord at the centre.]
In △AOM,
sin 60° = AMAO , cos 60° = OMOA
= √32 = AM/21, 12 = OM/21
⇒ AM = 21√32 cm, OM = 212 cm
∴ AB = 2AM = 2 × 21√32 = 21√3 cm
Area of △AOB
= 12 × AB × OM
= 12 × 21√3 × 212
= 441√34 cm2
Hence, required area
= 462 - 441√34
= 462 - 381.92 = 80.08 cm2
Q12: In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region. (2019)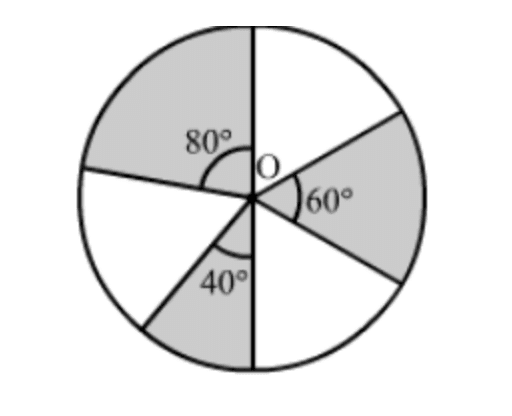
 View Answer
View Answer 
Ans: Radius (r) of circle = 7 cm
Area of shaded region =
π(7)2 × 40°360° + π(7)2 × 60°360° + π(7)2 × 80°360°
[∴ Area of sector = θ360° πr2]
= π(7)2 × 19 + π(7)2 × 16 + π(7)2 × 29
= π(7)2 [1/9 + 1/6 + 2/9]
= 227 × 7 × 7 × 918
= 77 cm2
Previous Year Questions 2017
Q13: A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of the circle. Find the area of major and minor segments of the circle. (Delhi 2017) View Answer
View Answer 
Ans: Radius of the circle = 10 cm
Central angle subtended by chord AB = 60°
Area of minor sector OACB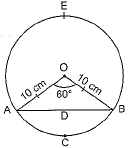
Area of equilateral triangle OAB formed by radii and chord
= √34 a² = √34 × (10)² = 1.7324 × 100 = 43.3 cm2
Area of minor segment ACBD
= Area of sector OACB - Area of triangle OAB
= (52.38 - 43.30) cm2
= 9.08 cm2
Area of circle
∴ Area of circle = πr²
= 227 × (10)² = 22 × 1007
= 314.28 cm2
Area of major segment ADBE
= Area of circle - Area of minor segment
= (314.28 - 9.08) cm2
= 305.20 cm2
Q14: In the given figure, ΔABC is a right-angled triangle in which ∠A is 90°. Semi-circles are drawn on AB, AC and BC as diameters. Find the area of the shaded region. (Al 2017)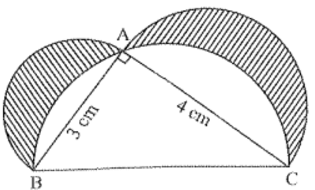
 View Answer
View Answer 
Ans: In right triangle ABC.
AB2 + AC2 = BC2
⇒ (3)2 + (4)2 = BC2 ⇒ 9 + 16 = BC2 ⇒ 25 = BC2
∴ BC = 5 cm
Now,
Area of shaded region = { ar(ΔABC) + ar(semicircle on side AB) + ar(semicircle on side AC) } - ar(semicircle on side BC)
Area of shaded region = [(12 × 3 × 4) + (12 π × (32) 2) + (12 π × (2)2)] - (12 π × (52) 2 cm2)
= 6 + 12 π 94 + 4 - 254 cm2
= 6 cm2
Hence, area of shaded region is 6 cm2
Q15: In the following figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. (CBSE (AI) 2017)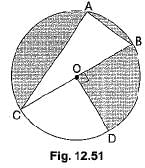
 View Answer
View Answer 
Ans: In right angle triangle ABC
Diameter BC = √(242 + 72) = 25 cm
Area ΔCAB = 12 × base × height
= 12 × 24 × 7 = 84 cm2
Area of shaded region = area of semicircle - area of ΔCAB + area of quadrant BOD
= π2 × (252) 2 - 84 + π4 × (252) 2
= (625π8) + (625π16) - 84
= (1875π16) - 84 = (117.18π - 84) = 283.94 cm2
Q16: Two circles touch internally. The sum of their areas is 116π cm2 and the distance between their centres is 6 cm. Find the radii of the circles. (CBSE 2017)
 View Answer
View Answer 
Ans: Let ‘r’ and ‘R’ be the radii of the smaller and bigger circles, respectively.
Then, OO’ = R – r = 6 cm [Given] ...(i)
Also, sum of their areas = 116π cm2
i.e., πR2 + πr2 = 116π
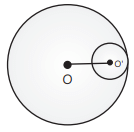 ⇒ R2 + r2 = 116 ...(ii)
⇒ R2 + r2 = 116 ...(ii)
We know, (R – r)2 = R2 + r2 – 2Rr
⇒ (6)2 = 116 – 2Rr
⇒ 2Rr = 116 – 36 = 80
⇒ Rr = 40 ...(iii)
Also, (R + r)2 = R2 + r2 + 2Rr = 116 + 2 × 40 [Using (ii) and (iii)]
⇒ (R + r)2 = 196
⇒ R + r = 14 ...(iv)
Now, adding equations (i) and (iv), we get
2R = 20
⇒ R = 10 cm
Putting the value of R in equation (i), we get
r = 4 cm
Hence, the radii of the bigger and smaller circles are 10 cm and 4 cm, respectively.
Previous Year Questions 2016
Q17: In Fig. 12.34, O is the centre of a circle such that diameter AB =13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take k = 3.14) (CBSE (AI) 2016)
 View Answer
View Answer 
Ans: In ΔABC, ∠ACB = 90° (Angle in the semicircle)
∴ BC2 + AC2 = AB2
∴ BC2 = AB2 -AC2
= 169 - 144 = 25
∴ BC = 5 cm
Area of the shaded region = area of semicircle - area of right ΔABC
= 12 πr2 - 12 × BC × AC
= 12 × (3.14) (132) 2 - 12 × 5 × 12
= 66.33 - 30 = 36.33 cm2
Q18: In the given figure, are shown two arcs PAQ and PBQ. Arc PAQ is a part of the circle with centre 0 and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with centre M.
If OP = PQ = 10 cm show that the area of the shaded region is 25 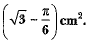 (CBSE (Delhi) 2016)
(CBSE (Delhi) 2016)
 View Answer
View Answer 
Ans: Since OP = PQ = QO
⇒ APOQ is an equilateral triangle
∴ ∠POQ = 60°
Area of segment PAQM
= θ360° πr2 - √34 a2
= 60°360° π × 102 - √34 × 102
= 100π6 - 100√34 cm2
Area of Semicircle with M as Centre
= π2 (5)2 = 25π2 cm2
Area of Shaded Region
= 25π2 - (50π3) - 25√3
= 25π2 - 503 π + 25√3
= -25π6 + 25√3
= 25(√3 - π6 ) cm2
Q19: In the figure, the boundary of the shaded region consists of four semicircular arcs, two smallest being equal. If the diameter of the largest is 14 cm and that of the smallest is 3.5 cm, calculate the area of the shaded region. Use π = 22/7 (Foreign 2016)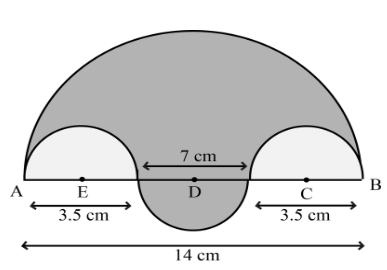
 View Answer
View Answer 
Ans: Given AD = 14 cm, AB = CD = 3.5 cm
∴ BC = 7 cm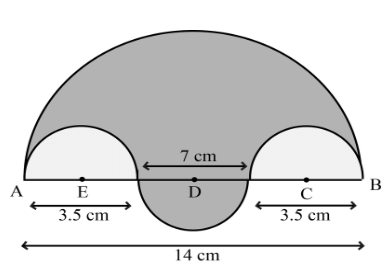


Substituting the Values 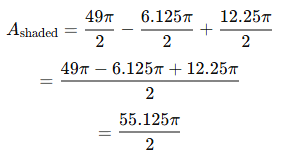
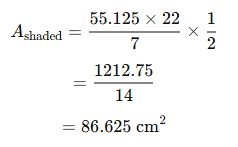
Q20: Find the area of the shaded region in Fig. 12.23, where a circular arc of radius 6 cm has been drawn with vertex 0 of an equilateral triangle ΔOAB of side 12 cm as the centre. (NCERT, CBSE (F) 2016)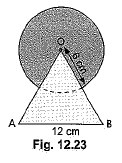
 View Answer
View Answer 
Ans:
Area of Shaded region = Area of equilateral triangle ABO + Area of Major sector
Area of Equilateral Triangle ABO = √34 × a2 = √34 × 12 × 12 cm2
= 62.352 cm2
Area of major sector = θ360 × π × r2
= 300360 × π × 6 × 6 cm2
= 94.2 cm2
Area of Shaded region = 62.352 + 94.2 = 156.55 cm2
Q21: An elastic belt is placed around the rim of a pulley of radius 5 cm. (Fig. 12.46). From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also, find the shaded area. (Use π = 3.14 and √3 = 1.73) (CBSE Delhi 2016)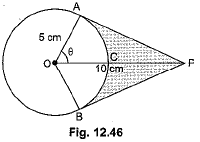
 View Answer
View Answer 
Ans: In △AOP, cos θ = 510
⇒ cos θ = 12 ⇒ θ = 60°
∴ Reflex ∠AOB = 240°
∴ Length of belt in contact with pulley = θ360° × 2πr
= 2 × 3.14 × 5 × 240360 = 20.93 cm
Now, APOA = tan 60°
PA = 5√3 cm = BP (Tangents from an external point are equal)
Area (△OAP + △OBP) = 2 × 12 × 5 × 5√3 = 25√3 = 43.25 cm2
Area of sector OACB = θ360° πr2 = 240360 × 3.14 × 25 = 26.17 cm2
Shaded area = 43.25 - 26.17 = 17.08 cm2
Q22: In the figure given, a sector OAP of a circle with centre O, containing angle θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of the shaded region is 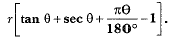 (CBSE (AI) 2016)
(CBSE (AI) 2016)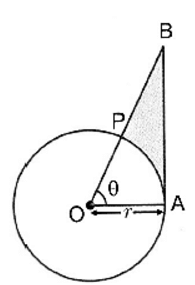
 View Answer
View Answer 
Ans:
Perimeter of shaded region = AB + PB + arc length AP ...(1)
Arc length AP = θ360 × 2πr = πθr180 ...(2)
In right-angled △OAB,
tan θ = ABr ⇒ AB = r tan θ ...(3)
sec θ = OBr ⇒ OB = r sec θ
OB = OP + PB
∴ r sec θ = r + PB
∴ PB = r sec θ - r ...(4)
Substitute (2), (3), and (4) in (1), we get:
Perimeter of shaded region = AB + PB + arc length AP
= r tan θ + r sec θ - r + πθr180
= r [tan θ + sec θ + πθ180 - 1]
Q23: In the figure, AB is a chord of a circle with a centre O and a radius of 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Also, find the area of the major segment ALBQA. (Use π = 3.14) (CBSE 2016)
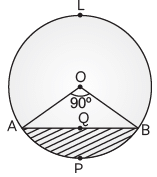
 View Answer
View Answer 
Ans: Given, A circle of radius (r) = 10 cm in which ∠AOB = 90º.
Area of the minor segment AQBP = Area of sector OAPB – Area of ΔAOB
= θ / 360° × πr2 – 1 /2 × OA × OB
= 90 / 360 ° × 3.14 × 10 × 10 – 1/ 2 × 10 × 10
= 3.14 × 5 × 5 – 5 × 10
= 78.5 – 50
= 28.5 cm2
So, Area of the minor segment AQBP = 28.5 cm2
Area of the major segment ALBQA = Area of circle – Area of minor segment AQBP
= 3.14 × (10)2 – 28.5
= 314 – 28.5
= 285.5 cm2
Area of major segment ALBQA = 285.5 cm2. Hence, the area of the minor segment AQBP is 28.5 cm2 and the area of the major segment ALBQA is 285.5 cm2.
Previous Year Questions 2015
Q24: In the figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region. (Foreign 2015) View Answer
View Answer 
Ans: Area of shaded region = area of trapezium - (area of 4 sectors)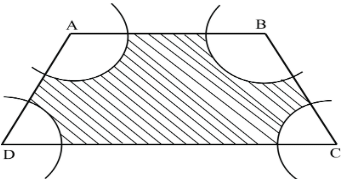
Area of trapezium = 12 (sum of parallel sides) × distance between parallel sides
= 12 (18 + 32) × 14 = 12 × 50 × 14 = 350 cm2 ...(i)
Area of sector on A = ∠A360° × π(7)2
Area of sector on B = ∠B360° × π(7)2
Area of sector on C = ∠C360° × π(7)2
Area of sector on D = ∠D360° × π(7)2
Total area of all sectors
= ∠A360° × π(7)2 + ∠B360° × π(7)2 + ∠C360° × π(7)2 + ∠D360° × π(7)2
= π360 (7)2(∠A + ∠B + ∠C + ∠D)
= 227 × 360 × 49 × 360° = 154 cm2 ...(ii) [Sum of angles of a quadrilateral is 360°]
From (i) and (ii),Area of shaded region = 350 - 154 = 196 cm2
|
127 videos|683 docs|84 tests
|
FAQs on Class 10 Maths Chapter 11 Previous Year Questions - Areas Related to Circles
| 1. What is the formula for the area of a circle? |  |
| 2. How do you calculate the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. How do you find the area of a sector of a circle? |  |
| 5. What are the properties of a circle that are important for solving problems in geometry? |  |






















