Class 10 Maths Chapter 11 Question Answers - Area Related to Circles
Q1: In a circular table cover of radius 70 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the figure. Find the total area of the design.
[Use √3 = 1.73 and π = 227 ]
Sol: ∵ Radius of the circle = 70 cm and O is the centre of the circle.
∴ OA = OB = OC
Since ∆ABC is an equilateral triangle,
∴∠ABO = ∠BOC= ∠CDA = 120°
Draw OD⊥BC
Now in right ΔBDO,
BDBO = sin 60° = √32
⇒ BD = BO × √32 = 70 × √32
= 35 √3 cm
Also BC = 2 × BD = 2 × 35 √3 = 70 √3 cm
∴ Area of equilateral ΔABC = √34 × (side)2
= √34 × (70 × √3)2
= √34 × 70 × 70 × 3 cm2
= √3 × 3 × 35 × 35 cm2 = 3675 √3 cm2
Also, area of the circle = πr2 = 227 × 70 × 70 cm2
= 22 × 10 × 70 cm2 = 15400 cm2
∴ Area of the shaded region= Area of Circle-Area of equilateral ΔABC
= 15400 cm2 − (3675√3) cm2
= 15400 cm2 − (3675 × 1.73) cm2
= 15400 cm2 − 6357.75 cm2 = 9042.25 cm2.
Q2: Calculate the area other than the area common between two quadrants of the circles of radius 16 cm each, which is shown as the shaded region in the figure.
Sol:
Area of sector ADB
= 90360 × 227 × 16 × 16 cm2 [using area = θ360 πr2 ]
= 14 × 227 × 16 × 16 cm2
= 22 × 4 × 167 cm2
= 14087 cm2
∴ Area of the shaded region-I = [Area of the square ABCD] − [Area of the sector ADB]
= 256 cm2 − 14087 cm2
= 1792 − 14087 cm2 = 3847 cm2
Similarly, area of the shaded region-II 384/7 cm2
∴ Total area of the shaded region = [Area of shaded region-I] + [Area of shaded region-II]
Q3: In the figure, PQ = 24 cm, PR = 7 cm and O is the centre of the circle. Find the area of shaded region. (Take π = 3.14)
Sol: In right Δ RPQ,
PR2 + PQ2 = RQ2
⇒ 72 + 242 = RQ2
⇒ 49 + 576 = RQ2
⇒ 625 = RQ2
⇒ Radius of semi-circle = 25/2 cm
∴ Area of semi-circle RQP
= 12 πr2 = 12 × 314100 × 252 × 252 cm2
= 1574 × 254 cm2 = 392516 cm2
= 245.31 cm2
Area of right ΔRPQ = 12 × RP × PQ
= 12 × 7 × 24 cm2 = 7 × 12 = 84 cm2
∴ Area of the shaded region=Area of semi-circle RQP − ar (right Δ RPQ)
=245.31 cm2 = 84 cm2 = 161.31 cm2.
Q4: The area of an equilateral triangle is 49√3. Taking each angular point as centre, circles are drawn with radius equal to half length of the side of the triangle. Find the area of triangle not included in the circles. [Take √3 = 1.73]
Sol: Let the given equilateral triangle be ABC, such that its side = 14 cm.
∴ Area of ΔABC:
= √34 × (side)2 = √34 × (14)2 cm2
= 1.734 × 14 × 14 cm2 = 49 × 1.73 cm2
= 84.77 cm2
Since each angle of an equilateral triangle = 60°,
∴ Area of a sector having θ as 60° and radius 14/2 i.e., 7 cm:
= 60360 × 227 × 7 × 7 cm2 = 11 × 73 cm2
[using area = θ360 πr2 ]
⇒ Area of 3 sectors = 3 × [11 × 7]3 cm2
= 77 cm2
∴ Area of the shaded region = [Area of equilateral ∆ ABC] − [Area of 3 sectors]
= 84.77 cm2 − 77 cm2 = 7.77 cm2.
Q5: Four equal circles are described at the four corners of the square so that each touches two of the others, the shaded area enclosed between the circles is 22/7 cm2 Find the radius of each circle.
Sol: Let 'r' cm be the radius of each circle.
∴ side of the square = 2r
Now, area of shaded region:
= [Area of the square] − [Area of 4 sectors]
= (2r)2 − 4 × 14 πr2
= 4r2 − πr2 = r2 (4 − π)
But the area of shaded region = 247 cm2
⇒ r2 (4 − π) = 247
⇒ r2 (28 − 22)7 = 247
⇒ r2 67 = 247 × 76 = 4
∴ r2 = 4 ⇒ r = ±2
But r cannot be − ve, so r = 2 cm
Q6: A square OABC is inscribed in a quadrant OABQ of a circle as shown in the figure. If OA = 14 cm, find the area of the shaded region. [use π = 22/7]
Sol: OABC is a square with side = 14 cm.
∴ Area of the square OABC = 14 cm × 14 cm = 196 cm2
Now, the diagonal of the square OABC:
OB = √(OA2 + AB2) = √(142 + 142)
= 14√2 cm
⇒ Radius of the quadrant OPBQ = 14√2 cm
∴ Area of the quadrant OABQ:
= 14 πr2 = 14 × 227 × (14 × √2)2 cm2
= 117 × 142 × 14 × 2 cm2
= 112 × 14 × 14 × 2 cm2
= 11 × 14 × 2 cm2 = 308 cm2
∴ Area of the shaded region
= 308 cm2 − 196 cm2 = 112 cm2.
Q7: In the figure, ABDC is a quadrant of a circle of radius 14 cm and a semi-circle is drawn with diameter BC. Find the area of the shaded region.
Sol: We have, in the right Δ ABC,
BC2 = AB2 + AC2 = 142 + 142 = 2 (14)2
⇒ BC = 14√2 cm
∴ Radius of the semi-circle = BC2 = 142 √2 = 7√2 cm
∴ Area of semi-circle BEC:
= 12 × 227 × (7√2)2 cm2 = 12 × 227 × 7 × 7 × 2 cm2
= 154 cm2
Area of the quadrant with radius 14 cm:
= 14 × 227 × 14 × 14 cm2 = 154 cm2
Area of right ΔABC:
= 12 × 14 × 14 cm2 = 98 cm2
Area of the shaded region:
= [Area of semi-circle with diameter BC] + [Area of ΔABC] − [Area of quadrant ABDC]
= 154 cm2 + 98 cm2 − 154 cm2 = 98 cm2.
Q8: In the figure, find the perimeter of the shaded region where, ADC, AEB and BFC are semicircles on diameters AC, AB and BC respectively.
Sol: Diameter of semi-circle ADC
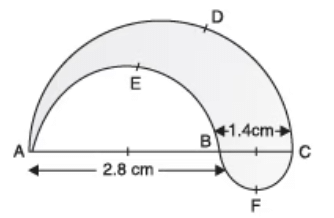
= 2.8 cm + 1.4 cm = 4.2 cm
⇒ Radius of semi-circle ADC = 4.22 cm = 2.1 cm
∴ Circumference of semi-circle ADC:
= 22 × 227 × 2.1 cm
= 22 × 227 × 2110 = 6610 cm = 6.6 cm
Diameter of semi-circle AEB = 2.8 cm
⇒ Radius of semi-circle AEB = 2.82 cm = 1.4 cm
∴ Circumference of semi-circle AEB:
= 22 × π × r = 22 × 227 × 1.4 cm
= 2210 cm = 4.4 cm
Diameter of semi-circle BFC = 1.4 cm
⇒ Radius of semi-circle BFC = 0.7 cm
∴ Circumference of semi-circle BFC
= 22 × 227 × 0.7cm = 2.2 cm
∴ Total perimeter of the shaded region = 6.6 cm + 4.4 cm + 2.2 cm = 13.2 cm.
Q9: In the figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region.
[use π = 3.14]
Sol. ∵ ΔABC is an equilateral triangle.
∴∠A = ∠B = ∠C = 60°
Area of sector AFEA:
= θ360 × πr2 cm2
= 60360 × π(5)2 cm2
∴ AF = 12 AB = 12 × 10 = 5 cm
= 16 × 3.14 × 5 × 5 cm2
= 78.56 cm2
Area of all the three sectors:
= 3 × 78.56 cm2 = 39.25 cm2
Thus, area of the shaded region = 39.25 cm2.
Q10: In figure OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region. [Use π = 22/7]
Sol: We have, the centre of the circle as ‘O’ and radius (r) = 7 cm
Area of the quadrant OABC = 14 πr2
= 14 × 227 × 7 × 7 cm2 = 112 × 7 cm2 = 772 cm2
Now, the area of ΔCOD:
= 12 × OC × OD
= 12 × 7 × 4 cm2 = 7 × 2 = 14 cm2
∴ Area of the shaded region = (Area of the quadrant OABC) − (Area of ΔCOD)
= 772 − 14 cm2 = 77 − 282 cm2 = 492 cm2
= 24.5 cm2
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 11 Question Answers - Area Related to Circles
| 1. What is the formula for calculating the area of a circle? |  |
| 2. How do you find the radius of a circle if you know its area? |  |
| 3. What is the difference between the radius and diameter of a circle? |  |
| 4. How can you calculate the circumference of a circle? |  |
| 5. What are the units used for measuring the area of a circle? |  |

















