Class 10 Maths Chapter 11 Question Answers - Surface Areas and Volumes
Q1: A sphere of diameter 6cm is dropped in a right circular cylindrical vessel partly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?

Ans: Let the water level raised in cylindrical vessel be 'h' cm
Since the water raised in the form of a cylinder
∵ The volume of the raised water = π (6)2 h
Now,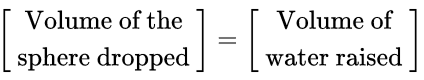
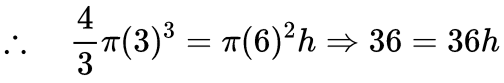
or h = 1 cm
Thus, the water level is raised by 1 cm
Q2: The figure shows a decorative block that is made of two solids—a cube and a hemisphere. The base of the block is a cube with edge 5 cm and the hemisphere, fixed on the top, has a diameter of 4.2 cm.
Find the total surface area of the block. [Take π = 22/7]

Ans: ∵ Total surface area of a cube = = 6 × (side)2
∴ Total surface area of the cubical block
= 6 × (5)2 − [Base area of the hemisphere]
= 150 − πr2
Now, total surface area of the solid
= 150 − πr2 + 2πr2 = 150 + πr2
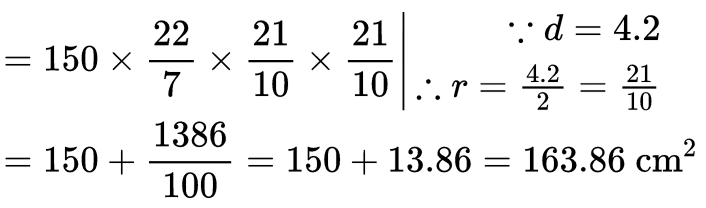
Q3: A toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the base of the conical portion is 7 cm and the total height of the toy is 14.5 cm. Find the volume of the toy. [Use π = 22/7]

Ans: 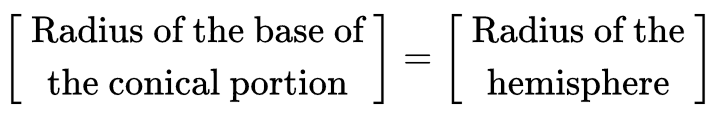
⇒ r = 3.5 cm,
Height of the conical portion (h) = 14.5 − 3.5 = 11 cm
Now, Volume of the toy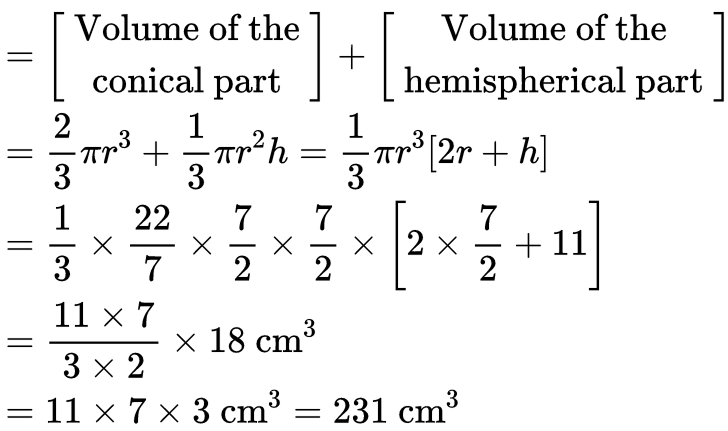
Q4: In the figure, the shape of a solid copper piece (made of two pieces) with dimensions as shown. The face ABCDEFA has a uniform cross-section. Assume that the angles at A, B, C, D, E and F are right angles. Calculate the volume of the piece.

Ans: Since, volume of a cuboid = lbh
∴ Volume of horizontal piece
= 22 × (8 + 2) × 3 cm3 = 22 × 10 × 3 cm3
= 660 cm3 Volume of the vertical piece
= 22 × 2 × 5 cm3 = 220 cm3
∴Total volume of the piece
= 660 cm3 + 220 cm3 = 880 cm3
Q5: A toy is in the form of a cone mounted on a hemisphere of a common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy. [Use π = 22/7]
Ans: Height of the cone, h = 31 − 7 = 24 cm
Radius of the cone = Radius of the hemisphere
r = 7 cm.
Now, Slant height, l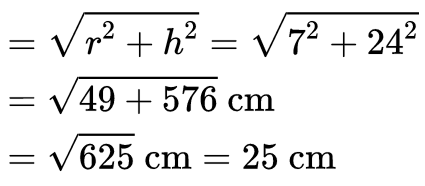 ∴ Total surface area of the toy
∴ Total surface area of the toy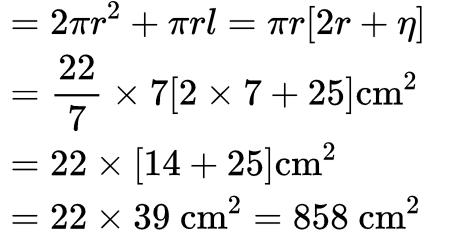
Q6: A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing at a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired?
Ans: The volume of water flows in the canal in one hour = width of the canal × depth of the canal × speed of the canal water = 3 × 1.2 × 20 × 1000 m3 = 72000 m3
In 20 minutes the volume of water = (72000 × 20)/ 60 = 24000 m3
Area irrigated in 20 minutes, if 8 cm, i.e., 0.08 m standing water is required
=24000/0.08 = 300000 m2 = 30 hectares
Q7: A right circular cone of radius 3 cm, has a curved surface area of 47.1 cm2. Find the volume of the cone, (use π = 3.14)
Ans: Radius of cone (r) = 3 cm
Curved Surface Area = πrl = 47.1 cm2 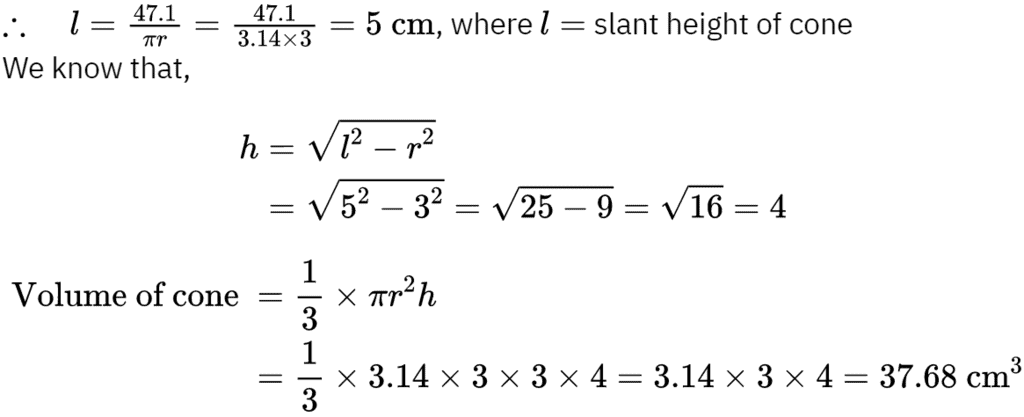
Q8: A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the toy. (use π =22/7)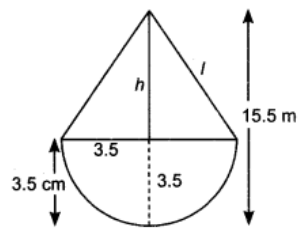
Ans: 
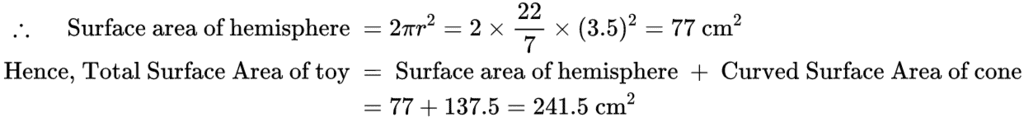
Q9: In figure, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at therate of rupees 500/sq. metre. (use π=22/7)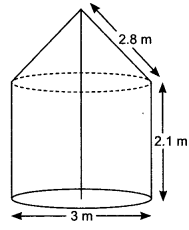
Ans: 
Q10: A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel.
Ans: 
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 11 Question Answers - Surface Areas and Volumes
| 1. What is the formula for finding the surface area of a cube? |  |
| 2. How do you find the surface area of a cylinder? |  |
| 3. What is the formula for finding the volume of a cone? |  |
| 4. How do you find the total surface area of a cuboid? |  |
| 5. How do you find the volume of a sphere? |  |

|
Explore Courses for Class 10 exam
|

|

















