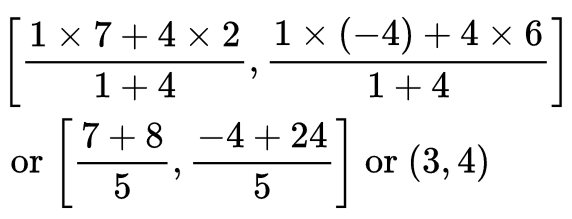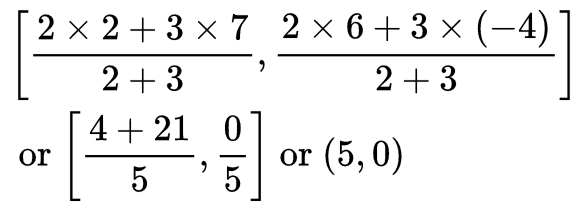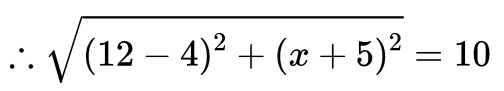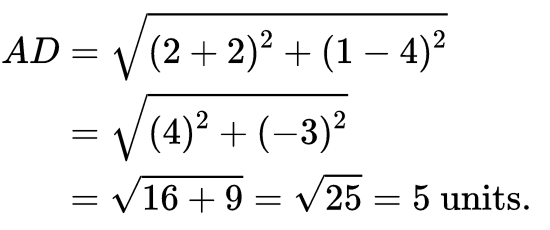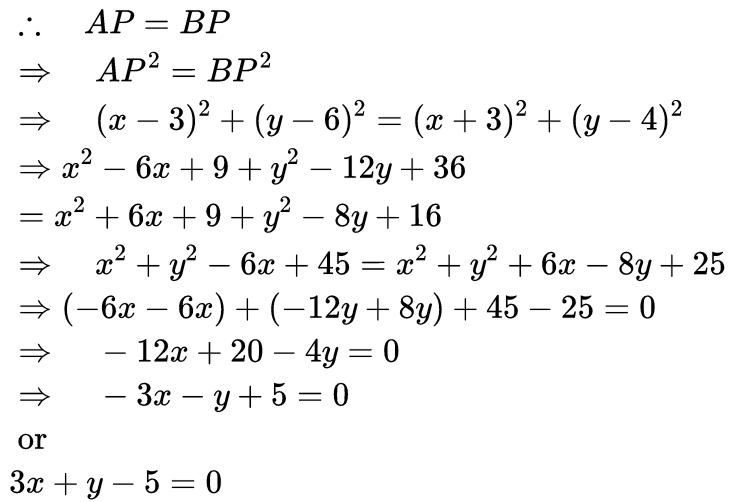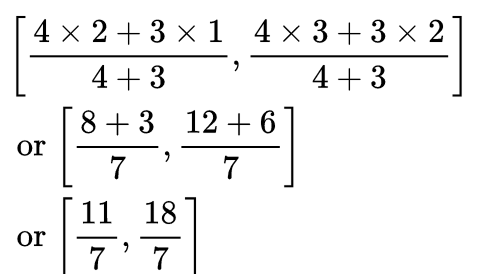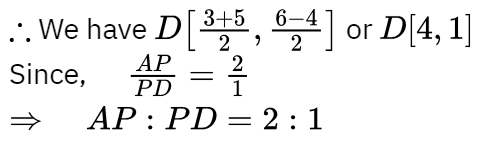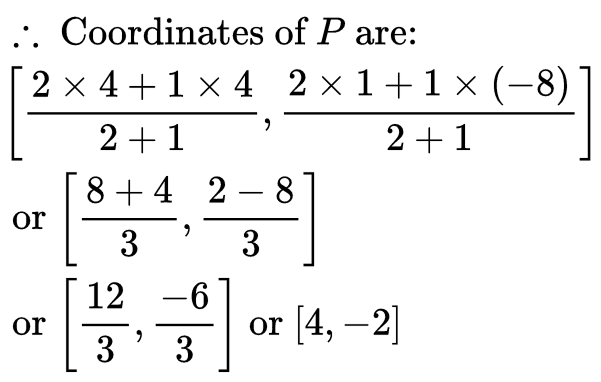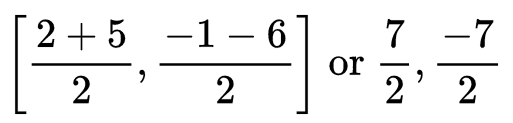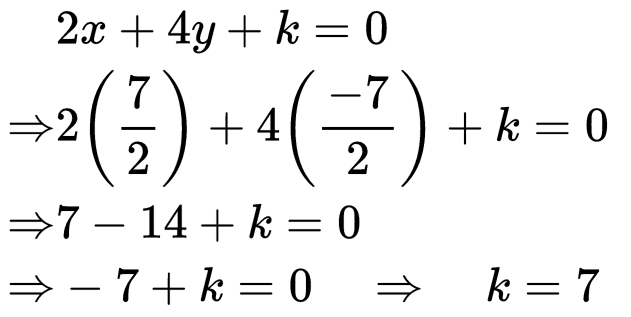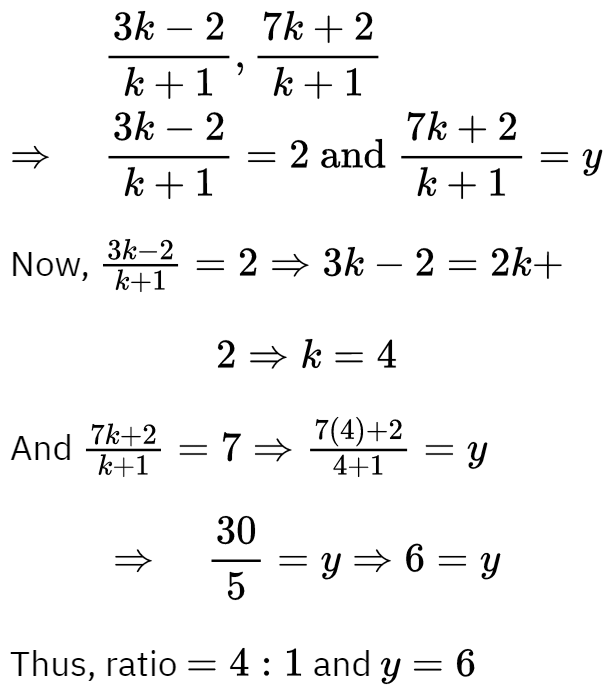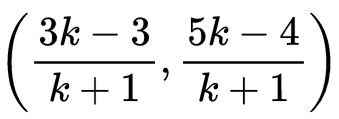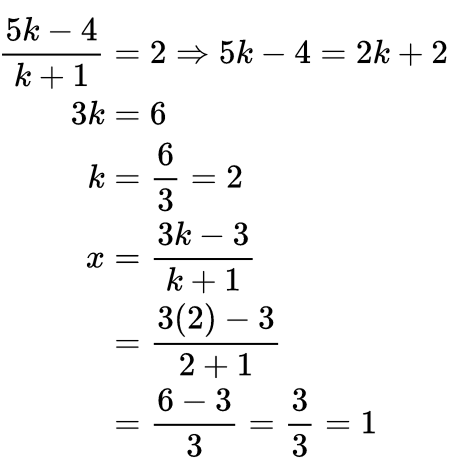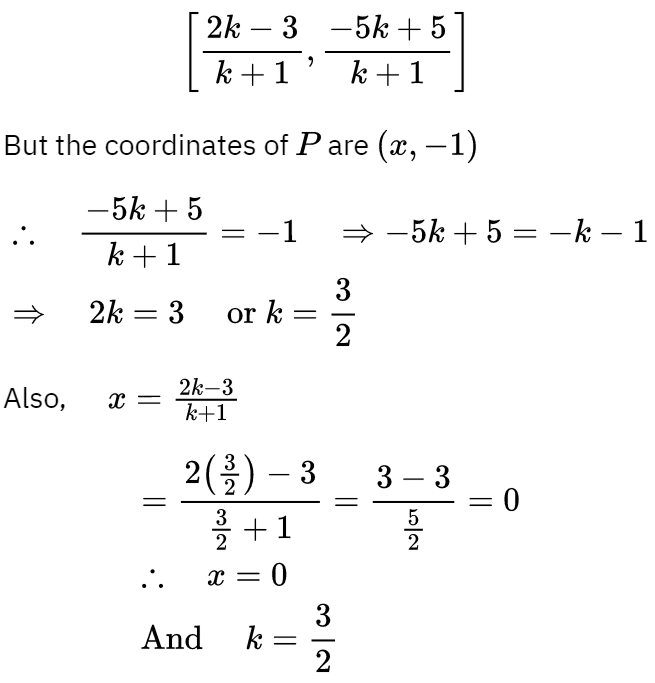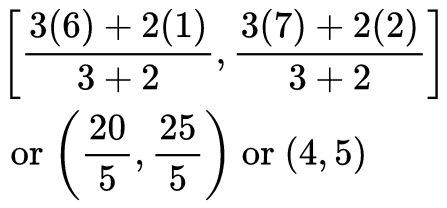Class 10 Maths Chapter 7 Question Answers - Coordinate Geometry - 1
Q1: Points P (5, − 3) is one of the two points of trisection of the line segment joining the points A (7, − 2) and B (1, − 5) near to A. Find the coordinates of the other point of trisection.
Ans:
∴ other point Q is the mid point of PB
Thus, the point Q is (3, − 4)
Q2: Points P, Q, R and S in this order, divide a line segment joining A(2, 6), B(7, − 4) in five equal parts. Find the coordinates of P and R.Ans:
∵ P, Q, R and S divide AB in five equal parts.
∴ AP = PQ = QR = RS = SB
Now, P divides AB in the ratio 1 : 4
∴ Coordinates of P are:
Again, R divides AB in the ratio 3 : 2
∴ Coordinates of R are:
Q3: Find the point on y-axis which is equidistant from the points (5, − 2) and (− 3, 2).
Ans: Let the required point be P (0, y) ä The given points are A (5, − 2) and B (− 3, 2)
∴ PA = PB
⇒ PA2 = PB2
∴(5 − 0)2 + (− 2 − y)2 =(− 3 − 0)2 + (2 − y)2
⇒ 52 + (− 2 − y)2 = (− 3)2 + (2 − y)2
⇒ 25 + 4 + y2 + 4y = 9 + 4 + y2 − 4y
⇒ 25 + 4y = 9 − 4y
⇒ 8 y = − 16 ⇒ y = − 2Thus, the required point is (0, − 2)
Q4: Find the point on y-axis which is equidistant from (− 5, 2) and (9, − 2).
Ans: Let the required point on Y-axis be P (0, y).The given points are A (− 5, 2) and B (9, − 2)
∴ AP = BP
⇒ − 4y − 4y = 81 + 4 − 4 − 25
⇒ − 8y =56⇒
∴ The required point = (0, −7)
Q5: Find the value of x for which the distance between the points P (4, − 5) and Q (12, x) is 10 units.
Ans: The given points are P (4 − 5) and Q (12, x) such that PQ = 10
⇒ (12 − 4)2 + (x + 5)2 =102
⇒ 82 + (x + 5)2 = 100
⇒ 64 + x2 + 25 + 10x = 100
⇒ x2 + 10x − 11 = 0
⇒ (x − 1) (x + 11) = 0
⇒ x = 1 or x = −11
Q6: If A (− 2, 4), B (0, 0) and C (4, 2) are the vertices of Δ ABC, then find the length of the median through the vertex A.
Ans: ∵ AD is the median on BC
∴ D is the mid-point of BC.
⇒ Coordinates of D are:
Now, the length of the median
Q7: If the points A (4, 3) and B (x, 5) are on the circle with the centre O (2, 3), find the value of x.
Ans: Let O (2, 3) be the centre of the circle.
∴ OA = OB ⇒ OA2 = OB2
⇒ (4 − 2)2 + (3 − 3)2 =(x − 2)2 + (5 − 3)2
⇒ 22 =(x − 2)2 + 22
⇒ (x − 2)2 = 0
⇒ x −2 = 0
⇒ x = 2Thus, the required value of x is 2.
Q8: Find the ratio in which the line 3x + 4y − 9 = 0 divides the line segment joining the points (1, 3) and (2, 7).
Ans: Let the ratio be k : 1.
⇒ 6k + 3 + 28k + 12 − 9k + 9 = 0
⇒ (6k + 28k − 9k) + (3 + 12 − 9) = 0
⇒ 25k + 6 = 0⇒
∴ The required ratio is − 6 : 25 or 6 : 25
Q9: If the point P (x, y) is equidistant from the points A (3, 6) and B (− 3, 4), prove that 3x+ y−5 = 0.
Ans:
∵ P is equidistant from A and B.
Q10: The coordinates of A and B are (1, 2) and (2, 3). If P lies on AB, then find the coordinates of P such that:
Ans:
Q11: If A (4, − 8), B (3, 6) and C (5, − 4) are the vertices of a Δ ABC, D(4, 1) is the mid-point of BC and P is a point on AD joined such that AP/PD = 2 , find the coordinates of P.
Ans: ∵ D is the mid-point of B
Q12: Show that the triangle PQR formed by the points
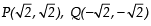
and is an equilateral triangle.
OR
Name the type of triangle PQR formed by the pointsand
Ans:
∴ PQ =
Q13: The line joining the points (2, − 1) and (5, − 6) is bisected at P. If P lies on the line 2x + 4y + k = 0, find the value of k.
Ans: We have A (2, − 1) and B (5, − 6).
∵ P is the mid point of AB,
∴ Coordinates of P are:Since P lies on the line 2x + 4y + k = 0
∴ We have:
Q14: Find the point on y-axis which is equidistant from the points (5, − 2) and (− 3, 2).
Ans: ∵ Let P is on the y-axis
∴ Coordinates of P are: (0, y)
Since, PA = PB
∴ PA2 = PB2
⇒ (5 - 0)2 + (-2 -y)2 = (-3 -0)2 + (2 - y)2
⇒ 25 + 4 + 4y + y2 = 9 + 4 - 4y + y2
⇒ 25 + 4y = 9 - 4y
⇒ 8y = -16
⇒ y = -16/8 = -2∴ The required point is (0, -2).
Q15: The line joining the points (2, 1) and (5, − 8) is trisected at the points P and Q. If point P lies on the line 2x − y + k = 0, find the value of k.
Ans:
Q16: Find the point on x-axis which is equidistant from the points (2, − 5) and (− 2, 9).
Ans: ∵ The required point ‘P’ is on x-axis.
∴ Coordinates of P are (x, 0).
∴ We haveAP = PB
⇒ AP2 = PB2
⇒ (2 − x)2 + (− 5 + 0)2 =(− 2 − x)2 + (9 − 0)2
⇒ 4 − 4x + x2 + 25 = 4 + 4x + x2 + 81
⇒ 4x + 25 = 4x + 81
⇒ − 8x = 56
∴ The required point is (−7, 0).
Q17: The line segment joining the points P (3, 3) and Q (6, − 6) is trisected at the points A and B such that A is nearer to P. It also lies on the line given by 2x + y + k = 0. Find the value of k.
Ans: ∵ PQ is trisected by A such that
Q18: Find the ratio in which the points (2, 4) divides the line segment joining the points A (− 2, 2) and B (3, 7). Also find the value of y.
Ans: Let P (2, y) divides the join of A (− 2, 2) and B (3, 7) in the ratio k:1
∴ Coordinates of P are:
Q19: Find the ratio in which the point (x, 2) divides the line segment joining the points (− 3, − 4) and (3, 5). Also find the value of x.
Ans: Let the required ratio = k : 1
∴ Coordinates of the point P are:
But the coordinates of P are (x, 2)
Q20: If P (9a – 2, –b) divides the line segment joining A (3a + 1, −3 ) and B (8a, 5) in the ratio 3 : 1, find the values of a and b.
Ans: ∵ P divides AB in the ratio 3 : 1
∴ Using the section formula, we have:
− b = 3 or b = −3
⇒ 36a − 8= 27a + 1 and b= −3
⇒ 9a = 9 and b = −3
Thus, the required value of a = 1 and b = −3
Q21: Find the ratio in which the point (x, − 1) divides the line segment joining the points (− 3, 5) and (2, − 5). Also find the value of x.
Ans: Let the required ratio is k : 1
Q22: Find the co-ordinates of the points which divide the line segment joining A(2, −3) and B(−4, −6) into three equal parts.
Ans: Let the required points are P(x1, y1) and Q(x2, y2)
∴ Using section formula, we have:
Thus, the coordinates of the required points are (0, −4) and (−2, 5)
Q23: If the mid-point of the line segment joining the point A(3, 4) and B(k, 6) is P(x, y) and x + y – 10 = 0, then find the value of k.
Ans: ∵ Mid point of the line segment joining A(3, 4) and B(k, 6)
Q24: Point P, Q, R and S divide the line segment joining the points A (1, 2) and B (6, 7) in 5 equal parts. Find the co-ordinates of the points P, Q and R.
∴ P, Q, R and S, divide AB into five equal parts.
∴ AP = PQ = QR = RS = SB
Now, P divides AB in the ratio 1 : 4
Let, the co-ordinates of P be x and y.
∴ Using the section formula i.e.,Next, Q divides AB in the ratio 2 : 3
∴ Co-ordinates of Q are:Now, R divides AB in the ratio 3 : 2
⇒ Co-ordinates of R are:The co-ordinates of P, Q and R are respectively:(2, 3), (3, 4) and (4, 5).
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 7 Question Answers - Coordinate Geometry - 1
| 1. What is the distance formula in coordinate geometry? |  |
| 2. How do you find the midpoint between two points? |  |
| 3. What is the slope of a line and how is it calculated? |  |
| 4. What is the equation of a line in slope-intercept form? |  |
| 5. How do you determine if three points are collinear? |  |