Class 10 Maths Previous Year Questions - Coordinate Geometry
Previous Year Questions 2025
Q1: The distance of the point (4, 0) from x-axis is:
(a) 4 units
(b) 16 units
(c) 0 units
(d) 4√2 units
 View Answer
View Answer 
Ans: (c)
Distance of point (4, 0) from x-axis is 0 units.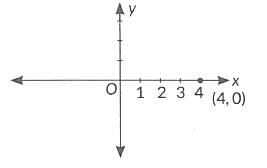
Q2: The distance of the point A(-3, -4) from x-axis is
(a) 3
(b) 4
(c) 5
(d) 7
 View Answer
View Answer 
Ans: (b)
Distance of the point A(-3, -4) from x-axis = absolute value of the ordinate = 4 units.
Q3: AOBC is a rectangle whose three vertices are A(0, 2), B(0, 0) and 8(4, 0). The square of the length of its diagonal is equal to:
(a) 36
(b) 20
(c) 16
(d) 4
 View Answer
View Answer 
Ans: (b)
In rectangle AOBC, AB is the diagonal, where A(0, 2) and B(4, 0).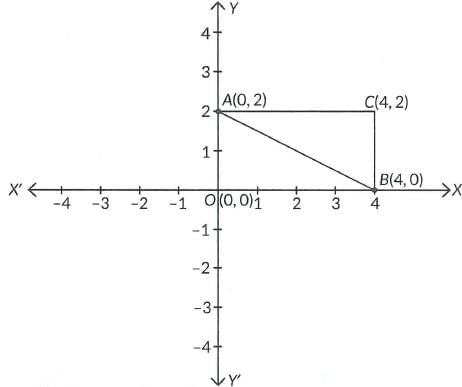 ∴ By distance formula,
∴ By distance formula,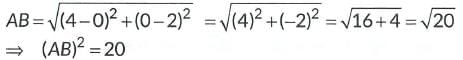
Q4: The coordinates of the centre of a circle are (2a, a - 7). Find the value(s) of 'a' if the circle passes through the point (11, -9) and has diameter 10√2 units.
 View Answer
View Answer 
Ans: 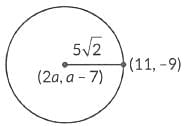 Given, diameter
Given, diameter 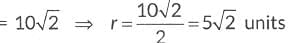
Since, circle passes through (11, -9)
∴ Using distance formula, we have
(11 - 2a)2 + (-9 - a + 7)2 = (5√2)2
⇒ 121 + 4a2 - 44a + a2 + 4 + 4a = 50
⇒ 5a² - 40a + 125 - 50 = 0
⇒ 5a² - 40a + 75 = 0
⇒ a² - 8a + 15 = 0
⇒ a² - 3a - 5a + 15 = 0
a(a - 3) - 5(a - 3) = 0
⇒ (a - 3)(a - 5) = 0 ⇒ a = 3 or 5
Q5: Prove that abscissa of a point P which is equidistant from points with coordinates A(7, 1) and 8(3, 5) is 2 more than its ordinate.
 View Answer
View Answer 
Ans: Let the point P be (x, y).
Since, P is equidistant from A(7, 1) and 8(3, 5), we get PA = PB
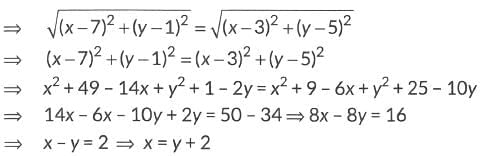
Hence, abscissa of point P is 2 more than its ordinate.
Q6: If the mid-point of the line segment joining the points (a, 4) and (2, 2b) is (2, 6), then the value of (a+ b) is given by:
(a) 6
(b) 7
(c) 8
(d) 16
 View Answer
View Answer 
Ans: (a)
Let the coordinates be A(a, 4), B(2, 2b) and C(2, 6) respectively. 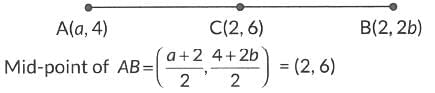
On comparing the coordinates, we get 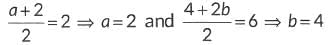
∴ a + b = 2 + 4 = 6
Q7: Two of the vertices of ΔPQR are P(-1, 5) and Q(5, 2). The coordinates of a point which divides PQ in the ratio 2 : 1 are:
(a) (3, -3)
(b) (5, 5)
(c) (3,3)
(d) (5, 1)
 View Answer
View Answer 
Ans: (c)
Let (x, y) be the coordinates of a point that divides P(-1, 5) and Q(5, 2) in the ratio 2:1.
By section formula, 
∴ Required coordinates are (3, 3).
Q8: The line represented by 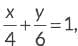 intersects x-axis and y-axis respectively at P and Q. The coordinates of the mid-point of line segment PQ are:
intersects x-axis and y-axis respectively at P and Q. The coordinates of the mid-point of line segment PQ are:
(a) (2, 3)
(b) (3, 2)
(c) (2, 0)
(d) (0, 3)
 View Answer
View Answer 
Ans: (a) 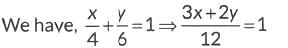
⇒ 3x + 2y = 12 ... (i)
Put x = 0 in (i), we have 3(0) + 2y = 12 ⇒ y = 12/2 = 6
Coordinates of Q are (0, 6).
Put y = 0 in (i), we have 3x + 2(0) = 12 
∴ Coordinates of P are (4, 0)
∴ Coordinates of mid point of PQ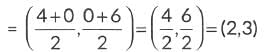
Q9: The mid-point of the line segment joining the points P(-4, 5) and Q(4, 6) lies on:
(a) x-axis
(b) y-axis
(c) origin
(d) neither x-axis nor y-axis
 View Answer
View Answer 
Ans: (b)
Mid-point of PQ 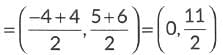
Here, x-coordinate is zero.
So, mid-point lies on y-axis.
Q10: If the mid-point of the line segment joining the points A(3, 4) and B(k, 6) is P(x, y) and x + y - 10 = 0, find the value of k.
 View Answer
View Answer 
Ans: By mid point formula 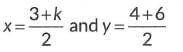
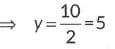
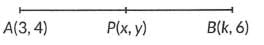
Now, put y = 5, in x + y - 10 = 0, we have
⇒ x + 5 - 10 = 0⇒ x=5 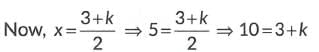
⇒ k = 10 - 3 = 7
Q11: Find the coordinates of the points which divide the line segment joining A(-2, 2) and B(2, 8) into four equal parts.
 View Answer
View Answer 
Ans: Let P, Q and R divides the line joining AB into four equal parts.
Now, point P divides the line segment AB in 1 : 3. 
∴ The coordinates of P are given by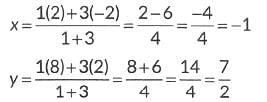
∴ The coordinates of P are 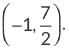
Point Q divides the line segment in 1:1 i.e., Q is mid point of AB. 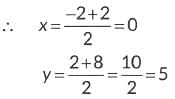
∴ The coordinates of Q are (0, 5).
Point R divides AB in 3 : 1
The coordinates of R are given by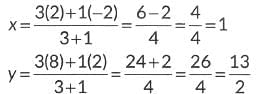
∴ The coordinates of R are 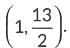
Q12: Find the ratio in which the y-axis divides the line segment joining the points (5, -6) and (-1, -4). Also find the point of intersection.
 View Answer
View Answer 
Ans: Let the point P(0, y) on y-axis divides the line segment joining the points A(5, -6) and B(-1, -4) in the ratio k : 1.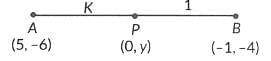
∴ By section formula, we have, 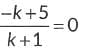
⇒ -k + 5 = 0 ⇒ k = 5 ... (i)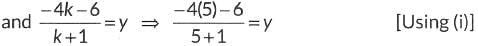
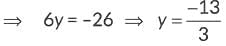
Hence, the required point is 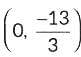 and the required ratio is 5 : 1.
and the required ratio is 5 : 1.
Q13: If the points A(6, 1), B(p, 2), C(9, 4) and 0(7, q) are the vertices of a parallelogram ABCD, then find the values of p and q. Hence, check whether ABCD is a rectangle or not.
 View Answer
View Answer 
Ans: Since, ABCD be a parallelogram.
∴ Mid-point of AC = Mid-point of BO 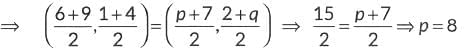
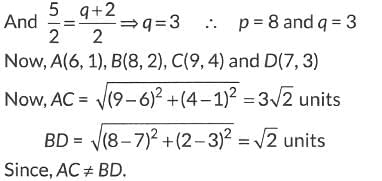
Thus, it is not a rectangle.
Previous Year Questions 2024
Q1: Assertion (A): The point which divides the line segment joining the points A (1, 2) and B (–1, 1) internally in the ratio 1 : 2 is 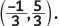
Reason (R): The coordinates of the point which divides the line segment joining the points A(x1, y1) and B(x2, y2) in the ratio m1 : m2 are 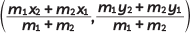 (1 Mark) (CBSE 2024)
(1 Mark) (CBSE 2024)
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
 View Answer
View Answer 
Ans: (d)
Assertion says that point ( -13 , 53 ) divides the line joining the points A(1,2) and B(-1,1) in 1:2.
∴ By section formula,
x = m1x2 + m2x1m1 + m2
= 1×(-1) + 2×13 = 13
y = m1y2 + m2y1m1 + m2
= 1×1 + 2×21+2
= 1 + 43
= 53
which is not equal to RHS i.e. 1/3
Q2: Find a relation between x and y such that the point P(x, y) is equidistant from the points A(7, 1) and B(3, 5). (3 Marks) (CBSE 2024)
 View Answer
View Answer 
Ans:
Since, P(x, y) is equidistant from A(7, 1) and B(3, 5)
So, PA = PB
⇒ PA2 = PB2
⇒ (x – 7)2 + (y – 1)2 = (x – 3)2 + (y – 5)2
⇒ x2 + 49 – 14x + y2 + 1 – 2y = x2 + 9 – 6x + y2 + 25 – 10y
⇒ 6x – 14x + 50 – 34 + 10y – 2y = 0
⇒ – 8x + 8y + 16 = 0
⇒ 8x – 8y – 16 = 0
⇒ 8(x – y – 2) = 0
⇒ x – y – 2 = 0
⇒ x – y = 2
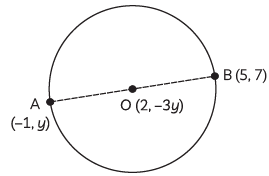
Q3: Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y) such that AB is a diameter of the circle. Find the value of y. Also, find the radius of the circle. (3 Marks) (CBSE 2024)
 View Answer
View Answer 
Ans: A (– 1, y); B(5, 7)
Since, AB is a diameter of circle and O is the centre of the circle.
OA = OB i.e., O divides AB in 1 : 1
So m1 : m2 = 1 : 1
So 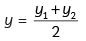
 ⇒
⇒ 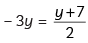
⇒ – 6y = y + 7
⇒ – 7y = 7
⇒ y = – 1
Point O = (2, 3), A = (–1, – 1)
Now,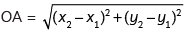
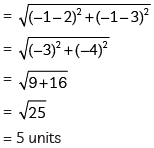
So, radius of circles = 5 units
Q4: Find the ratio in which the line segment joining the points (5, 3) and (–1, 6) is divided by Y-axis. (3 Marks) (CBSE 2024)
 View Answer
View Answer 
Ans:
If y-axis divides points (5, 3) and (–1, 6) then coordinate of that point will be (0, y). Let P(0, y) divides A(5, 3) and B(–1, 6) in k : 1.
m1 : m2 = k : 1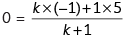
⇒ 0 × (k + 1) = – k + 5
⇒ 0 = – k + 5
⇒ k = 5
So, m1 : m2 = 5 : 1
Previous Year Questions 2023
Q1: The distance of the point (-1, 7) from the x-axis is (1 Mark) (2023)(a) -1
(b) 7
(c) 6
(d) √50 [2023, 1 Mark]
 View Answer
View Answer 
Ans: (b)
Distance from x-axis = y-coordinate of point = 7 units
Q2: Assertion (A): Point P(0, 2) is the point of intersection of the y-axis with the line 3x + 2y = 4. (1 Mark) (2023)
Reason (R): The distance of point P(0, 2) from the x-axis is 2 units.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
 View Answer
View Answer 
Ans: (b)
- Assertion (A):To find the intersection of the y-axis with the line 3x + 2y = 4, set x = 0:
3(0) + 2y = 4 ⇒ y = 2. So, the point of intersection is P(0,2).
Assertion (A) is true.
- Reason (R):The distance of point P(0,2) from the x-axis is indeed 2 units.
Reason (R) is true.
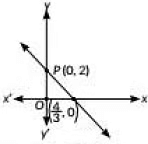
However, Reason (R) does not explain Assertion (A); it is just a separate true statement.
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
Q3: The distance of the point (-6, 8) from origin is (1 Mark) (2023)
(a) 6
(b) -6
(c) 8
(d) 10
 View Answer
View Answer 
Ans: (d)
Distance of the point (-6, 8) from origin (0, 0)
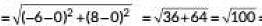
= 10 Units
Q4: The points (-4, 0), (4, 0) and (0, 3) are the vertices of a (1 Mark) (CBSE 2023)
(a) right triangle
(b) isosceles triangle
(c) equilateral triangle
(d) scalene triangle
 View Answer
View Answer 
Ans: (b)
The points be A(-4, 0), B(4, 0) and C(0, 3).
Using distance formula
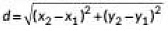
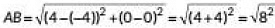
= 8 units
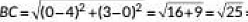
= 5 units
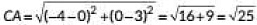
= 5 units
And, AB2 ≠ BC2 + CA2 [∵ BC = CA]
∴ ΔABC is an isosceles triangle.
Q5: The centre of a circle is (2a, a - 7). Find the values of 'a' if the circle passes through the point (11, -9). Radius of the circle is 5√2 cm. (3 Marks) (2023)
 View Answer
View Answer 
Ans: Given centre of a circle is(2a, a - 7 )
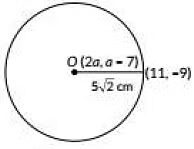
Radius of the circle is 5√2 cm.
∴ Distance between centre (2a, a - 7) and (11, - 9 ) = radius of circle.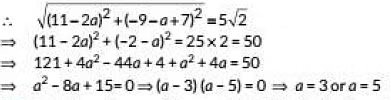
Q6: In what ratio, does the x-axis divide the line segment joining the points A(3, 6) and B(-12, -3) ? (1 Mark) (2023)
(a) 1 : 2
(b) 1 : 4
(c) 4 : 1
(d) 2 : 1
 View Answer
View Answer 
Ans: (d)
Let the point on the x-axis be (x, 0) which divides the line segment joining the points A(3, 6) and B(-12, -3) in the ratio k : 1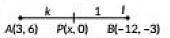
Using section formula, we have
(x, 0) = (-12)k + 3(1)k + 1 , (-3)k + 6(1)k + 1
⇒ -3k + 6k + 1 = 0
⇒ -3k + 6 = 0
⇒ k = 2
Hence, the required ratio is 2 : 1.
Q7: Case Study: Jagdish has a Field which is in the shape of a right angled triangle AQC. He wants to leave a space in the form of a square PQRS inside the field for growing wheat and the remaining for growing vegetables (as shown in the figure). In the field, there is a pole marked as O. (4/5/6 Marks) (CBSE 2023)
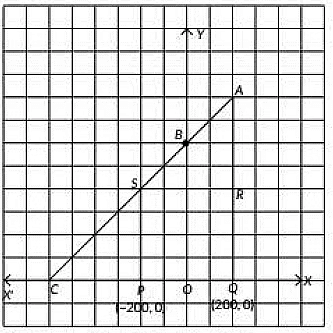
Based on the above information, answer the following questions:
(i) Taking O as origin, coordinates of P are (-200, 0) and of Q are (200, 0). PQRS being a square, what are the coordinates of R and S?
(ii) (a) What is the area of square PQRS?
(b) What is the length of diagonal PR in square PQRS?
(iii) If S divides CA in the ratio K: 1, what is the value of K, where point A is (200, 800)?
 View Answer
View Answer 
Ans: (i) We have. P = (-200, 0) and Q = (200, 0)
The coordinates of R and S are (200, 400) and (-200, 400).
(ii) (a) The length PQ = 200 + 200 = 400 units.
Area of square PQRS = 400 x 400 = 160000 sq. units.
(b) Length of diagonal PR = √2 x length of side = 400√2 units.
(iii) Here,
Using section formula, we have
∴ Kx2 + x1K + 1 , Ky2 + y1K + 1 = (-200, 400)
⇒ K(200) + (-600)K + 1 , K(800) + 0K + 1 = (-200, 400)
⇒ 200K - 600K + 1 , 800KK + 1 = (-200, 400)
∴ 800KK + 1 = 400
⇒ 800K = 400K + 400
⇒ 400K = 400
⇒ K = 1
Previous Year Questions 2022
Q1: The line represented by 4x - 3y = 9 intersects the y-axis at (2022)
(a) (0, -3)
(b) (9/4, 0)
(c) (-3, 0)
(d) (0, 9/4)
 View Answer
View Answer 
Ans: (a)
Given, the equation of line is 4x- 3y = 9.
Putting x = 0, we get 4x(0) - 3y = 9 ⇒ y = -3
So, the line 4x - 3y = 9 intersects the y-axis at (0, -3).
Q2: The point on x-axis equidistant from the points P(5, 0) and Q(-1, 0) is (2022)
(a) (2, 0)
(b) (-2, 0)
(c) (3, 0)
(d) (2, 2)
 View Answer
View Answer 
Ans: (a)
Let coordinates of the point on the x-axis be R (x, 0).
√((x - 5)² + (0 - 0)²) = √((x + 1)² + (0 - 0)²)
Simplify:
(x - 5)² = (x + 1)²
Expand:
x² - 10x + 25 = x² + 2x + 1
Solve for x:
-10x + 25 = 2x + 1
⇒ -12x = -24
⇒ x = 2
So, the point is (2, 0).
Q3: The x-coordinate of a point P is twice its y-coordinate. If P is equidistant front Q(2, -5) and R(-3, 6), then the coordinates of P are (2022)
(a) (8, 16)
(b) (10, 20)
(c) (20, 10)
(d) (16, 8)
 View Answer
View Answer 
Ans: (d)
Let coordinate of point P= t
So, .(x-coordinate of point P = 2t ∴ Point is P (2t, t).
Given, PQ = RP ⇒ PQ2 = RP2
⇒ (2t - 2)2 + (t + 5)2 = (2t + 3)2 + (t - 6)2 [By distance formula]
⇒ 4t2 - 8t + 4 + t2 + 10t + 25 = 4t2+ 12t + 9 + t2- 12t + 36
⇒ 2t = 16
t = 8
P = 2t = 2 x 8 = 16
Coordinates of P are (16, 8).
Q4: The ratio in which the point (-4, 6) divides the line segment joining the points A(-6, 10) and B(3, -8) is (2022)
(a) 2 : 5
(b) 7 : 2
(c) 2 : 7
(d) 5 : 2
 View Answer
View Answer 
Ans: (c)
Let point P(-4, 6) divides the line segment AB in the ratio m1: m2.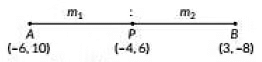
By section formula, we have
(-4,6) = 3m1 - 6m2m1 + m2 , -8m1 + 10m2m1 + m2
Now, -4 = 3m1 - 6m2m1 + m2
⇒ 3m1 - 6m2 = -4m1 - 4m2
⇒ 7m1 = 2m2 ∴ m1 : m2 = 2:7
Putting the value of m1 : m2 in the y-coordinate, we get
-8m1 +10m1 + m2 = -8 × 27 + 10
-167 + 10 = 6
Hence, the required ratio is 2:7.
Q5: Case Study: Shivani is an interior decorator. To design her own living room, she designed wail shelves. The graph of intersecting wail shelves is given below: (2022)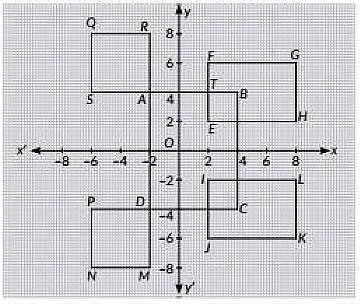
Based on the above information, answer the following questions:
(i) If O is the origin, then what are the coordinates of S?
(a) (-6, -4)
(b) (6, 4)
(c) (-6, 4)
(d) (6, -4)
 View Answer
View Answer 
Ans: (c)
Coordinates of S are (-6, 4).
(ii) The coordinates of the mid-point of the line segment joining D and H is
(a) 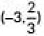
(b) (3, -1)
(c) (3, 1)
(d) 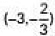
 View Answer
View Answer 
Ans: (b)
Coordinates of D are (-2, -4) and coordinates of H are (8, 2).
∴ Midpoint of DH = 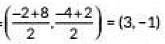
(iii) The ratio in which the x-axis divides the line-segment joining the points A and C is
(a) 2 : 3
(b) 2 : 1
(c) 1 : 2
(d) 1 : 1
 View Answer
View Answer 
Ans: (d)
Coordinates of A are (-2, 4) and coordinates of C are (4, -4).
Let (x, 0) divides the line segment joining the points A and C in the ratio m1 : m2
By section formula, we have
(x, 0) = 4m1 - 2m2m1 + m2 , -4m1 + 4m2m1 + m2
Now, 0 = -4m1 + 4m2m1 + m2
⇒ -4m1 + 4m2 = 0
⇒ m1 : m2 = 1:1
(iv) The distance between the points P and G is
(a) 16 units
(b) 3√74 units
(c) 2√74 units
(d) √74 units
 View Answer
View Answer 
Ans: (c)
Coordinates of P are (-6, -4) and coordinates of G are (8, 6).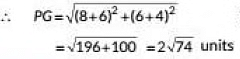
(v) The coordinates of the vertices of rectangle IJKL are
(a) I(2, 0), J(2, 6), K(8,6), L(8, 2)
(b) I(2, -2), J(2, -6), K(8, - 6), L(8, -2)
(c) I(-2, 0), J(-2, 6), K(-8, 6), L(-8, 2)
(d) I(-2, 0), J(-2, -6), K(-8, -6), L(-8, -2)
 View Answer
View Answer 
Ans: (b)
Coordinates of vertices of rectangle IJKL are respectively I(2, -2), J(2, -6), K(8, -6),L(8, -2).
Previous Year Questions 2021
Q1: Case Study : Students of a school are standing in rows and columns in their school playground to celebrate their annual sports day. A, B, C and D are the positions of four students as shown in the figure. (2021)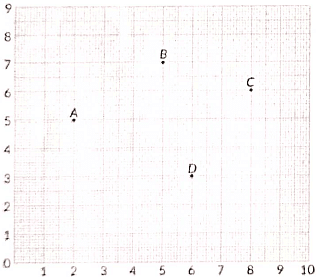
Based on the above, answer the following questions:
(i) The figure formed by the four points A, B, C and D is a
(a) square
(b) parallelogram
(c) rhombus
(d) quadrilateral
 View Answer
View Answer 
Ans: (d)
From figure coordinates are A(2, 5), B(5, 7), C(8, 6) and D(6, 3)
Now, 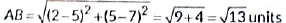
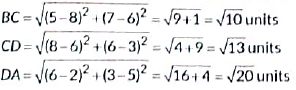
Clearly, ABCD is a quadrilateral
(ii) If the sports teacher is sitting at the origin, then which of the four students is closest to him?
(a) A
(b) B
(c) C
(d) D
 View Answer
View Answer 
Ans: (a)
Here, sports teacher is at O(0,0).
Now, 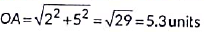
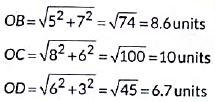
∴ OA is the minimum distance
∴ A is closest to sports teacher.
(iii) The distance between A and C is
(a) √37 units
(b) √35 units
(c) 6 units
(d) 5 units
 View Answer
View Answer 
Ans: (a)
Required distance = 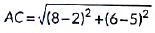
= 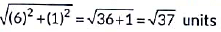
(iv) The coordinates of the mid point of line segment AC are
(a) 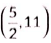
(b) 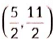
(c) 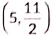
(d) (5, 11)
 View Answer
View Answer 
Ans: (c)
Coordinates of mid-point of AC are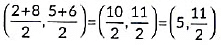
(v) If a point P divides the line segment AD in the ratio 1: 2, then coordinates of P are
(a) 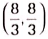
(b) 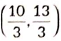
(c) 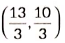
(d) 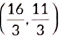
 View Answer
View Answer 
Ans: (b)
Let point P(x, y) divides the line segment AD in the ration 1: 2.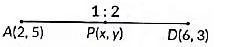
∴ 1(6) + 2(2)1 + 2 , 1(3) + 2(5)1 + 2
⇒ x = 6 + 43 , y = 3 + 103
⇒ x = 103 , y = 133
∴ Coordinates of P are ( 103 , 133 )
Previous Year Questions 2020
Q1: The distance between the points (m, -n) and (-m, n) is (2020)(a)
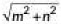
(b) m + n
(c)
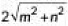
(d)
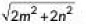
 View Answer
View Answer 
Ans: (c)
Required distance

Q2: The distance between t he points (0, 0) and (a - b, a + b) is (2020)
(a) 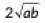
(b) 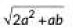
(c) 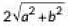
(d) 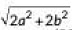
 View Answer
View Answer 
Ans: (d)
Required distance = 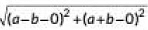
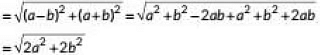
Q3: AOBC is a rectangle whose three vertices are A(0, -3), O(0, 0) and B(4, 0). The length of its diagonal is ______. (2020)
 View Answer
View Answer 
Ans: In rectangle AOBC. AB is a diagonal.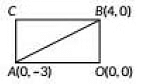
So,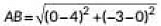
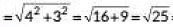
= 5 Units
Q4: Show that the points (7, 10), (-2, 5) and (3, -4) are vertices of an isosceles right triangle. (2020)
 View Answer
View Answer 
Ans: Let the given points be A(7, 10), B(-2, 5) and C(3, - 4].
Using distance Formula, we have 
Also, AB2 + BC2 = 106 + 106 = 212 = AC2
So. ABC is an isosceles right angled triangle with ∠B = 90°.
Q5: The point on the x-axis which is equidistant from (-4, 0) and (10, 0) is (2020)
(a) (7, 0)
(b) (5, 0)
(c) (0, 0)
(d) (3, 0)
 View Answer
View Answer 
Ans: (d)
To find the point on the x-axis equidistant from (-4, 0) and (10, 0), let the point be (x, 0).
Using the distance formula:
√( (x + 4)² ) = √( (x - 10)² )
Square both sides:
(x + 4)² = (x - 10)²
Expand:
x² + 8x + 16 = x² - 20x + 100
Cancel x² and simplify:
8x + 16 = -20x + 100
28x = 84
x = 3
Final Answer:
The point is (3,0).
Q6: If the point P(k, 0) divides the line segment joining the points A(2, -2) and B(-7, 4) in the ratio 1:2 then the value of k is (2020)
(a) 1
(b) 2
(c) -2
(d) -1
 View Answer
View Answer 
Ans: (d)
Since, the point P(k 0) divides the line segment joining A(2, -2) and B(-7, 4) in the ratio 1 : 2.
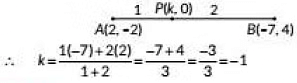
Q7: The centre of a circle whose end points of a diameter are (-6, 3) and (6, 4) is (2020)
(a) (8, -1)
(b) (4, 7)
(c) 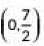
(d) 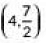
 View Answer
View Answer 
Ans: (c)
Let the coordinates of centre of the circle be (x, y) and AB be the given diameter.
By Using mid-point formula.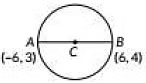
We have,
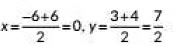
∴ Coordinates of C are 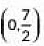
Q8: Find the ratio in which the y-axis divides the line segment joining the points (6, -4) and (-2, -7). Also, find the point of intersection. (2020)
 View Answer
View Answer 
Ans: Let the point P(0, y) on y-axis divides the line segment joining the points A(6, -4) and B(-2, -7) in the ratio k : 1.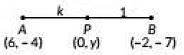
By section formula, we have
-2k + 6k + 1 = 0
⇒ -2k + 6 = 0 ⇒ k = 3
and
-7k - 4k + 1 = y
⇒ -7(3) - 43 + 1 = y
4y = -21 - 4 = -25
⇒ y = -254
Hence, the required point is (0, -254) and the required ratio is 3:1.
Q9: If the point C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3 : 4, find the coordinates of B. (2020)
 View Answer
View Answer 
Ans: We have, A(2, 5), B(x, y) and C(-1, 2) and point C divides AB in the ratio 3 :4.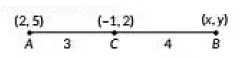
∴ -1 = 3x + 87 ⇒ -7 = 3x + 8 ⇒ x = -153 = -5
and
2 = 3y + 207 ⇒ 14 = 3y + 20 ⇒ y = -63 = -2
∴ Coordinates of B = (-5, -2)
Previous Year Questions 2019
Q1: Find the value(s) of x, if the distance between the points 4(0, 0) a nd B(x, - 4) is 5 units. (2019)
 View Answer
View Answer 
Ans: Given AB = 5 units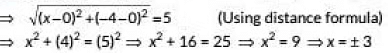
Q2: Find the point on y-axis which is equidistant from the points (5,-2) and (-3, 2). (Delhi 2019)
 View Answer
View Answer 
Ans:
Any point on the y-axis has coordinates of the form (0, y).
Set Up the Distance Equation:
The distance from (0, y) to (5, -2) should be equal to the distance from (0, y) to (-3, 2):
√((0 - 5)² + (y - (-2))²) = √((0 - (-3))² + (y - 2)²)
Simplify the equation:
√(25 + (y + 2)²) = √(9 + (y - 2)²)
Square Both Sides:
25 + (y + 2)² = 9 + (y - 2)²
Expand and Simplify:
Expand both sides:
25 + y² + 4y + 4 = 9 + y² - 4y + 4
Simplify:
29 + y² + 4y = 13 + y² - 4y
Subtract y² from both sides:
29 + 4y = 13 - 4y
Add 4y to both sides:
29 + 8y = 13
Subtract 29 from both sides:
8y = -16
Divide by 8:
y = -2
The point on the y-axis that is equidistant from (5,-2) and (-3,2) is (0,-2).
Q3: Find the coordinates of a point A where AB is a diameter of the circle with centre (-2, 2) and B is the point with coordinates (3, 4). (2019)
 View Answer
View Answer 
Ans: Let coordinates of the point A be (x, y) and O is the mid point of AB.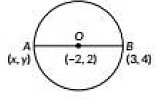
By using mid-point formula,
we have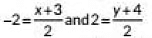
⇒ -4 = x + 3 and 4 = y + 4
⇒ x = -7 and y = 0
∴ Coordinates of A are (-7, 0).
Q4: In what ratio is the line segment joining the points P(3, -6) and Q(5, 3) divided by x-axis? (2019)
 View Answer
View Answer 
Ans: Let the point R(x, 0) on x-axis divides the line segment PQ in the ratio k: 1.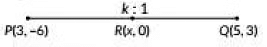
∴ By section formula, we have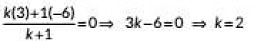
∴ Required ratio is 2 : 1 .
Q5: Find the ratio in which the segment joining the points (1, -3) and (4, 5) is divided by x-axis? Also find the coordinates of this point on x-axis. (2019)
 View Answer
View Answer 
Ans: Let the point P(x, 0) divides the segment joining the points A(1, -3) and B (4, 5) in the ratio k : 1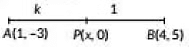
Coordinates of P are (4k + 1, 5k - 3)k + 1 (By Section Formula)
Since, y-coordinate of P is 0
5k - 3k + 1 = 0 ⇒ 5k - 3 = 0 ⇒ 5k = 3 ⇒ k = 35
Hence, the point P divides the line segment in the ratio 3:5.
Also, x-coordinate of P
= 4k + 1k + 1 = 43/5 + 1 = 178
∴ Coordinates of point P are (17/8, 0)
Q6: The point R divides the line segment AB, where A (- 4, 0) and B(0, 6) such that AR = 3/4 AB.
Find the coordinates of R. (CBSE 2019)
 View Answer
View Answer 
Ans: Given,
AR = 34 AB ⇒ ABAR = 43
⇒ ABAR - 1 = 43 - 1 = 1
⇒ AB - ARAR = 4 - 33 = 13
⇒ BRAR = 13 ⇒ AR : BR = 3:1
∴ Coordinates of R are
( 3(0) + 1(-4)3 + 1 , 3(6) + 1(0)3 + 1 )
= ( -44 , 184 ) = (-1, 92 )
Q7: Find the coordinates of point A, where AB is the diameter of the circle with centre (3, -1) and point B is (2, 6). [2019, 2 Marks]
 View Answer
View Answer 
Ans: Let the coordinates of A be (x, y). Here, 0(3, - 1] is the mid point of AB.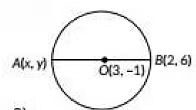
By using mid point formula, we have ⇒ x = 4, y = - 8∴ Coordinates of A are (4, - 8).
⇒ x = 4, y = - 8∴ Coordinates of A are (4, - 8).
Q8: The line segment joining the points A(2, 1) and B(5, -8) is trisected at the points P and Q such that P is nearer to A. If P also lies on the line given by 2x - y + k = 0, find the value of k. (2019)
 View Answer
View Answer 
Ans: 
Let P(x1, y1) and Q(x2, y2) are the points of trisection of line segment AB.
∴ AP = PQ = QB
Now. point P divides AB internally in the ratio 1 : 2
∴ By section formula, we have 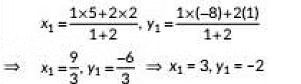
Since, point P(3, -2) lies on the line 2x - y + k = 0
⇒ 6 + 2 + k = 0
⇒ k = - 8
Q9: Find the ratio in which the line x - 3y = 0 divides the line segment joining the points (-2, -5) and (6, 3). Find the coordinates of the point of intersection. (2019)
 View Answer
View Answer 
Ans: Let point P(x1, y1) divides the line segment joining the points A(-2, -5) and B(6, 3) in the ratio k: 1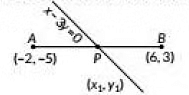
∴ Coordinates of P are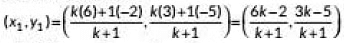
The point P lies on line x - 3y = 0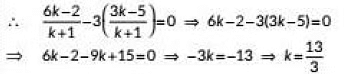
∴ Required ratio is 13 : 3.Now, coordinates of P are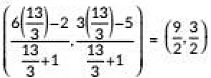
Q10: In what ratio does the point P(-4, y) divide the line segment joining the points A(-6, 10) and B(3, -8) Hence find the value of y. (2019)
 View Answer
View Answer 
Ans: Let the point P(-4, y) divides the line segment joining the points A and B in the ration k: 1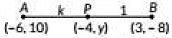
∴ By section formula, coordinates of P are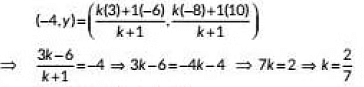
∴ Required ratio is 2: 7.
Now,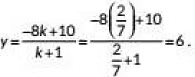
Previous Year Questions 2017
Q1: If two adjacent vertices of a parallelogram are (3, 2) and (–1, 0) and the diagonals intersect at (2, –5), then find the coordinates of the other two vertices. (CBSE 2017) View Answer
View Answer 
Ans: Consider a parallelogram ABCD with A(3, 2) and B(–1, 0).
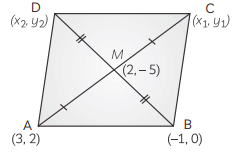
Let two adjacent vertices of a parallelogram be A ≡ (3,2) and B ≡ (-1,0).
Let coordinates of the other two vertices be C (x1, y1) and D (x2, y2).
We know that diagonals of a parallelogram bisect each other.
∴ Midpoint of AC and Midpoint of BD are the same, i.e., point O(2, -5).
∴ 3 + x12 = 2 and 2 + y12 = -5
⇒ x1 = 1 and y1 = -12 ⇒ C ≡ (1, -12)
Also, x2 - 12 = 2 and y2 + 02 = -5
⇒ x2 = 5 and y2 = -10 ⇒ D ≡ (5, -10)
Hence, the remaining vertices are (1, -12) and (5, -10).
Q2: Find the coordinates of the points of trisection of the line segment joining the points (3, –2) and (–3, –4). (CBSE 2017)
 View Answer
View Answer 
Ans: The given line segment is A(3, – 2) and B(–3, –4).
Here, C(x, y) and C'(x’, y’) are the points of trisection of AB.
Then, AC : CB = 1 : 2 and AC’ : C’B = 2 : 1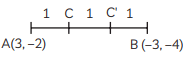
By section formula,
C(x, y) = mx2 + nx1m + n , my2 + ny1m + n
Here, m = 1, n = 2
x1 = 3, y1 = -2
x2 = -3, y2 = -4
∴ C(x, y) = 1(-3) + 2×31 + 2 , 1(-4) + 2(-2)1 + 2
= -3 + 63 , -4 - 43
= (1, -8/3)
Now,
C'(x', y') = m'x2 + n'x1m' + n' , m'y2 + n'y1m' + n'
Here, m' = 2, n' = 1
∴ C'(x', y') = 2(-3) + 1×32 + 1 , 2(-4) + 1×(-2)2 + 1
= -6 + 33 , -8 - 23
= (-1, -10/3)
Hence, the coordinates of the points of trisection are (1, -8/3) and (-1, -10/3).
Q3: In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices. (CBSE 2017)
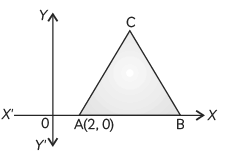
 View Answer
View Answer 
Ans: Given an equilateral triangle ABC of side 3 units.
Also, coordinates of vertex A are (2, 0).
Let the coordinates of B = (x, 0) and C = (x', y').
Then, using the distance formula,
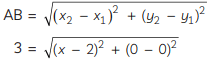
On squaring both sides, we get
9 = (x – 2)2
x2 + 4 – 4x = 9
x2 – 4x – 5 = 0
x2 – 5x + x – 5 = 0
(x – 5) (x + 1) = 0
x = 5, – 1 But x = – 1 (Neglected , since it lies on positive x-axis)
Coordinates of B are (5, 0).
Now, AC = BC [Q Sides of an equilateral triangle are equal]
or AC2 = BC2
By using the distance formula,
√(x' – 2)2 + (y' – 0)2 = √(x' – 5)2 + (y' – 0)2
x' 2 + 4 – 4x' + y' 2 = x' 2 + 25 – 10x' + y' 2
6x' = 21
x' = 7 / 2
Also, AC = 3 units. (given)
√((x - 2)² + (y' - 0)²) = 3
On squaring both sides:
x² + 4 - 4x + y'² = 9
494 + 4 - 4 × 72 + y'² = 9 [∵ x' = 72]
⇒ y'² = 9 - 94 = 274
⇒ y' = √274 = ± 3√32
But, C lies in the first quadrant.
y' = 3√32
Coordinates of C are ( 72 , 3√32 )
Hence, the coordinates of B and C are (5, 0) and ( 72 , 3√32 ) respectively.
Q4: Show that ∆ABC, where A(–2, 0), B(2, 0), C(0, 2) and ∆PQR where P(–4, 0), Q(4, 0), R(0, 4) are similar triangles. (CBSE 2017)
 View Answer
View Answer 
Ans: Given: ∆ABC with vertices A(–2, 0), B(2, 0), C(0, 2) and ∆PQR with vertices P(−4, 0) Q(4, 0) and R(0, 4).
In ∆ABC, using distance formula,
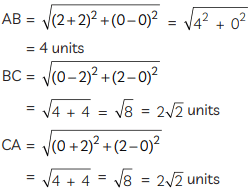
Similarly, in ∆PQR, using distance formula,
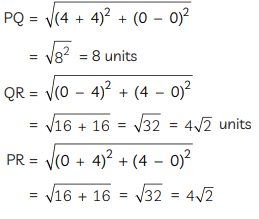
Now,
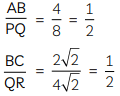
and 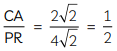
So, 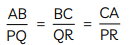
Since, the corresponding sides of ΔABC and ΔPQR are proportional,
∴ ∆ABC ~ ∆PQR
Hence, proved.
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Previous Year Questions - Coordinate Geometry
| 1. What are the key concepts of Coordinate Geometry that Class 10 students should focus on for their exams? |  |
| 2. How can students effectively prepare for Coordinate Geometry questions in their Class 10 exams? |  |
| 3. What are the common types of Coordinate Geometry questions asked in Class 10 exams? |  |
| 4. Are there any tips for solving Coordinate Geometry problems quickly during exams? |  |
| 5. How important is the understanding of Coordinate Geometry for higher studies in mathematics? |  |






















