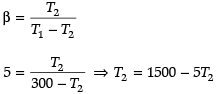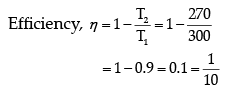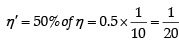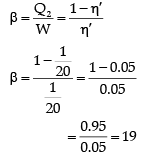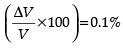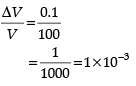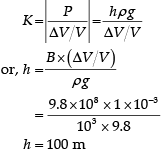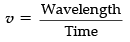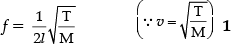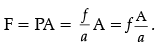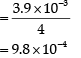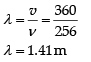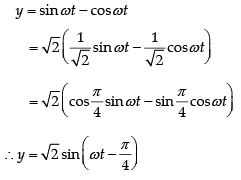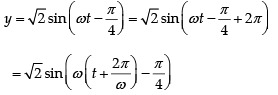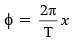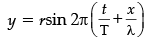Class 11 Physics: CBSE Sample Question Papers- Term II (2021-22)- 2 | Sample Papers for Class 11 Medical and Non-Medical - JEE PDF Download
| Table of contents |

|
| Class : XI |

|
| Time : 120 Minutes |

|
| Maximum Marks : 35 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class : XI
Time : 120 Minutes
Maximum Marks : 35
General Instructions:
- There are 12 questions in all. All questions are compulsory.
- This question paper has three sections: Section A, Section B and Section C.
- Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
- There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the choices in such questions.
- You may use log tables if necessary but use of calculator is not allowed..
Section - A
Q.1. Distinguish clearly between temperature and heat.
The degree of hotness of a body is called temperature. All bodies in thermal contact with each other ultimately attain the same temperature. The flow of heat energy from one body to another due to temperature difference between the two is called heat. Two bodies in thermal equilibrium with each other may not have the same amount of heat, but they must have the same temperature.
Q.2. Why the does the temperature of a gas decrease, when it is allowed to expand adiabatically?
For an adiabatic change, the first law of thermodynamics may be expressed as
dU + PdV = 0
or PdV = – dU ...(i)
During expansion, dVis + ve. Therefore the equation (i) will hold, if dU is – ve, i.e., temperature decreases.
OR
State second law of thermodynamics.
Kelvin’s statement: No process is possible whose sole result is the absorption of heat from a reservoir and complete conversion of the heat into work
Clausius statement: It is not possible to transfer heat from a body at lower temperature to another at higher temperature without the help of some external energy.
Q.3. By applying the first law of thermodynamics to isobaric process, obtain relation between two specific heats of a gas.
In an isobaric process, pressure remains constant. If an amount of heat dQ is supplied to one mole of a gas at constant pressure and its temperature increases by dT, then
dQ = CPdT
Here CP is molar specific heat of the gas at constant pressure. Therefore, for an isobaric process, the first law of thermodynamics becomes :
CPdt = dU + PdV ...(i)From perfect gas equation it follows that
PdV = RdT
In the eqn. (i), substituting PdV and dU, we have
CPdT = CVdT + RdTCP = CV + R.
Section - B
Q.4. If the coefficient performance of a refrigerator is 5 and operates at the room temperature (27°C), find the temperature inside the refrigerator.
Given: β = 5, T1 = 27ºC = 27º + 273 = 300 K
Coefficient performance of refrigerator,
T2 + 5T2 = 1500
6T2 = 1500
T2 = 1500/6 = 250 K
T2 = 250 - 273
T2 = -23ºC
Q.5. In a refrigerator one removes heat from a lower temperature and deposits to the surroundings at a higher temperature. In this process, mechanical work has to be done, which is provided by an electric motor. If the motor is of 1 kW power, and heat is transferred from −3°C to 27°C, find the heat taken out of the refrigerator per second assuming its efficiency is 50% of a perfect engine.
Given:
T1 = 27°C = 27 + 273 = 300 K
T2 = −3°C = −3 + 273 = 270 K
Efficiency of refrigerator is 50% of perfect engine.
∴ Coefficient of performance,
Q2 = 19% of work done by motor on refrigerator
=19 × 1 kW
Q2 = 19 k J/s
Q.6. To what depth must a rubber ball be taken in deep sea so that its volume is decreased by 0.1%. (The bulk modulus of rubber is 9.8 × 108 Nm−2, and the density of sea water is 103 kgm−3.)
Bulk Modulus, B = 9.8 × 108N/m2
Density of sea water (ρ) = 103kg/m3
Volume decrease (Percentage),
Let rubber ball be taken up to depth h
∴ change in pressure, P = hρg
Bulk Modulus,
Q.7. Discuss strings stretched between fixed points.
Let a spring be stretched between two points as shown in figure. Vibrations will set up in this string when it is disturbed, say from middle. The figure given below shows that vibration set up in this string appears to be similar to a half wave having wavelength λ/2.
Length of the spring l = λ/2
or λ = 2l ......(i)
If T is tension in the string and m is mass per unit length of the string, then velocity of disturbance is given by...(ii)
also
= Wavelength × Frequency
= λf
or
v = 2l × f using equ (i)
or f = v/2l ...(iii)
From equation (ii) and (iii)
Q.8. State Pascal’s law of transmission of fluid pressure. Explain how is Pascal’s law applied in a hydraulic lift. (with suitable diagram).
Pascal law: If gravity effect is neglected the pressure at every point of liquid in equilibrium at rest is same.
Hydraulic lift: It is used to lift the heavy loads. Its working is based on Pascal’s law. A simple hydraulic lift is shown in Figure. Here C and D are two cylinders of different areas of cross section. They are connected to each other with a pipe E. Each cylinder is provided with airtight frictionless piston. Let a, and A be the areas of cross-sections of the pistons in C and D respectively, where a < < A. The cylinders are filled with an incompressible liquid.Let a downward force f be applied on the piston of C. Then the pressure exerted on the liquid, P = f/a.
According to Pascal’s law, this pressure is transmitted equally to piston of cylinder D.
∴ Upward force acting on the piston of cylinder D will be
OR
A razor blade can be made to float on water. What forces act on this blade ?
When a razor blade is made to float on water, three forces act on the blade :
(i) Weight of the blade acting vertically downwards.
(ii) Reaction on blade exerted by the liquid surface acting vertically upwards.
(iii) Force of the surface tension on circumference of the blade acting tangentially to the liquid surface.
Q.9. The pattern of standing waves formed on a stretched string at two instants of time are shown in Fig. The velocity of two waves superimposing to form stationary waves is 360 ms-1 and their frequencies are 256 Hz.
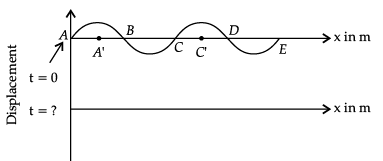 (i) Calculate the time at which the second curve is plotted.
(i) Calculate the time at which the second curve is plotted.
(ii) Mark nodes and anti-nodes on the curve.
(iii) Calculate the distance between A’ and C’.
Given: frequency of wave, ν = 256 Hz
Time period,
T = 1/v = 1/256
= 3.9 x 10-3 s
(i) Time taken to pass through mean position
t = T/4
(ii) Nodes- A, B, C, D, E ( zero displacement)
Anti-nodes-A’, C’ (maximum displacement)
(iii) At A’, C’, there are consecutive anti-nodes, so distance between A’ and C’,
Q.10. Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω
∴ (sin ωt-cos ωt) represents S.H.M.
∴ Timeperiod = 2π/ω
Q.11. What is standing wave ? Give its characteristics.
Standing or stationary wave results when two progressive waves of same wavelength and amplitude travelling with same speed in opposite directions superimpose.
Characteristics :
- Energy is not transferred from particle to particle.
- Amplitude of vibration of particles is maximum at antinode and minimum (say zero) at nodes.
- Time period of all particles is same except at nodes.
- Wavelength and frequency of standing wave is same as that of the component wave.
- Pressure variation is minimum at antinode and maximum at nodes.
OR
Obtain an equation of a progressive wave.
For a simple harmonic motion, displacement y = r sin (ωt + ϕ)
where r is amplitude, ω is angular velocity and ϕ is phase differenceBut ω = 2π/T = 2πf
andwhere λ is wavelength and x is path difference.
∴
Section - C
Q.12. Case Study : Molecular Perspective
In water, there are two types of molecules. Some molecules are at the surface, called exterior molecules, and some molecules are inside, called interior molecules. The interior molecules are attracted to all the molecules around them. The exterior molecules are attracted to only the other surface molecules and to those below the surface.
So that the energy state of the molecules on the interior is much lower than that of the molecules on the exterior. The molecules always try to maintain a lower energy state and hence the exterior molecules experience a downward force. This force is known as cohesive force. As a result they try to maintain a minimum surface area, thus allowing more molecules to have a lower energy state. Thus surface tension is created.
The water molecules attract one another due to the water molecule’s polar property. The hydrogen ends, which are positive in comparison to the negative ends of the oxygen cause water to “stick “ together. This is why there is surface tension.
Water has very high surface tension. It is 72.8 milli newton per meter at 20°C.
(i) The energy state of the interior molecules of a fluid is
(a) Higher than the exterior molecules of the fluid
(b) Lower than the exterior molecules of the fluid
(c) Equal to the exterior molecules of the fluid
(d) Higher than or Equal to the exterior molecules of the fluid
Correct Options is (b).
In water, there are two types of molecules. Some molecules are at the surface, called exterior molecules, and some molecules are inside, called interior molecules. The interior molecules are attracted to all the molecules around them. The exterior molecules are attracted to only the other surface molecules and to those below the surface. So that the energy state of the molecules on the interior is much lower than that of the molecules on the exterior.
(ii) The tendency of water to maintain .............. surface area is known as surface tension.
(a) Maximum
(b) Minimum
(c) Fixed
(d) Energetic
Correct Option is (b).
The energy state of the molecules on the interior is much lower than that of the molecules on the exterior. The molecules always try to maintain a lower energy state. As a result, they try to maintain a minimum surface area, thus allowing more molecules to have a lower energy state. Thus, surface tension is created.
(iii) The water molecules attract one another due to the water molecule’s
(a) Polar covalent bond
(b) Non-polar covalent bond
(c) Ionic bond
(d) Metallic bond
Correct Option is (a).
The water molecules attract one another due to the water molecule’s polar property. The hydrogen ends, which are positive in comparison to the negative ends of the oxygen cause water to “stick” together.
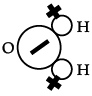
(iv) Which one of the following is the correct molecular structure of water molecule?
(a)
(b)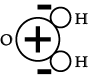
(c)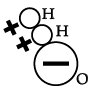
(d)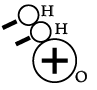
Correct Option is (a).
Water is a polar molecule having positively charged sides where the two hydrogen atoms are found and a negatively charged end where the oxygen atom is located.
(v) Surface tension of water is
(a) 72.8 mili N
(b) 72.8 N/ m
(c) 72.8 mili N /m
(d) 72.8 mili N /m2
Correct Option is (c).
Water has very high surface tension. It is 72.8 milli newton per metre at 20°C.
FAQs on Class 11 Physics: CBSE Sample Question Papers- Term II (2021-22)- 2 - Sample Papers for Class 11 Medical and Non-Medical - JEE
| 1. What is the duration of the Class XI Physics exam? |  |
| 2. What is the maximum marks for the Class XI Physics exam? |  |
| 3. How many sections are there in the Class XI Physics exam? |  |
| 4. Are the sample question papers provided by CBSE for Term II of Class XI Physics? |  |
| 5. What is the language used in the article title and exam for Class XI Physics? |  |