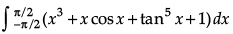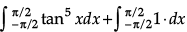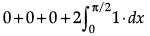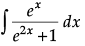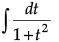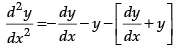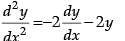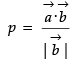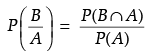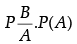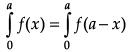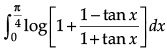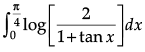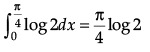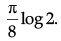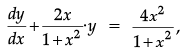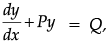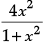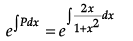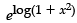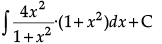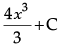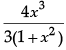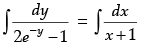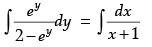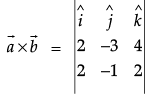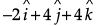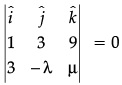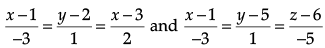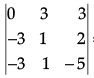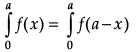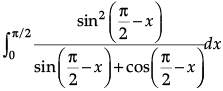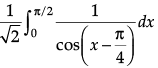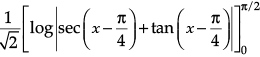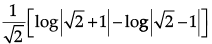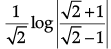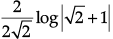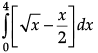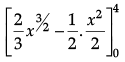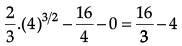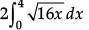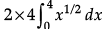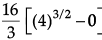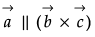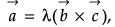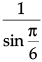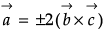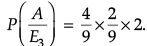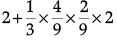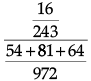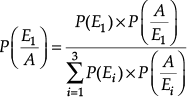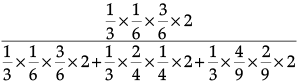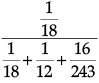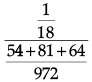Class 12 Mathematics: CBSE Sample Question Paper- Term II (2021-22)- 5 | Sample Papers for Class 12 Medical and Non-Medical PDF Download
| Table of contents |

|
| Class-XII |

|
| Time: 120 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-XII
Time: 120 Minutes
Max. Marks: 40
General Instructions :
- This question paper contains three sections A, B and C. Each part is compulsory.
- Section - A has 6 short answer type (SA1) questions of 2 marks each.
- Section - B has 4 short answer type (SA2) questions of 3 marks each.
- Section - C has 4 long answer type questions (LA) of 4 marks each.
- There is an internal choice in some of the questions.
- Q.14 is a case-based problem having 2 sub parts of 2 marks each.
Section - A
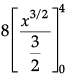
Q.1. Find the value of 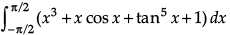
OR
Evaluate : 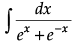
Let I =
=+
When f(x) is an even function, then,
and if f(x) is an odd function, then= 0
∴ I == π
OR
Let,
I =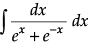
=
Also, put ex = t, ⇒ exdx = dt
⇒ I =
= tan-1t + C
= tan-1(ex) + C
Q.2. Show that 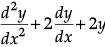 = 0 is the solution of y= e–x (A cos x + B sin x).
= 0 is the solution of y= e–x (A cos x + B sin x).
Given that, y = e–x (A cos x + B sin x)
On differentiating both sides w.r.t., x we get
dy/dx = -e-x(A cos x + B sin x) + e–x (-A sin x + B cos x)
dy/dx = -y + e-x(-A sin x + B cos x)
Again, differentiating both sides w.r.t. x, we get(-A sin x + B cos x)
⇒
⇒
⇒
⇒= 0
(Hence Proved 1)
Q.3. Find the projection of vector 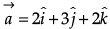 on the vector
on the vector 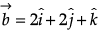 .
.
= 4 + 6 + 2 = 12
or p =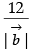
= 3
= 12/3 = 4
Q.4. If the lines 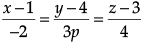 and
and 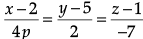 are perpendicular to each other, then find the value of p.
are perpendicular to each other, then find the value of p.
Using formula for perpendicular condition,
l1l2 + m1m2 + n1n2 = 0
or – 8p + 6p – 28 = 0
or – 2p = 28
∴ p = 14
Q.5. If P(A) = 0.4, P(B) = 0.8 and P(B/A) = 0.6, then P(A ∪ B).
Here,
P(A) = 0.4, P(B) = 0.8 and P(B/A) = 0.6
∵
⇒ P(B ∩ A) =
= 0.6 x 0.4 = 0.24
∵ P(A ∪ B) = P(A) + P(B) - P(B ∩ A)
= 0.4 + 0.8 - 0.24
= 1.2 - 0.24
= 0.96
Q.6. Find the probability distribution of X, the number of heads is a simultaneous toss of two coins.
Let X be the number of heads
Possible values of X are 0, 1, 2.
P(x = 0) = 1/4, P(x = 1) = 1/2, P(x = 2) = 1/4
The probability distribution of X is :
Section - B
Q.7.Evaluate: 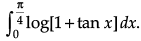
I =
..(i)
Apply the property
I =
or I =
or I =..(ii)
Adding eqn. (i) and (ii), we get
or 2I =
So, I =
Q.8. Solve 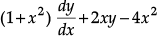 = 0 subject to the initial condition y(0) = 0.
= 0 subject to the initial condition y(0) = 0.
OR
Find the particular solution of the following differential equation :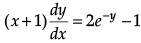 ; y = 0 when x = 0
; y = 0 when x = 0
Given differential equation can be written as:
Comparing with
⇒ P =, Q =
I.F. (Integrating factor)
=
=
= 1 + x2
∴ General solution is :
y(1 + x2) =
or, y(1 + x2) =
Putting x = 0 and y = 0, we get C = 0
∴ Solution is:
y =
OR
Given equation can be written as
⇒
⇒ -log|2 - ey| + logc = log|x + 1|
⇒ (2 - ey)(x + 1) = c
When x= 0 , y = 0 ⇒ c = 1
∴ The required solution is (2 - ey) ( x +1) = 1
Q.9. Find the area of the parallelogram whose diagonals are represented by the vectors 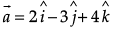 and
and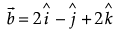 .
.
OR
Find λ and μ if 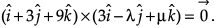
The vector equation for diagonals are
and
Now,
== √4 + 16 + 16 = √36 = 6
Area of the parallelogram
== 3 sq. units
OR= 0
or
or= 0
or 3μ + 9λ = 0 ...(i)
or μ – 27 = 0 ...(ii)
or – λ – 9 = 0 ...(iii)
From eqn. (ii) and (iii),
μ = 27
and λ = 9
Q.10. Find the value of λ, so that the lines 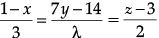 and
and 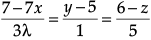
are at right angles. Also, find whether the lines are intersecting or not.
Given lines are :
and
As lines are perpendicular,= 0
⇒ λ =7
So, lines are
Consider
Δ =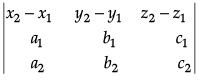
=
= -63
Since, as ∆ ≠ 0 ⇒ lines are not intersecting.
Section - C
Q.11. Show that: 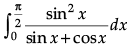 =
= 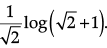
I =
...(i)
By applying property
I =
I =...(ii)
Adding eqn. (i) & (ii)
∴ 2I =
=
⇒ 2I =
=
=
I =
I =
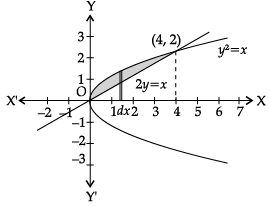
Q.12. Find the area of the region bounded by the parabola y2 = x and the line 2y = x.
OR
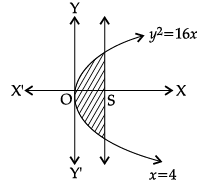
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4.
When y2 =x and 2y = x
Solving we get y2 =2y
⇒ y = 0, 2 and when y = 2, x = 4 and y = 0
⇒ x = 0
So, points of intersection are (0, 0) and (4, 2).
Graphs of parabola y2 = x and 2y = x are as shown in the adjoining figure :
From the figure, area of the shaded region,
A =
=
=
= 4/3 sq. units
Parabola y2 = 16x and line x = 4
at x = 4, y2 = 64 ⇒ y = ±8
Hence, the point of intersection (4, 8) and (4, –8)
OR
Area =
=
==
= 16/3 x 8
= 128/3 sq. units
Q.13. If  are unit vectors such that
are unit vectors such that  and the angle between
and the angle between 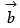 and
and
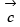 is π/6, then prove that:
is π/6, then prove that: 
As given,
both
and
are unit vectors
or
Let,
then
or= |λ|
or |λ| =
= 2
∴ λ = ±2
∴
Case-Based/Data Based
Q.14. Bag I contains 1 white, 2 black and 3 red balls; Bag II contains 2 white, 1 black and 1 red balls; Bag III contains 4 white, 3 black and 2 red balls. A bag is chosen at random and two balls are drawn from it with replacement. They happen to be one white and one red.
Based on the above information, answer the following questions:
(i) What is the probability that they came from Bag III?
(ii) What is the probability that they will come from Bag I?
Let E1 = Bag I is chosen, E2 = Bag II is chosen, E3 = Bag III is chosen, A = The two balls drawn from the chosen bag are one white and one red.
P(E1) = 1/3
= P(E2) = P(E3),,
(i) By Bayes’ Theorem, Required probability
=
=x
=
=
= 64/199
(ii) By Bayes' theorem Required probability
=
=
=
=
= 54/199
|
159 docs|4 tests
|