Class 9 Maths Chapter 4 Question Answers - Linear Equations in Two Variables
Q1: Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k.
Ans: The given equation is: 2x + 3y = k
According to the question, x = 2 and y = 1.
Now, Substituting the values of x and y in the equation 2x + 3y = k,
We get,
⇒ (2 x 2)+ (3 × 1) = k
⇒ 4+3 = k
⇒ 7 = k
⇒ k = 7
The value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k, is 7.
Q2: Write two solutions for each of the following equations:
(i) 2x + y = 7
Sol: To find the four solutions of 2x + y = 7 we substitute different values for x and y
1. Let x = 0
Then, 2x + y = 7
(2×0)+y = 7
y = 7
Therefore, one solution is = (0,7)
2. Let y = 1
Then, 2x + y = 7
2x+ 1 = 7
2x = 7 – 1
2x = 6
x = 3
Therefore, one solution is = (3, 1)
(ii) πx + y = 9
Sol: To find the four solutions of πx + y = 9 we substitute different values for x and y
1. Let x = 0
Then, πx + y = 9
(π × 0)+y = 9
y = 9
Therefore, one solution is = (0,9)
2. Let y = 0
Then, πx + y = 9
πx +0 = 9
πx = 9
x =9/π
Therefore, one solution is = (9/π,0)
Q3: The price of a notebook is twice the cost of a pen. Note a linear equation in two variables to illustrate this statement.
(Taking the price of a notebook to be ₹ x and that of a pen to be ₹ y)
Sol: Let the price of one notebook be = ₹ x
Let the price of one pen be = ₹ y
As per the question,
The price of one notebook is twice the cost of one pen.
i.e., the price of one notebook = 2×price of a pen
x = 2×y
x = 2y
x-2y = 0
x-2y = 0 is the required linear equation in two variables to illustrate the statement, ‘The price of one given notebook is twice the cost of a pen.
Q4: Find out the value of k, if x = 2, y = 1 is a given solution of the equation 2x + 3y = k.
Sol: The provided equation is
2x + 3y = k
As per the given question, x = 2 and y = 1.
Then, Replacing the values of x and y in the equation 2x + 3y = k,
We get,
⇒ (2 x 2)+ (3 × 1) = k
⇒ 4+3 = k
⇒ 7 = k
⇒ k = 7
The required value of k, if x = 2, y = 1 is a given solution of the equation 2x + 3y = k, is 7.
Q5: Establish that the required points A (1, 2), B ( – 1, – 16) and C (0, – 7) lie on the graph of the required linear equation y = 9x – 7.
Sol: We include the equation,
y = 9x – 7
For A (1, 2),
Replacing (x,y) = (1, 2),
We obtain,
2 = 9(1) – 7
2 = 9 – 7
2 = 2
For B (–1, –16),
Replacing (x,y) = (–1, –16),
We get,
–16 = 9(–1) – 7
-16 = – 9 – 7
-16 = – 16
For C (0, –7),
Replacing (x, y) = (0, –7),
We obtain,
– 7 = 9(0) – 7
-7 = 0 – 7
-7 = – 7
Therefore, the points A (1, 2), B (–1, –16) and C (0, –7) satisfy the line y = 9x – 7.
Therefore, A (1, 2), B (–1, –16) and C (0, –7) are answers to the linear equation y = 9x – 7
Thus, points A (1, 2), B (–1, –16), and C (0, –7) lie on the graph of the linear equation y = 9x – 7.
Q6: Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) x – y/5 – 10 = 0
(ii) -2x + 3y = 6
(iii) y – 2 = 0
Sol:
(i) The equation x - y/5 - 10 = 0 can be written as:
(1)x + (-1/5) y + (-10) = 0
Now compare the above equation with ax + by + c = 0
Thus, we get;
a = 1
b = -1/5
c = -10
(ii) –2x + 3y = 6
Re-arranging the given equation, we get,
–2x + 3y – 6 = 0
The equation –2x + 3y – 6 = 0 can be written as,
(–2)x + 3y +(– 6) = 0
Now comparing (–2)x + 3y +(– 6) = 0 with ax + by + c = 0
We get, a = –2
b = 3
c = -6
(iii) y – 2 = 0
y – 2 = 0
The equation y – 2 = 0 can be written as,
0x + 1y + (–2) = 0
Now comparing 0x + 1y + (–2) = 0with ax + by + c = 0
We get, a = 0
b = 1
c = –2
Q7: Give the geometric representations of 2x + 9 = 0 as an equation
(i) in one variable
(ii) in two variables
Sol:
(i) 2x + 9 = 0
We have, 2x + 9 = 0
2x = – 9
x = -9/2
which is the required linear equation in one variable, that is, x only.
Therefore, x= -9/2 is a unique solution on the number line as shown below:
(ii) 2x +9=0
We can write 2x + 9 = 0 in the two variables as 2x + 0, y + 9 = 0
or x = −9−0.y/2
∴ When y = 1, x = −9−0.(1)/2 = -9/2
y=2 , x = −9−0.(2)/2 = -9/2
y = 3, x = −9−0.(3)/2= -9/2
Therefore, we obtain the following table: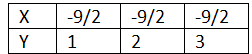
Now, plotting the ordered pairs (−9/2,3), (−9/2,3) and (−9/2,3) on graph paper and connecting them, we get a line PQ as the solution of 2x + 9 = 0.
Q8: Find the value of k for which x = 0, y = 8 is a solution of 3x – 6y = k.
Sol: Since x = 0 and y = 8 is a solution of given equation
3x – 6y = k
3(0) – 6(8) = k
⇒ k = – 48
Q9: The cost of a table is 100 more than half the cost of a chair. Write this statement as a linear equation in two variables.
Sol: Let the cost price of a table be ₹ x and that of a chair be ₹ y.
Since the cost price of a table is 100 more than half the cost price of a chair.
∴ x = 1/2y + 100
⇒ 2x = y + 200 or 2x – y – 200 = 0.
Q10: Give equation of two lines on same plane which are intersecting at the point (2, 3).
Sol: Since there are infinite lines passing through the point (2, 3).
Let, first equation is x + y = 5 and second equation is 2x + 3y = 13.
Clearly, the lines represented by both equations intersect at the point (2, 3).
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Chapter 4 Question Answers - Linear Equations in Two Variables
| 1. What are linear equations in two variables? |  |
| 2. How can we graph a linear equation in two variables? |  |
| 3. What is the significance of the solutions of a linear equation in two variables? |  |
| 4. How can we determine if two linear equations in two variables are parallel? |  |
| 5. What methods can be used to solve a system of linear equations in two variables? |  |






















