Class 9 Maths Chapter 4 Question Answers - Linear Equations in Two Variables
Question 1. Is (3, 2) a solution of x + y = 6?
Solution: (3, 2) means x = 3 and y = 2
∴ Substituting x = 3 and y = 2 in x + y = 6,
we have 3 + 2 = 6
⇒ 5 = 6 which is not correct Since
L.H.S. ≠ R.H.S.
∴ (3, 2) is not a solution of x + y = 6.
Question 2. Is  a solution of 2x + 3y = 12?
a solution of 2x + 3y = 12?
Solution: The given equation is 2x + 3y = 12 ...(1)
Here Solution = 
⇒ x = 2 and y = (8/3)
Substituting x = 2 and y =(8/3) in (1), we get

⇒ 4 + 8 = 12
⇒ 12 = 12
∵ L.H.S. = R.H.S
∴ is a solution of 2x + 3y = 12.
is a solution of 2x + 3y = 12.
Question 3. Express 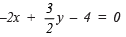 in the form of ax + by + c = 0 and write the value of a, b and c.
in the form of ax + by + c = 0 and write the value of a, b and c.
Solution: We have 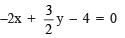
⇒ 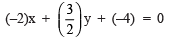 ...(1)
...(1)
Comparing (1) with ax + by + c = 0, we have
a = –2, b = (3/2) and c = –4.
Question 4. Express 2x = 5 in the form ax + by + c = 0 and find the value of a, b and c.
Solution: 2x = 5 can be written as 2x – 5 = 0
⇒ 2x + (0)y – 5 = 0
⇒ 2x + (0)y + (–5) = 0 ...(1)
Comparing (1) with ax + by + c = 0, we get
a = 2, b = 0 and c = –5.
Question 5. Write two solutions of 3x + y = 8.
Solution: We have 3x + y = 8
For x = 0, we have 3(0) + y = 8
⇒ 0 x y= 8 ⇒ y = 8
 .e. (0, 8) is a solution.
.e. (0, 8) is a solution.
For x = 1, we have 3(1) + y = 8
⇒ 3 + y = 8
⇒ y = 8 – 3 = 5
 i.e. (1, 5) is another solution.
i.e. (1, 5) is another solution.
Question 6. If x = –1 and y = 2 is a solution of kx + 3y = 7, find the value k.
Solution: We have kx + 3y = 7 ...(1)
∴ Putting x = –1 and y = 2 in (1), we get
k(–1) + 3(2) = 7
⇒ –k + 6 = 7
⇒ –k = 7 – 6 = 1
⇒ k= –1
Thus, the required value of k = –1.
Question 7. Show that x = 2 and y = 1 satisfy the linear equation 2x + 3y = 7.
Solution: We have 2x + 3y = 7 ...(1)
Since, x = 2 and y = 1 satisfy the equation (1).
∴ Substituting x = 2 and y = 1 in (1), we get
L.H.S. = 2(2) + 3(1) = 4 + 3 = 7
= R.H.S.
Since, L.H.S. = R.H.S.
∴ x = 2 and y = 1 satisfy the given equation.
Question 8. Write four solutions of 2x + 3y = 8.
Solution: We have 2x + 3y = 8 ...(1)
Let us assume x = 0.
∴ Substituting x = 0 in (1), we get
2(0) + 3y = 8
⇒ 0 + 3y = 8
⇒ y= (8/3)
∴  is a solution of (1)
is a solution of (1)
Again assume y = 0.
∴ From (1), we have
2x + 3(0) = 8
⇒ 2x = 8
⇒ x= (8/2) = 4
∴ (4, 0) is a solution of (1).
Again assume x = 1.
∴ From (1), we have
2(1) + 3y = 8
⇒ 3y = 8 – 2 = 6
⇒ y = (6/3) = 2
∴ (1, 2) is a solution of (1).
Again assume x = 2.
∴ From (1), we have
2(2) + 3y = 8
⇒ 4 + 3y = 8
⇒ 3y = 8 – 4 = 4
⇒ y = (4/3)
∴ is a solution of (1).
is a solution of (1).
∴ The required four solutions are: , (4, 0), (1, 2) and
, (4, 0), (1, 2) and
|
40 videos|420 docs|51 tests
|
FAQs on Class 9 Maths Chapter 4 Question Answers - Linear Equations in Two Variables
| 1. What are linear equations in two variables? |  |
| 2. How do you solve a linear equation in two variables? |  |
| 3. What is the graphical representation of a linear equation in two variables? |  |
| 4. Can a linear equation in two variables have infinitely many solutions? |  |
| 5. How can linear equations in two variables be used in real-life situations? |  |



























