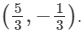Coordinate Geometry Exercise 14.1 (Part-10) | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 1: Find the centroid of the triangle whose vertices are:
(i) (1, 4) (−1,−1), (3, −2)
(ii) (−2, 3) (2, −1) (4, 0)
Answer :
We know that the co-ordinates of the centroid of a triangle whose vertices are 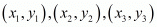 is-
is-
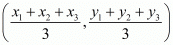
(i) The co-ordinates of the centroid of a triangle whose vertices are (1, 4); (−1,−1); (3,−2) are-
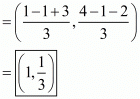
(ii) The co-ordinates of the centroid of a triangle whose vertices are (−2, 3); (2,−1); (4, 0) are-
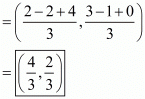
Question 2:Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
Answer :
We have to find the co-ordinates of the third vertex of the given triangle. Let the co-ordinates of the third vertex be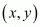 .
.
The co-ordinates of other two vertices are (1, 2) and (3, 5)
The co-ordinate of the centroid is (0, 0)
We know that the co-ordinates of the centroid of a triangle whose vertices are 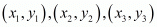 is−
is−
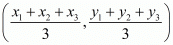
So,
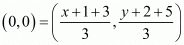
Compare individual terms on both the sides-

So,
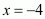
Similarly,
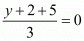
So,
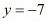
So the co-ordinate of third vertex 
Question 3: Find the third vertex of a triangle, if two of its vertices are at (−3, 1) and (0, −2) and the centroid is at the origin.
Answer :
We have to find the co-ordinates of the third vertex of the given triangle. Let the co-ordinates of the third vertex be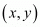 .
.
The co-ordinates of other two vertices are (−3, 1) and (0, −2)
The co-ordinate of the centroid is (0, 0)
We know that the co-ordinates of the centroid of a triangle whose vertices are 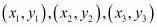 is-
is-
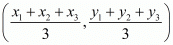
So,

Compare individual terms on both the sides-
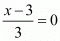
So,
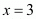
Similarly,
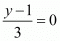
So,
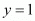
So the co-ordinate of third vertex 
Question 4: A (3, 2) and B (−2, 1) are two vertices of a triangle ABC whose centroid G has the coordinates  Find the coordinates of the third vertex C of the triangle.
Find the coordinates of the third vertex C of the triangle.
Answer :
We have to find the co-ordinates of the third vertex of the given triangle. Let the co-ordinates of the third vertex be .
.
The co-ordinates of other two vertices are A (3, 2) and C (−2, 1)
The co-ordinate of the centroid is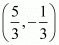
We know that the co-ordinates of the centroid of a triangle whose vertices are 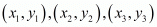 is-
is-
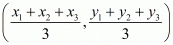
So,
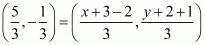
Compare individual terms on both the sides-
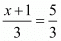
So,
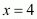
Similarly,
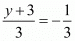
So,
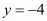
So the co-ordinate of third vertex 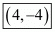
Question 5: If (−2, 3), (4, −3) and (4, 5) are the mid-points of the sides of a triangle, find the coordinates of its centroid.
Answer :
Let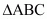 be ant triangle such that P (−2, 3); Q (4,−3) and R (4, 5) are the mid-points of the sides AB, BC, CA respectively.
be ant triangle such that P (−2, 3); Q (4,−3) and R (4, 5) are the mid-points of the sides AB, BC, CA respectively.
We have to find the co-ordinates of the centroid of the triangle.
Let the vertices of the triangle be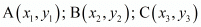
In general to find the mid-point of two points
of two points and
and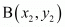 we use section formula as,
we use section formula as,
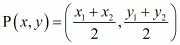
So, co-ordinates of P,
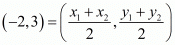
Equate the x component on both the sides to get,
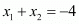 …… (1)
…… (1)
Similarly,
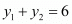 …… (2)
…… (2)
Similarly, co-ordinates of Q,
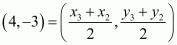
Equate the x component on both the sides to get,
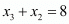 …… (3)
…… (3)
Similarly,
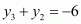 …… (4)
…… (4)
Similarly, co-ordinates of R,
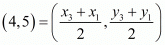
Equate the x component on both the sides to get,
 …… (5)
…… (5)
Similarly,
 …… (6)
…… (6)
Add equation (1) (3) and (5) to get,
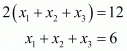
Similarly, add equation (2) (4) and (6) to get,
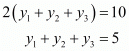
We know that the co-ordinates of the centroid G of a triangle whose vertices are  is-
is-
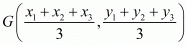
So, centroid G of a triangle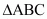 is,
is,
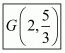
Question 6: Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
Answer :
Let be any triangle such that O is the origin and the other co-ordinates are
be any triangle such that O is the origin and the other co-ordinates are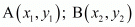 . P and R are the mid-points of the sides OA and OB respectively.
. P and R are the mid-points of the sides OA and OB respectively.
We have to prove that line joining the mid-point of any two sides of a triangle is equal to half of the third side which means,
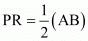
In general to find the mid-point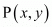 of two points
of two points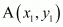 and
and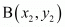 we use section formula as,
we use section formula as,
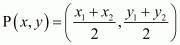
So,
Co-ordinates of P is,
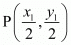
Similarly, co-ordinates of R is,
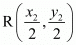
In general, the distance between A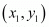 and B
and B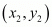 is given by,
is given by,
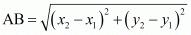
Similarly,
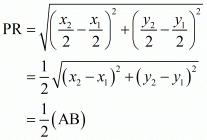
Hence,

|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|