Co­ordinate Geometry Exercise 14.1 (Part-5) | Extra Documents, Videos & Tests for Class 10 PDF Download

Question 1: Find the coordinates of the point which divides the line segment joining (−1,3) and (4, −7) internally in the ratio 3 : 4

Answer : 

We have A (−1, 3) and B (4,−7) be two points. Let a point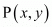divide the line segment joining the points A and B in the ratio 3:4 internally.

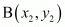Now according to the section formula if point a point P divides a line segment joining andin the ratio m: n internally than,

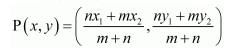
Now we will use section formula to find the co-ordinates of unknown point P as,

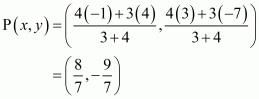
Therefore, co-ordinates of point P is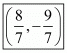

Question 2: Find the points of trisection of the line segment joining the points:
(a) 5, −6 and (−7, 5),
(b) (3, −2) and (−3, −4),
(c) (2, −2) and (−7, 4).

Answer :

The co-ordinates of a point which divided two points 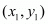 and 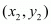 internally in the ratio 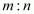is given by the formula,

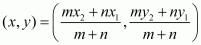
The points of trisection of a line are the points which divide the line into the ratio.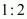

(i) Here we are asked to find the points of trisection of the line segment joining the points A(5,−6) and B(−7,5).

So we need to find the points which divide the line joining these two points in the ratio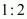 and 2 : 1.

Let P(x, y) be the point which divides the line joining ‘AB’ in the ratio 1 : 2.

Let Q(e, d) be the point which divides the line joining ‘AB’ in the ratio 2 : 1.

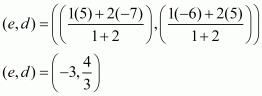
Therefore the points of trisection of the line joining the given points are .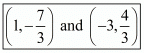

(ii) Here we are asked to find the points of trisection of the line segment joining the points A(3,−2) and B(−3,−4).

So we need to find the points which divide the line joining these two points in the ratio and 2 : 1.

Let P(x, y) be the point which divides the line joining ‘AB’ in the ratio 1 : 2.

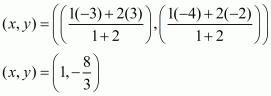
Let Q(e, d) be the point which divides the line joining ‘AB’ in the ratio 2 : 1.

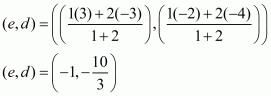
Therefore the points of trisection of the line joining the given points are.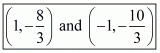

(iii) Here we are asked to find the points of trisection of the line segment joining the points A(2,−2) and B(−7,4).

So we need to find the points which divide the line joining these two points in the ratio and 2 : 1.

Let P(x, y) be the point which divides the line joining ‘AB’ in the ratio 1 : 2.

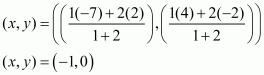
Let Q(e, d) be the point which divides the line joining ‘AB’ in the ratio 2 : 1.

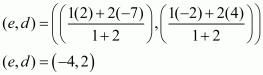
Therefore the points of trisection of the line joining the given points are .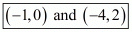

Question 3: Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (−2, −1), (1, 0), (4, 3) and(1, 2) meet.

Answer :

The co-ordinates of the midpoint 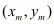 between two points  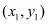and  is given by,

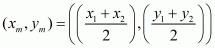
In a parallelogram the diagonals bisect each other. That is the point of intersection of the diagonals is the midpoint of either of the diagonals.

Here, it is given that the vertices of a parallelogram are A(−2,−1), B(1,0) and C(4,3) and D(1,2).

We see that ‘AC’ and ‘BD’ are the diagonals of the parallelogram.

The midpoint of either one of these diagonals will give us the point of intersection of the diagonals.

Let this point be M(x, y).

Let us find the midpoint of the diagonal ‘AC’.

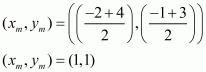
Hence the co-ordinates of the point of intersection of the diagonals of the given parallelogram are.

Question 4: Prove that the points (3, −2), (4, 0), (6, −3) and (5, −5) are the vertices of a parallelogram.

Answer :

Let A (3,−2); B (4, 0); C (6,−3) and D (5,−5) be the vertices of a quadrilateral. We have to prove that the quadrilateral ABCD is a parallelogram.

We should proceed with the fact that if the diagonals of a quadrilateral bisect each other than the quadrilateral is a parallelogram.

Now to find the mid-point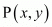 of two points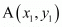and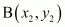 we use section formula as,

So the mid-point of the diagonal AC is,

Similarly mid-point of diagonal BD is,

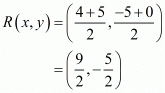
Therefore the mid-points of the diagonals are coinciding and thus diagonal bisects each other.

Hence ABCD is a parallelogram.