Concept of Solid Angle | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
CONCEPT OF SOLID ANGLE

Solid angle is a generalisation of the plane angle: In figure we show a plane curve AB. The end points A and B are joined to the point O. We say that the curve AB subtends an angle or a plane angle at O. An angle is formed at O by the two lines OA and OB passing through O. We say that the curve AB subtends an angle or a plane angle at O. An angle is formed at O by the two lines OA and OB passing through O.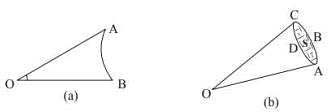 To construct a solid angle, we start with a surface S (fig.) and join all the points on the periphery such as A, B, C, D etc., with the given point O. We then say that a solid angle is formed at O and that the surface S has subtended the solid angle. The solid angle is formed by the lines joining the points on the periphery with O. The whole figure looks like a cone. As a typical example, think of the paper containers used by Mungfali Wala.
To construct a solid angle, we start with a surface S (fig.) and join all the points on the periphery such as A, B, C, D etc., with the given point O. We then say that a solid angle is formed at O and that the surface S has subtended the solid angle. The solid angle is formed by the lines joining the points on the periphery with O. The whole figure looks like a cone. As a typical example, think of the paper containers used by Mungfali Wala.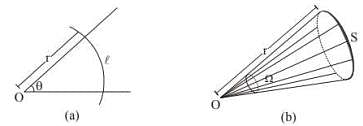 How do we measure a solid angle? Let us consider how do we measure a plane angle. See fig. We draw a circle of any radius r with the centre at O and measure the length 𝑙 of the arc intercepted by the angle.
How do we measure a solid angle? Let us consider how do we measure a plane angle. See fig. We draw a circle of any radius r with the centre at O and measure the length 𝑙 of the arc intercepted by the angle.
The angle 𝜃 is then defined as 𝜃 = 1/r. In order to measure a solid angle at the point O (fig.), we draw a sphere of any radius r with O as the centre and measure the area S of the part of the sphere intercepted by the cone. The solid angle Ω is then defined as Ω = S/r2
Note: That this definition makes the solid angle a dimensionless quantity. It is independent of the radius of the sphere drawn.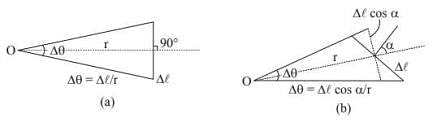 Next, consider a plane angle subtended at a point O by a small line segment Δℓ (fig.). Suppose, the line joining O to the middle point of Δℓ is perpendicular to Δℓ.As the segmentis small, we can approximately write.
Next, consider a plane angle subtended at a point O by a small line segment Δℓ (fig.). Suppose, the line joining O to the middle point of Δℓ is perpendicular to Δℓ.As the segmentis small, we can approximately write.
Δ𝜃 =Δℓ/r
As Δℓ gets smaller, the approximation becomes better. Now suppose, the line joining O to Δℓ is not perpendicular to Δℓ (fig.). Suppose, this line makes an angle 𝛼 with the perpendicular to Δℓ. The angle subtended by Δℓ at O is
Δ𝜃 = Δℓcos 𝛼/r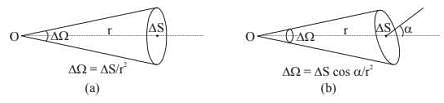 Similarly, if a small plane area ΔS (fig.) subtends a solid angle Δℓ at O in such a way that the line joining O to ΔS is normal to ΔS, we can writeΔ Ω = ΔS / r2.
Similarly, if a small plane area ΔS (fig.) subtends a solid angle Δℓ at O in such a way that the line joining O to ΔS is normal to ΔS, we can writeΔ Ω = ΔS / r2.
But if the line joining O to ΔS makes an angle 𝛼 with the normal to ΔS (fig.), we should write
ΔΩ = ΔScos 𝛼/r2
A complete circle subtends an angle
𝜃 = ℓ/r = 2𝜋r/r = 2𝜋
at the centre. In fact, any closed curve subtends an angle 2π at an y of the internal points. Similarly, a complete sphere subtends a solid angle,
Ω = S/r2 = 4𝜋𝑟2/r2 = 4𝜋
at the centre. Also, any closed surface subtends a solid angle 4π at any internal point.
How much is the angle subtended by a closed plane curve at an external point?
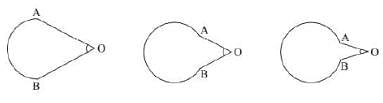 See fig. As we gradually close the curve, the angle finally diminishes to zero. A closed curve subtends zero angle at an external point. Similarly, a closed surface subtends zero solid angle at an external point.
See fig. As we gradually close the curve, the angle finally diminishes to zero. A closed curve subtends zero angle at an external point. Similarly, a closed surface subtends zero solid angle at an external point.
APPLICATION OF SOLID ANGLE
Q. Fraction of light emerging from an isotropic point source through a conical region having semi vertex angle 𝛼 and with its apex at the source.
Ans. Let us consider a sphere of radius R with its centre at the source S. Let AB be the section (circular) where the cone ASB intercepts the sphere. If ΔS be the area of the spherical portion ACB (lying within the conical region) then, the solid angle
Let AB be the section (circular) where the cone ASB intercepts the sphere. If ΔS be the area of the spherical portion ACB (lying within the conical region) then, the solid angle
Ω = ΔS/R2
Let SC be the symmetry axis of the portion of the sphere ACB.
If x be the distance of a thin circular strip then its area
dS = 2𝜋 x Rd𝜃
= 2𝜋 (Rsin 𝜃) Rd𝜃
Total Area,
ΔS = ∫ dS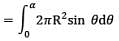
= 2𝜋R2 [1 − 𝐜𝐨s 𝜶]
Therefore, area of the curved surface ΔS which subtends an angle 𝛼 at the center,
ΔS = 2𝜋R2 [1 − 𝐜𝐨s 𝜶]
Also, Solid Angle
𝛀 = S/R2 = 2𝜋 [1 − 𝐜𝐨s 𝜶]
This relation between plane angle 𝛼 and solid angle 𝛀 is advised to be remembered.
If Ω steradian be the solid angle for the cone then, the fraction of light passing through the cone will be
|
199 videos|422 docs|281 tests
|
FAQs on Concept of Solid Angle - Physics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What is the concept of solid angle? |  |
| 2. How is solid angle different from regular angle? |  |
| 3. What is the formula to calculate solid angle? |  |
| 4. How is solid angle used in physics? |  |
| 5. Can solid angle be negative? |  |

















