Revision Notes: Electrostatic
Charge
It is the inherent property of certain fundamental particles. It accompanies them wherever they exist. Commonly known charged particles are proton and electron. The charge of a proton is taken as positive and that of electron is taken as negative. It is represented by symbol e.
e = 1.6 × 10-19 coulomb.
Positive and negative sign were arbitrarily assigned by Benzamin Franklin. This does not mean that charge of proton is greater than charge of electron.
Quantization of Charge
Electric charges appear only in discrete amounts, it is said to be quantized.
Conservation of Charge
For an isolated system, the total charge remains constant, charge is neither created nor destroyed, and it is transferred from one body to the other.
Coulomb's Law
The force of interaction of two stationary point charges in vacuum is directly proportional to the product of these charges and inversely proportional to the square of their separation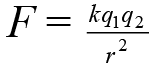
Where, k is a constant which depends on the system of units. Its value in SI unit is
k = 9 × 109 Nm2C-2
The constant is often written in the form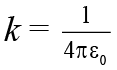
Where, ε0 is called the permittivity constant which is numerically equal to
ε0 = 8.85 × 10-12 C2 /Nm2
Electric Field
The electric field strength (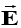
) at a point is defined as the force per unit charge experienced by a test charge qt, placed at that point.
Lines of Force
The electric field lines or lines of force are helpful in visualizing field patterns. They provide the following basic information:
(a) The direction of the field is along the tangent to a line of force.
(b) The strength or magnitude of the field is proportional to the number of lines that cross a unit area perpendicular to the line.
Gauss' Law
The net flux of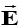 
through a closed surface equals 1/ε0 times the net charge enclosed by the surface.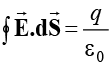
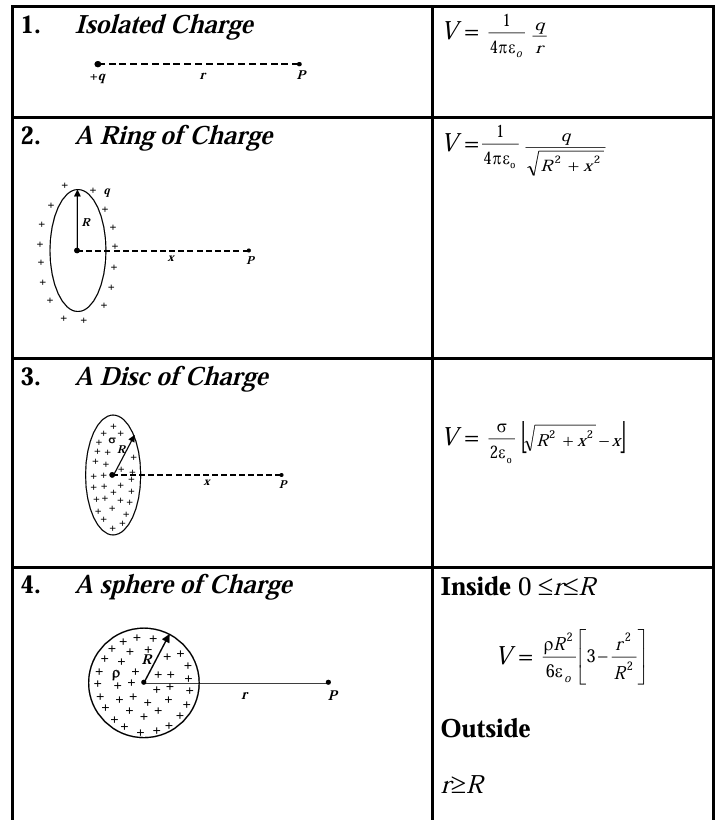
Electric field E due to Various Charge Distributions
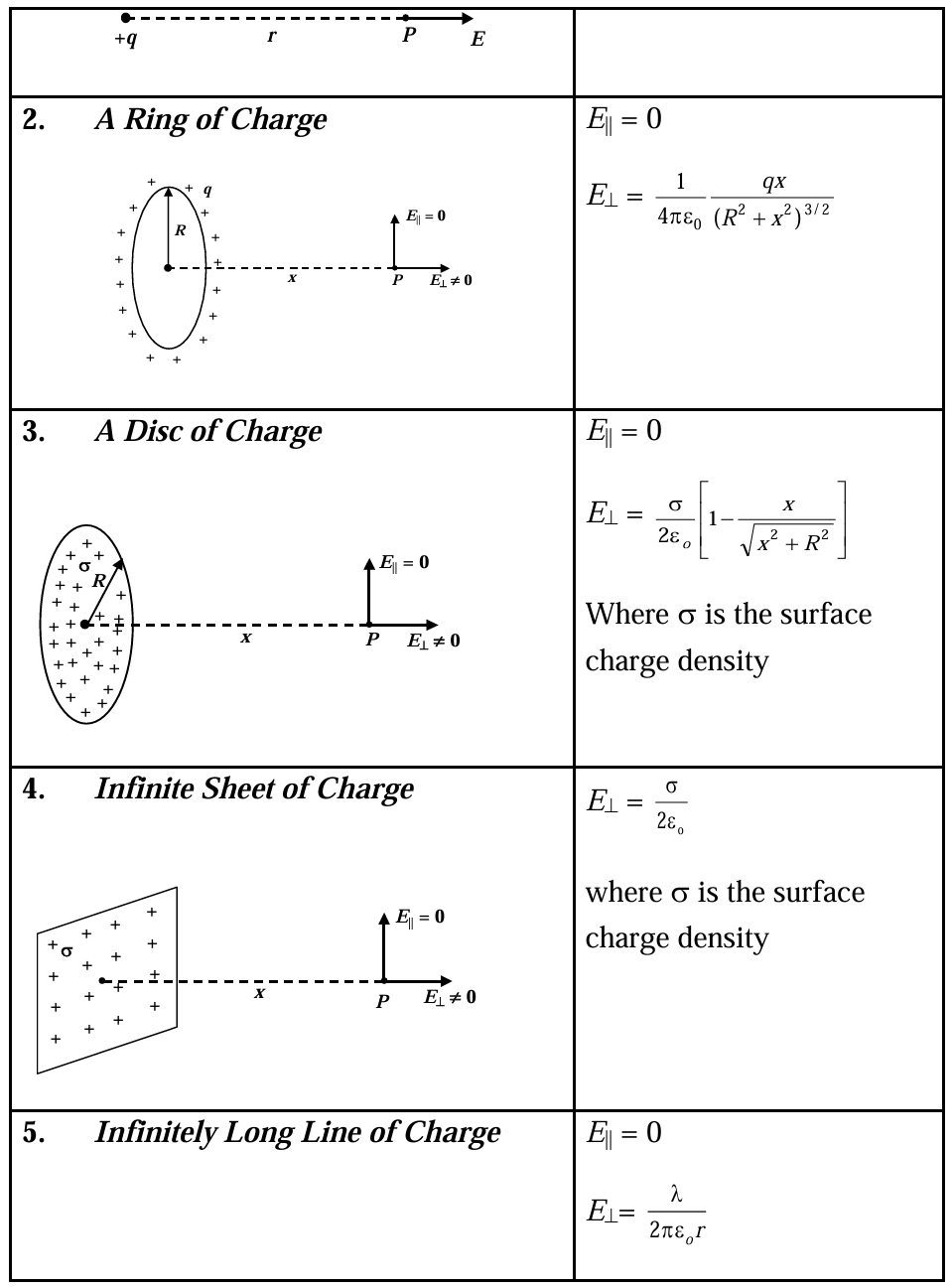
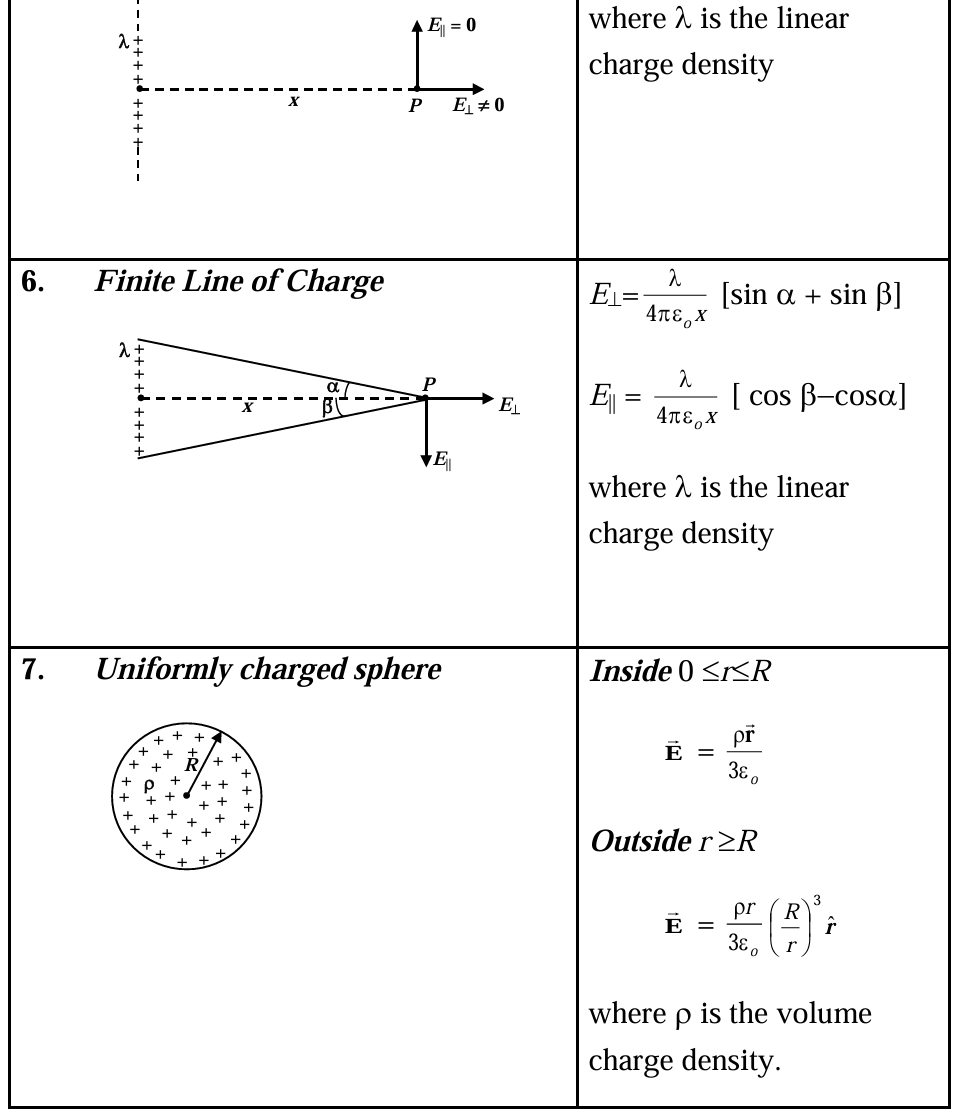
Potential
Electric potential, ΔV is defined as the change in electrostatic potential energy per unit charge.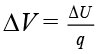
The SI unit of electric potential is the volt (V).
Relationship between E and V
We know that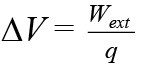
Now
Electric Potential V due to Various Charge Distribution
1. Electric field intensity due to Dipole
(i) Along the axis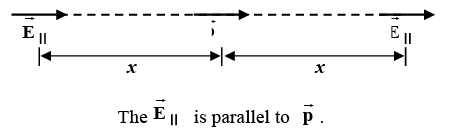
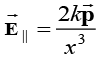The direction of electric field along the axis is in the same direction as that of the dipole moment.
(ii) Along the bisector
The direction of electric field along the bisector is opposite to that of the dipole moment.
2. Electric Potential Due to a Dipole Moment
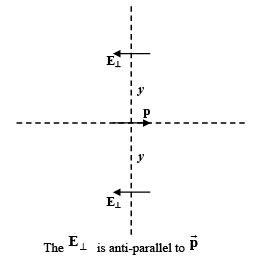(i) Along the axis
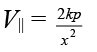(ii) Along the bisector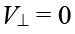
3. Dipole in an External Uniform Field
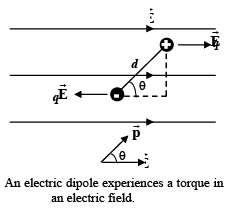(i) Torque: If a dipole is oriented at an angle θ to an uniform electric field as shown in the figure, the charges experience equal and opposite forces. So there is no net force on the dipole. However, there is a net torque on the dipole.
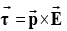The magnitude of the torque is t = p E sin θ
(ii) Potential Energy: The potential energy of a dipole in an external field is given by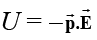
Capacitors
A capacitor is a device that stores electrical energy. The capacitance of the capacitor is defined as the magnitude of the charge on one plate divided by the magnitude of the potential difference V between them
C = q/v
Capacitance depends on the size and shape of the plates and the material between them. It does not depend on q or V individually. The SI unit of capacitance is the farad (F).
1 farad = 1 coulomb/volt
1. Parallel Plate Capacitor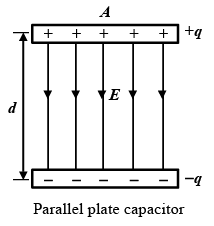
2. Spherical Capacitor
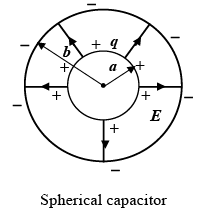
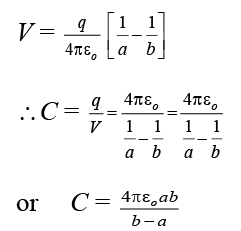
3. Cylindrical Capacitor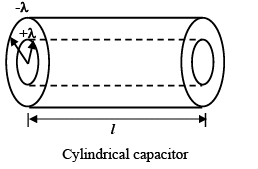
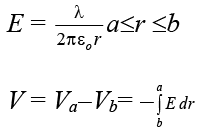
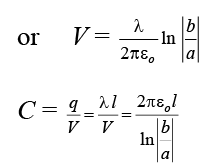
Energy stored in a Capacitor
The energy stored in a capacitor is equal to the work done to charge it.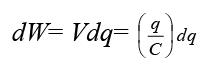 
The charge moves through the wires, not across the gap between the plates. The total work done to transfer charge Q is
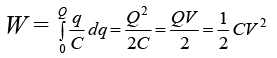Since the charge on each plate is unaffected the capacitance in the presence of the dielectric is
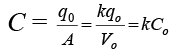The capacitance of the capacitor increases by a factor k.
FAQs on Revision Notes: Electrostatic
| 1. What is the difference between electric field and electric potential in electrostatics? |  |
| 2. How do I calculate electric flux using Gauss's law for different charge configurations? | |
| 3. Why does electric potential energy change when charges move in an electric field? | |
| 4. What are the most common mistakes students make with Coulomb's law and superposition principle? | |
| 5. How should I approach problems involving conductors and insulators in electric fields? | |
