Coordinate Geometry Exercise 14.1 (Part-12) | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 1: Find the area of a triangle whose vertices are
(i) (6, 3) (−3, 5) and (4, −2)
(ii) (at21, 2at1), (at22,2at2) and (at23,2at3)
(iii) (a, c + a), (a, c) and (−a, c − a)
Answer :
We know area of triangle formed by three points 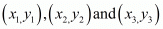 is given by
is given by
(i) The vertices are given as (6, 3), (−3, 5), (4, −2).

(ii) The vertices are given as 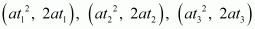 .
.
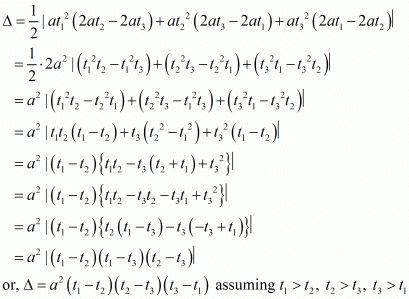
(iii) The vertices are given as 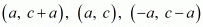 .
.
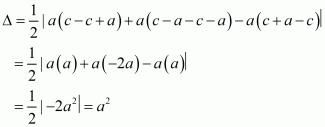
Question 2:
Find the area of the quadrilaterals, the coordinates of whose vertices are
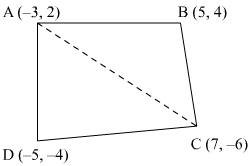
(i) (−3, 2), (5, 4), (7, −6) and (−5, −4)
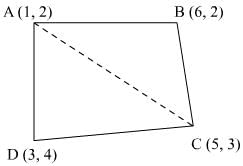
(ii) (1, 2), (6, 2), (5, 3) and (3, 4)
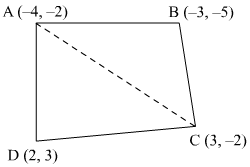
(iii) (−4, −2, (−3, −5), (3, −2), (2, 3)
Answer :
(i) Let the vertices of the quadrilateral be A (−3, 2), B (5, 4), C (7, −6), and D (−5, −4). Join AC to form two triangles ΔABC and ΔACD.
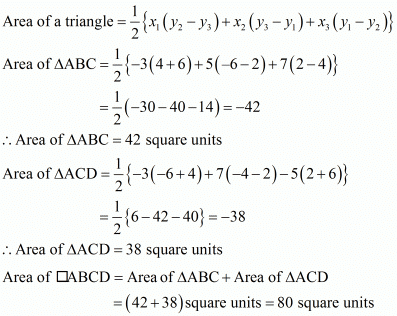
(ii) Let the vertices of the quadrilateral be A (1, 2), B (6, 2), C (5, 3), and D (3, 4). Join AC to form two triangles ΔABC and ΔACD.

(iii) Let the vertices of the quadrilateral be A (−4, −2), B (−3, −5), C (3, −2), and D (2, 3). Join AC to form two triangles ΔABC and ΔACD.
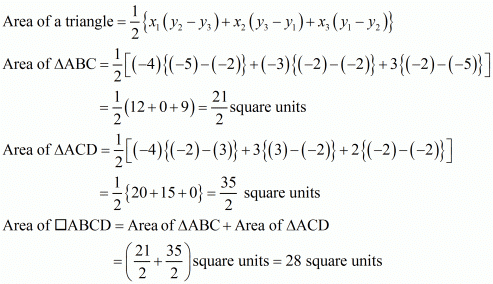
Question 3: The four vertices of a quadrilateral are (1, 2), (−5, 6), (7, −4) and (k, −2) taken in order. If the area of the quadrilateral is zero, find the value of k.
Answer :
GIVEN: The four vertices of quadrilateral are (1, 2), (−5, 6), (7, −4) and D (k, −2) taken in order. If the area of the quadrilateral is zero
TO FIND: value of k
PROOF: Let four vertices of quadrilateral are A (1, 2) and B (−5, 6) and C (7, −4) and D (k, −2)
We know area of triangle formed by three points  is given by
is given by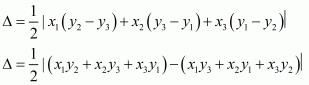
Now Area of ΔABC
Taking three points when A (1, 2) and B (−5, 6) and C (7, −4)

Also,
Now Area of ΔACD
Taking three points when A (1, 2) and C (7, −4) and D (k, −2)

Hence

Question 4: The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Answer :
GIVEN: The vertices of triangle ABC are A (−2, 1) and B (5, 4) and C (2, −3)
TO FIND: The area of triangle ABC and length if the altitude through A
PROOF: We know area of triangle formed by three points 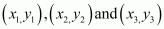 is given by
is given by 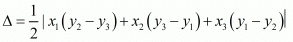
Now Area of ΔABC
Taking three points A (−2, 1) and B (5, 4) and C(2, −3)

We have
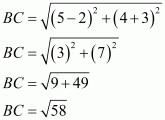
Now,

Question 5: Show that the following sets of points are collinear.
(a) (2, 5), (4, 6) and (8, 8)
(b) (1, −1), (2, 1) and (4, 5)
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
We know area of triangle formed by three points 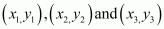 is given by
is given by 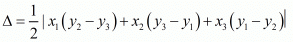
If three points are collinear the area encompassed by them is equal to 0.
The three given points are A(2, 5), B(4, 6) and C(8, 8). Substituting these values in the earlier mentioned formula we have,
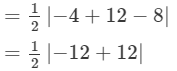

= 0
Since the area enclosed by the three points is equal to 0, the three points need to be . The three given points are A(1, −1), B(2, 1) and C(4, 5). Substituting these values in the earlier mentioned formula we have,
. The three given points are A(1, −1), B(2, 1) and C(4, 5). Substituting these values in the earlier mentioned formula we have,
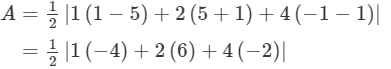

= 0
Since the area enclosed by the three points is equal to 0, the three points need to be .
.
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
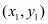 ,
,  and
and 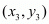 is given by the formula,
is given by the formula,















