Coordinate Geometry Exercise 14.1 (Part-15) | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 51: Find the value of a so that the point (3, a) lies on the line represented by 2x − 3y + 5 = 0
Answer :
If a point 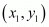 is said lie on a line represented by
is said lie on a line represented by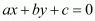 , then the given equation of the line should hold true when the values of the co-ordinates of the points are substituted in it.
, then the given equation of the line should hold true when the values of the co-ordinates of the points are substituted in it.
Here it is said that the point (3, a) lies on the line represented by the equation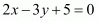 .
.
Substituting the co-ordinates of the values in the equation of the line we have,
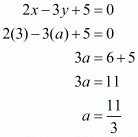
Thus the value of ‘a’ satisfying the given conditions is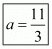 .
.
Question 52: What is the distance between the points A (c, 0) and B (0, −c)?
Answer :
We have to find the distance between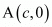 and
and 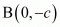 .
.
In general, the distance between A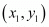 and B
and B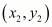 is given by,
is given by,
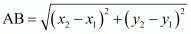
So,

Question 53: If P (2, 6) is the mid-point of the line segment joining A (6, 5) and B (4, y), find y.
Answer :
It is given that mid-point of line segment joining A (6, 5) and B (4, y) is P (2, 6)
In general to find the mid-point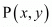 of two points
of two points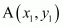 and
and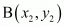 we use section formula as,
we use section formula as,
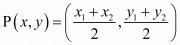
So,
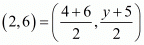
Now equate the y component to get,
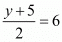
So,
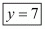
Question 54: If the distance between the points (3, 0) and (0, y) is 5 units and y is positive. then what is the value of y?
Answer :
It is given that distance between P (3, 0) and 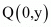 is 5.
is 5.
In general, the distance between A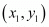 and B
and B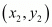 is given by,
is given by,
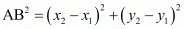
So,
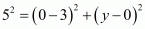
On further simplification,
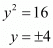
We will neglect the negative value. So,
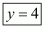
Question 55: If P (x, 6) is the mid-point of the line segment joining A (6, 5) and B (4, y), find y.
Answer :
It is given that mid-point of line segment joining A (6, 5) and B (4, y) is 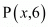
In general to find the mid-point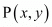 of two points
of two points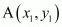 and
and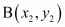 we use section formula as,
we use section formula as,
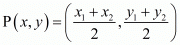
So,

Now equate the y component to get,
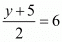
So,
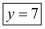
Question 56: If P (2, p) is the mid-point of the line segment joining the points A (6, −5) and B (−2, 11). find the value of p.
Answer :
It is given that mid-point of line segment joining A (6,−5) and B (−2, 11) is 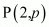
In general to find the mid-point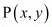 of two points
of two points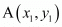 and
and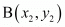 we use section formula as,
we use section formula as,
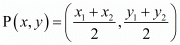
So,
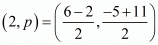
Now equate the y component to get,

Question 57: If A (1, 2) B (4, 3) and C (6, 6) are the three vertices of a parallelogram ABCD, find the coordinates of fourth vertex D.
Answer :
Let ABCD be a parallelogram in which the co-ordinates of the vertices are A (1, 2);
B (4, 3) and C (6, 6). We have to find the co-ordinates of the forth vertex.
Let the forth vertex be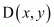
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide.
Now to find the mid-point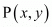 of two points
of two points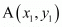 and
and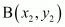 we use section formula as,
we use section formula as,

The mid-point of the diagonals of the parallelogram will coincide.
So,
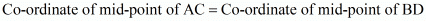
Therefore,
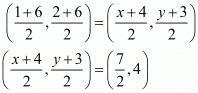
Now equate the individual terms to get the unknown value. So,
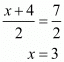
Similarly,

So the forth vertex is 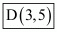
Question 58: What is the distance between the points A(sinθ−cosθ,0) and B(0,sinθ+cosθ)?
Answer : The given points are A(sinθ−cosθ,0) and B(0,sinθ+cosθ).
Using distance formula, we have

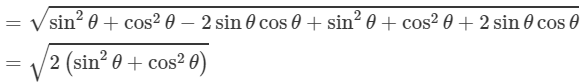
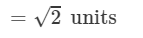 (sin2θ+cos2θ=1)
(sin2θ+cos2θ=1)
Thus, the distance between the given points is √2 units.
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















