Co­ordinate Geometry Exercise 14.1 (Part-4) | Extra Documents, Videos & Tests for Class 10 PDF Download

Question 46: If the point P(x, 3) is equidistant from the point A(7, −1) and B(6, 8), then find the value of x and find the distance AP.

Answer : It is given that P(x, 3) is equidistant from the point A(7, −1) and B(6, 8). 

AP = BP 

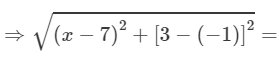
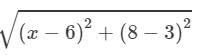   (Distance formula) 

Squaring on both sides, we get
(x−7)2+16=(x−6)2+25⇒x2−14x+49+16=x2−12x+36+25⇒−14x+12x=61−65⇒−2x=−4⇒x=2

Thus the value of x is 2.

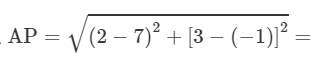
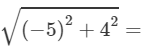
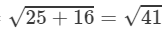   units 

Question 47: If A(3, y) is equidistant from points P(8, −3) and Q(7, 6), find the value of y and find the distance AQ.

Answer :

It is given that A(3, y) is equidistant from points P(8, −3) and Q(7, 6).
∴ AP = AQ 

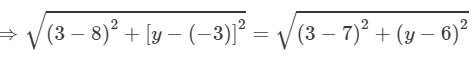  (Distance formula) 

Squaring on both sides, we get 

25+(y+3)2=16+(y−6)2⇒25+y2+6y+9=16+y2−12y+36⇒12y+6y=52−34⇒18y=18⇒y=1

Thus, the value of y is 1. 

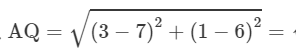
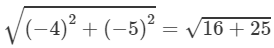
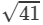= units

Question 48: If (0, −3) and (0, 3) are the two vertices of an equilateral triangle, find the coordinates of its third vertex. 

Answer :Let the given points be A(0, −3) and B(0, 3). Suppose the coordinates of the third vertex be C(x, y).
Now, ∆ABC is an equilateral triangle.
∴ AB = BC = CA  

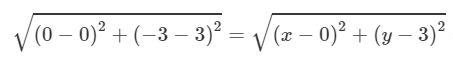
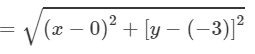
(Distance formula)
Squaring on both sides, we get 

36=x2+(y−3)2=x2+(y+3)236=x2+y-32=x2+y+32

⇒ x2+(y−3)2=x2+(y+3)2x2+y-32=x2+y+32 and x2+(y−3)2=36x2+y-32=36

Now, 

x2+(y−3)2=x2+(y+3)2⇒y2−6y+9=y2+6y+9⇒−12y=0⇒y=0

Putting y = 0 in x2+(y−3)2=36x2+y-32=36, we get 

x2+(0−3)2=36⇒x2=36−9=27⇒x=±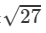=±3√3Thus, the coordinates of the third vertex are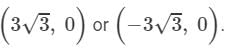 

Question 49:If the point P(2, 2) is equidistant from the points A(−2, k) and B(−2k, −3), find k. Also, find the length of AP.  

Answer :

It is given that P(2, 2) is equidistant from the points A(−2, k) and B(−2k, −3).
∴ AP = BP 

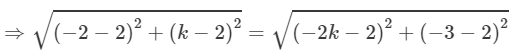 (Distance formula) 

Squaring on both sides, we get 

16+k2−4k+4=4k2+8k+4+25⇒3k²+12k+9=0

⇒k²+4k+3=0

⇒(k+3)(k+1)=0

⇒k+3=0 or k+1=0

⇒k=−3 or k=−1 

Thus, the value of k is −1 or −3.

When k = −1,

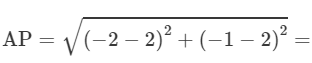
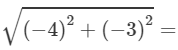
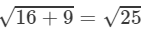  = 5 units

When k = −3, 

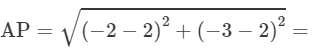
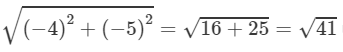  units 

Question 50: An equilateral triangle has two vertices at the points (3, 4) and (−2, 3), find the coordinates of the third vertex.

Answer :

The distance d between two points 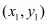 and 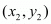 is given by the formula

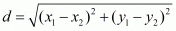
In an equilateral triangle all the sides are of equal length.

Here we are given that A (3, 4) and B (−2, 3) are two vertices of an equilateral triangle. Let C(x, y) be the third vertex of the equilateral triangle.

First let us find out the length of the side of the equilateral triangle.

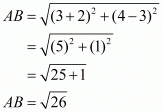
Hence the side of the equilateral triangle measures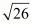 units.

Now, since it is an equilateral triangle, all the sides need to measure the same length.

Hence we have

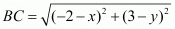
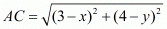
Equating both these equations we have,

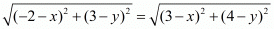
Squaring on both sides we have,

From the above equation we have,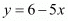

Substituting this and the value of the side of the triangle in the equation for one of the sides we have,

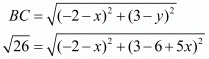
Squaring on both sides,

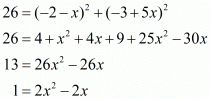
Now we have a quadratic equation for ‘x’. Solving for the roots of this equation,

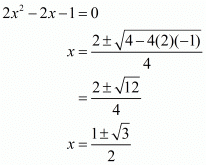
We know that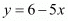. Substituting the value of ‘x’ we have,

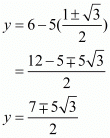
Hence the two possible values of the third vertex are.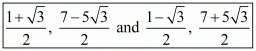

Question 51: Find the circumcentre of the triangle whose vertices are (−2, −3), (−1, 0), (7, −6).

Answer : 

The distance d between two points 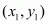 and 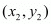 is given by the formula

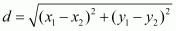
The circumcentre of a triangle is the point which is equidistant from each of the three vertices of the triangle.

Here the three vertices of the triangle are given to be A(−2.−3), B(−1,0) and C(7,−6).

Let the circumcentre of the triangle be represented by the point R(x, y).

So we have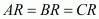 

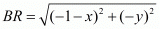
Equating the first pair of these equations we have,

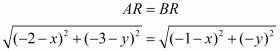
Squaring on both sides of the equation we have,

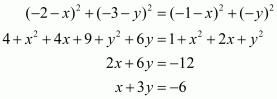
Equating another pair of the equations we have,

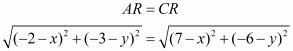
Squaring on both sides of the equation we have,

Now we have two equations for ‘x’ and ‘y’, which are

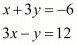
From the second equation we have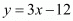. Substituting this value of ‘y’ in the first equation we have,

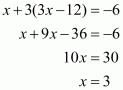
Therefore the value of ‘y’ is,

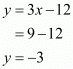
Hence the co−ordinates of the circumcentre of the triangle with the given vertices are.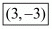

Question 52: Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).

Answer :

The distance d between two points 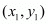 and  is given by the formula

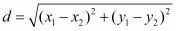
In a right angled triangle the angle opposite the hypotenuse subtends an angle of.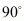

Here let the given points be A(0,100), B(10,0). Let the origin be denoted by O(0,0).

Let us find the distance between all the pairs of points

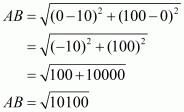
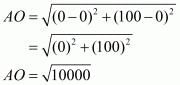
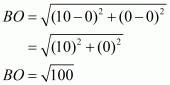
Here we can see that.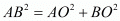

So, 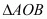 is a right angled triangle with ‘AB’ being the hypotenuse. So the angle opposite it has to be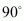. This angle is nothing but the angle subtended by the line segment ‘AB’ at the origin.

Hence the angle subtended at the origin by the given line segment is.

Question 53: Find the centre of the circle passing through (5, −8), (2, −9) and (2, 1).

Answer :

The distance d between two points 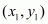 and 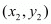 is given by the formula

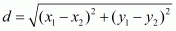
The centre of a circle is at equal distance from all the points on its circumference.

Here it is given that the circle passes through the points A(5,−8), B(2,−9) and C(2,1).

Let the centre of the circle be represented by the point O(x, y).

So we have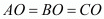 

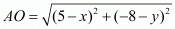
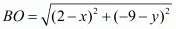
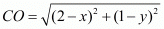
Equating the first pair of these equations we have,

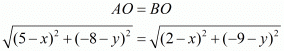
Squaring on both sides of the equation we have,

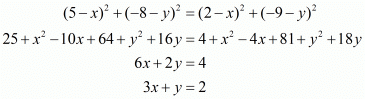
Equating another pair of the equations we have,

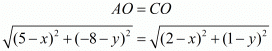
Squaring on both sides of the equation we have,

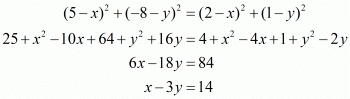
Now we have two equations for ‘x’ and ‘y’, which are

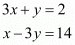
From the second equation we have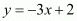. Substituting this value of ‘y’ in the first equation we have,

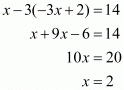
Therefore the value of ‘y’ is,

Hence the co-ordinates of the centre of the circle are.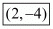

Question 54: If two opposite vertices of a square are (5, 4) and (1, −6), find the coordinates of its remaining two vertices.

Answer :

The distance d between two points  and 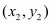 is given by the formula

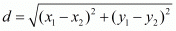
In a square all the sides are of equal length. The diagonals are also equal to each other. Also in a square the diagonal is equal to 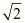 times the side of the square.

Here let the two points which are said to be the opposite vertices of a diagonal of a square be A(5,4) and C(1,−6).

Let us find the distance between them which is the length of the diagonal of the square.

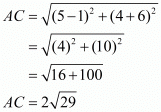
Now we know that in a square,

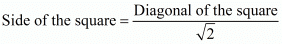
Substituting the value of the diagonal we found out earlier in this equation we have,

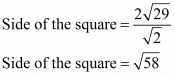
Now, a vertex of a square has to be at equal distances from each of its adjacent vertices.

Let P(x, y) represent another vertex of the same square adjacent to both ‘A’ and ‘C’.

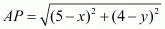
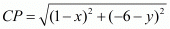
But these two are nothing but the sides of the square and need to be equal to each other.

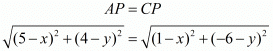
Squaring on both sides we have,

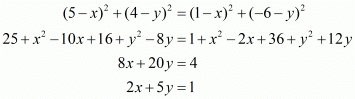
From this we have,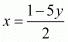 

Substituting this value of ‘x’ and the length of the side in the equation for ‘AP’ we have,

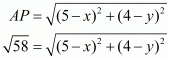
Squaring on both sides,

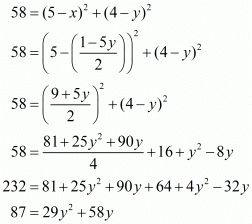
We have a quadratic equation. Solving for the roots of the equation we have,

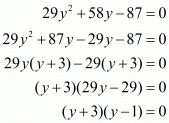
The roots of this equation are −3 and 1.

Now we can find the respective values of ‘x’ by substituting the two values of ‘y’

When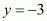 

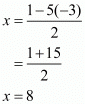
When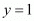 

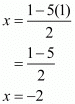
Therefore the other two vertices of the square are.

Question 55: Find the centre of the circle passing through (6, −6), (3, −7) and (3, 3).

Answer :

The distance d between two points 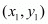 and 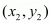 is given by the formula

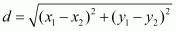
The centre of a circle is at equal distance from all the points on its circumference.

Here it is given that the circle passes through the points A(6,−6), B(3,−7) and C(3,3).

Let the centre of the circle be represented by the point O(x, y).

So we have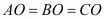 

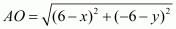
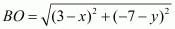
Equating the first pair of these equations we have,

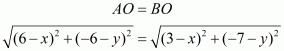
Squaring on both sides of the equation we have,

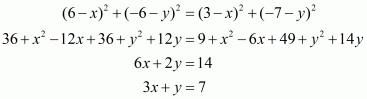
Equating another pair of the equations we have,

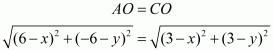
Squaring on both sides of the equation we have,

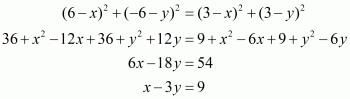
Now we have two equations for ‘x’ and ‘y’, which are

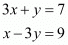
From the second equation we have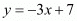. Substituting this value of ‘y’ in the first equation we have,

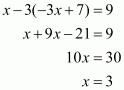
Therefore the value of ‘y’ is,

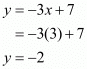
Hence the co-ordinates of the centre of the circle are.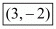

Question 56: Two opposite vertices of a square are (−1, 2) and (3, 2). Find the coordinates of other two vertices.

Answer :

The distance d between two points 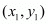 and 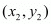 is given by the formula

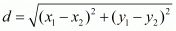
In a square all the sides are of equal length. The diagonals are also equal to each other. Also in a square the diagonal is equal to 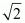 times the side of the square.

Here let the two points which are said to be the opposite vertices of a diagonal of a square be A(−1,2) and C(3,2).

Let us find the distance between them which is the length of the diagonal of the square.

Now we know that in a square,

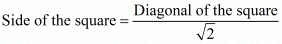
Substituting the value of the diagonal we found out earlier in this equation we have,

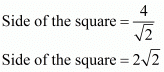
Now, a vertex of a square has to be at equal distances from each of its adjacent vertices.

Let P(x, y) represent another vertex of the same square adjacent to both ‘A’ and ‘C’.

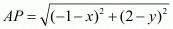
But these two are nothing but the sides of the square and need to be equal to each other.

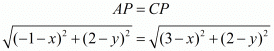
Squaring on both sides we have,

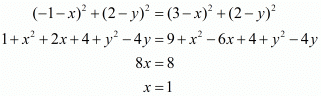
Substituting this value of ‘x’ and the length of the side in the equation for ‘AP’ we have,

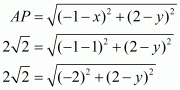
Squaring on both sides,

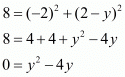
We have a quadratic equation. Solving for the roots of the equation we have,

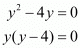
The roots of this equation are 0 and 4.

Therefore the other two vertices of the square are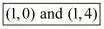.k+1=0⇒k=-3 or k=-