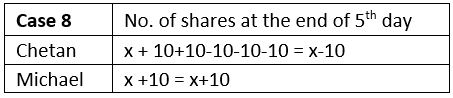Data Caselets: Introduction & Solved Examples | CSAT Preparation - UPSC PDF Download
| Table of contents |

|
| What are Caselets? |

|
| 1. Paragraph Based on Reasoning |

|
| 2. Paragraph Based on Numerical Data |

|
| Tips to Solve Data Caselet Questions |

|
| Solved Questions for You |

|
What are Caselets?
- In caselets, data is given in the form of paragraphs. —there are no ready-made tables, charts, or graphs. Their length and detail can vary widely.
- Caselets vary considerably in length, in the amount of information contained, in different sentences and paragraphs.
- While reading a caselet, it's always advisable to underline the important facts and figures and if necessary, make your table/chart/graphs for solving the questions.

Caselet can be of two forms:
- Paragraph based on Reasoning.
- Paragraph based on numerical Data.
Now to understand how to interpret the data we will use examples and try to find a step-wise solution that may help to solve Caselet questions in the exam. Before hopping on to examples keep in mind the following points that will assist you while devising a solution to the problem of Caselet.
- Read the paragraph carefully and recognize the variables around which the whole paragraph revolves and questions are asked. Note down all the important points.
- Try to formulate relationships between the variables pictographically using tables, symbols or Venn diagrams. Tables help to define multivariate relationships more clearly so try using them more often.
- Data interpretation usually requires numerical and arithmetic calculations such as averages, ratios, percentages, etc. Be thorough with their concepts and use shortcuts and tricks for faster calculations, it will save you a lot of time.
- Do not assume information that is not given and use logic and reasoning to find out the hidden information that is given in the paragraph.
- Do not indulge in troublesome lengthy calculations when approximations or relative values are asked. Calculate only what is asked.
1. Paragraph Based on Reasoning
Now let’s move on to an example first of paragraph based on reasoning. Consider the question given below.
In a sports event, six teams (A, B, C, D, E, and F) are competing against each other. Matches are scheduled in two stages. Each team plays three matches in stage – I and two matches in Stage – II. No team plays against the same team more than once in the event. No ties are permitted in any of the matches. The observations after the completion of Stage – I and Stage – II are as given below.
Stage-I:
One team won all three matches.
- Two teams lost all the matches.
- D lost to A but won against C and F.
- E lost to B but won against C and F.
- B lost at least one match.
- F did not play against the top team of Stage-I.
Stage-II:
The leader of Stage-I lost the next two matches.
- Of the two teams at the bottom after Stage-l, one team won both matches, while the other lost both matches.
- One more team lost both matches in Stage-II.
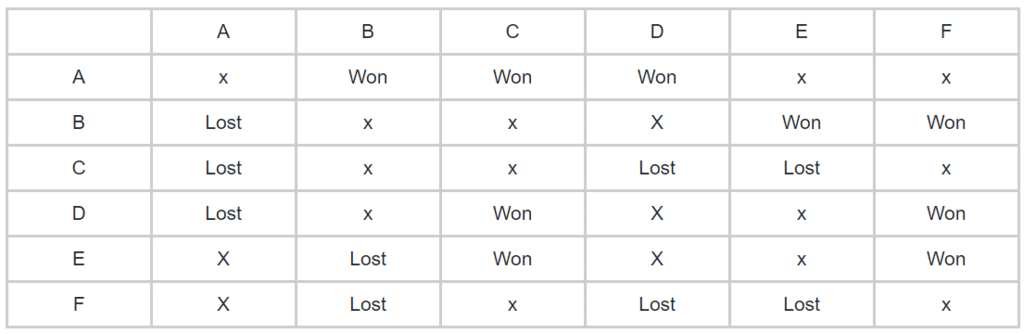
Q1: The two teams that defeated the leader of Stage-I are:
(1) F & D
(2) E & F
(3) B & D
(4) E & D
(5) F & D
Q2: The only team(s) that won both matches in Stage-II is (are)
(1) B
(2) E & F
(3) A, E & F
(4) B, E & F
(5) B & F
Q3: The teams that won exactly two matches in the event are
(1) A, D & F
(2) D & E
(3) E & F
(4) D, E & F
(5) D & F
Q4: The team(s) with the most wins in the event is (are):
(1) A
(2) A & C
(3) F
(4) E
(5) B & E
Step-by-Step Solution
Now let us devise a step-wise solution to the above question. First, we will note down all key points given in the question.
- There are 6 teams: A, B, C, D, E, and F.
- There are 3 matches in stage 1 and 2 matches in stage 2.
- Each team plays against the other once only. There are no ties in the game.
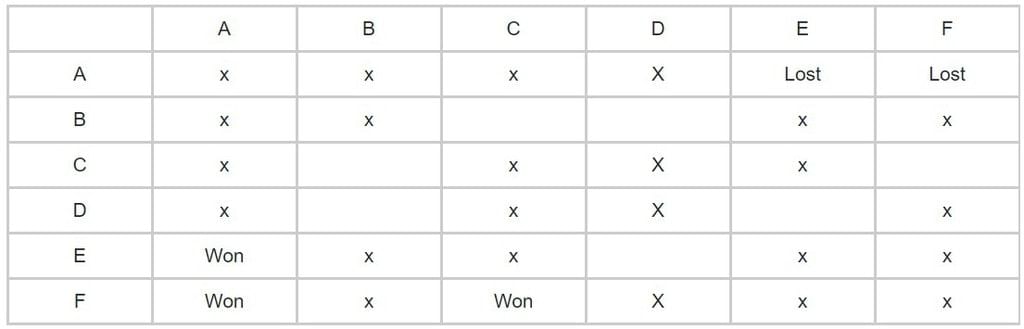
Keeping these points in mind and using the information given about stage 1 we will construct a table for it.
One by one we will interpret all the points given in stage 1 and use x to denote no match between two teams and won & loss for signifying winning and losing teams. The first statement is:
- One team won all 3 matches. But at this moment we have no other information about which team has lost or won so we will get back to this point later.
- Two teams lost all matches. Though it is a useful piece of information as out of 6 teams 2 lost all but we have no further info about which team hence we will move on.
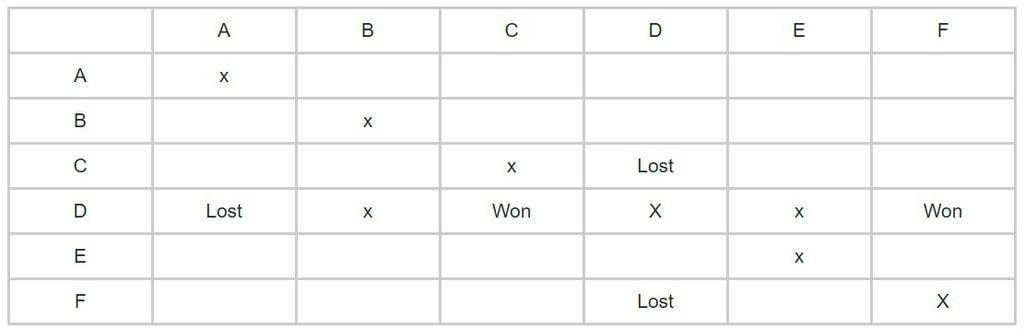
Next, we are given D lost to A. Thus, we will write lost in row 5 and column 1. Also, we will rule out D as the team that won all matches. Also, it won against C and F.
Since no team can play against each other. Therefore, we have put x there. Also as all teams play only 3 matches. There will be no match between D & B and D & E.
Again, as given E lost to B but won against C & F. Therefore, E is also ruled out of the one who won all matches or lost all matches. Thus, there would be no match of E & A and E & D.
Given B has lost at least one match. Therefore, B is not all winning team. And B will not be the losing team too. Since, all B, C, D, E, and F has lost one match at least thus, A is the only team left and hence became the all winning team.
- F doesn’t play against the winning team i.e. A.
- Thus, C and F becomes all losing team. And this will be the table formed.
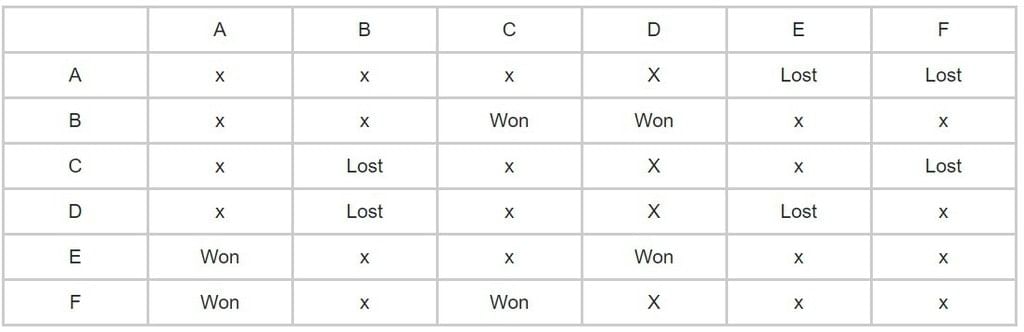
Now we will move on to stage 2 and move on to form a table.
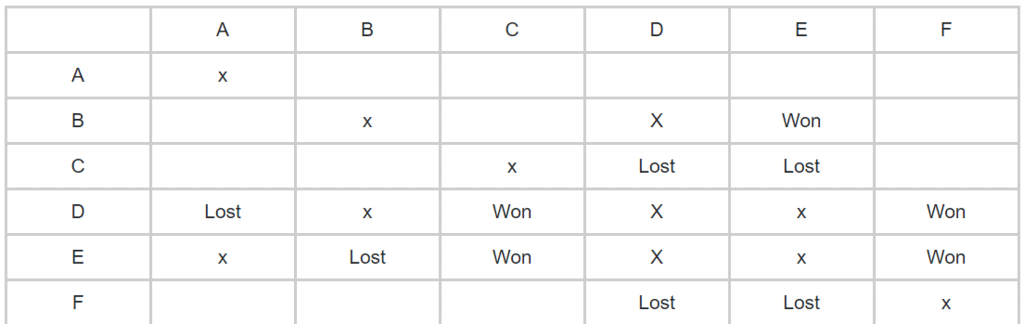
- We are given that no team plays against the same team more than once in the event. So we put an x under all the teams who have played against each other in Stage 1.
- Given leader in stage 1 lost 2 matches. Since A is the leader, A will be the one who will have lost all matches in the next stage. Also, each team has a just single match against the other, therefore, A will lose against E and F.
- Now out of the two losing teams, one won the next two matches and one lost all. Since F won against A. Therefore, F will be the winning team and C, the losing team.
Also given another team lost both matches and it can’t be E again as it won against A and it can neither be B as C to lose both matches require B to win against him. Therefore, D lost both too.
Now we are in a position to answer any question regarding this problem. Hence, we can simply look at these tables and answer the above question easily. Using a similar approach, we can solve many such Caselet reasoning questions.
2. Paragraph Based on Numerical Data
Now let’s move on to an example of paragraph based on numerical data. Consider the question given below.
Two traders, Chetan and Michael, were involved in the buying and selling of MCS shares over five trading days. At the beginning of the first day, the MCS share was priced at Rs. 100, while at the end of the fifth day it was priced at Rs. 110. At the end of each day, the MCS share price either went up by Rs.10, or else, it came down by Rs.10. Both Chetan and Michael took buying and selling decisions at the end of each trading day. The beginning price of the MCS share on a given day was the same as the ending price of the previous day. Chetan and Michael started with the same number of shares and amount of cash and had enough of both. Below are some additional facts about how Chetan and Michael traded over the five trading days.
- Each day if the price went up, Chetan sold 10 shares of MCS at the closing price. On the other hand, each day if the price went down, he bought 10 shares at the closing price.
- If on any day, the closing price was above Rs.110, then Michael sold 10 shares of MCS, while if it was below Rs.90, he bought 10 shares, all at the closing price.
Q1: If Chetan sold 10 shares of MCS on three consecutive days, while Michael sold 10 shares only once during the five days, what was the price of MCS at the end of day 3?
(1) Rs. 90
(2) Rs. 100
(3) Rs. 110
(4) Rs. 120
(5) Rs. 130
Q2: If Chetan ended up with Rs.1300 more cash than Michael at the end of day 5, what was the price of MCS share at the end of day 4?
(1) Rs.90
(2) Rs.100
(3) Rs.110
(4) Rs.120
(5) Not uniquely determinable
Q3: If Michael ended up with 20 more shares than Chetan at the end of day 5, what was the price of the share at the end of day 3?
(1) Rs.90
(2) Rs.100
(3) Rs.110
(4) Rs.120
(5) Rs.130
Q4: If Michael ended up with Rs.100 less cash than Chetan at the end of day 5, what was the difference in the number of shares possessed by Michael and Chetan (at the end of day 5)?
(1) Michael had 10 less shares than Chetan.
(2) Michael had 10 more shares than Chetan.
(3) Chetan had 10 more shares than Michael.
(4) Chetan had 20 more shares than Michael.
(5) Both had the same number of shares.
Step-by-Step Solution
To solve the above caselet and questions on them we will keep all the above-mentioned points and proceed similarly as in the previous example. Again, this time we will construct a table using significant key points.
- In this case, there are two people Michael and Chetan.
- The price at the beginning of the first day is Rs.100 and end of the fifth day is Rs.110.
- Prices fluctuate every day either they went up by Rs.10 or get down by Rs.10. And the ending price of that day becomes the beginning price of next day.
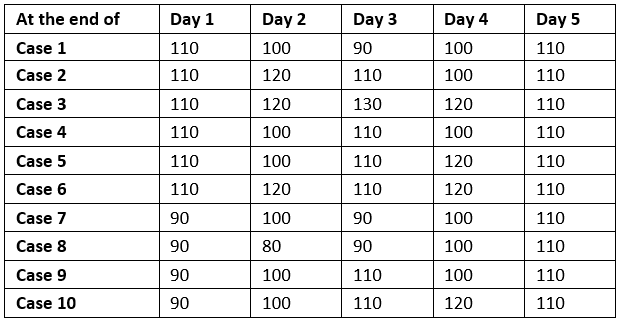
- Using the above points there could be drawn 10 different cases and a table can be constructed like this:
Now with help of two points given in problem about Michael and Chetan and their reaction to decrease and increase in prices. We will directly solve all the following questions of the problem.
Ans 1:
It is being told that Chetan sold 10 shares on 3 consecutive days and Chetan only sells shares if prices went up. Thus, coinciding cases in relevance to Chetan is Case 3, Case 8, Case 10. Also, Michael sold 10 shares only once during all 5 days where Chetan sold thrice. And Michael sells only if the closing price is above 110. Now by comparing all the 3 cases and adding the Michael factor to it, we can easily conclude to solitary case 10. Thus, our solution Case is Case 10. Therefore, the answer to the question is 110.
Ans 2:
If Chetan has 1300 more cash than Michael at the end of the fifth day. The possibility of this happening could be:
Now in all these cases price of the shares at the end of the 4th day is Rs.100.
Ans 3:
Let us assume both Chetan and Michael started with x no. of shares. Now at the end of the 5th day, Michael had 20 more shares than Chetan. We will do similar reasoning as in previous questions but now instead of the amount earned, we will calculate no. of shares.There’s only a single possibility of Michael having 20 more shares than Chetan. Thus, the price at the end of day 3 is Rs.90.
Ans 4:
We need to find out the cases where Michael has Rs.100 less than Chetan. We will proceed as above.
Now as we can see in both case, Michael and Chetan ended up with equal no. of shares. Thus, option (5) is correct.
Tips to Solve Data Caselet Questions
- Create a Table: Make a table to organize the data effectively. Use notations while reading the caselet to fill in the table.
- Read Carefully: Pay close attention to the caselet details to avoid errors. Ensure all data units match and convert any that don't.
- Know the Basics: Understand fundamental arithmetic concepts like unit conversion, percentages, profit and loss, and interests.
- Use Shortcuts and Approximations: Utilize shortcuts and approximations to speed up your problem-solving process. Look for the closest value among options to save time.
- Practice Regularly: Practice basic mathematical topics and example questions related to data caselets to build confidence and proficiency. Solving various types of caselet questions will also prepare you well for the exam.
Solved Questions for You
Example 1: Ghosh Babu took voluntary retirement in Dec. 1991 and received a certain amount of money as retirement benefits. On Jan 1, 1992, he invested the entire amount in shares. At the end of the month, he sold all his shares and realised 25% profit. On Feb 1, he reinvested the entire amount in shares which he sold at the end of the month at a loss of 20%. Again, he invested the entire amount on Mar 1 in a new company. At the end of the month, he sold the new company to a friend and realised a profit of 20% in the process. He invested the entire amount in shares on Apr 1, which he sold at the end of the month for Rs. 1,08,000 incurring a loss of 10%.
Q.1. What is the amount of retirement benefits received by Ghosh Babu?
(a) Rs. 1,08,000
(b) Rs. 1,25,000
(c) Rs. 1,20,000
(d) Rs. 1,00,000
Correct Answer is option (d).
Let the amount received by Ghosh Babu in Dec. 1991 be Rs. x, as retirement benefits:
- Therefore, investment in the month of Jan 1992 = 100
- Profit of 25% at the end of Jan 1992.
- Hence, investment in the month of Feb 1992 = 125
- Loss of 20% at the end of Feb 1992
- Hence, investment in the month of March 1992 = 100
- Profit of 20% at the end of March 1992
- Hence, investment in the month of April 1992 = 120
- Loss of 10% at the end of April 1992
- Therefore the amount left at the end of April 1992 = 108
- Amount at the end of April 1002 = Rs. 1,08,000
- Therefore, simply equating figures, he would have started with Rs 1,00,000
Q.2. The percentage profit received by Ghosh Babu between Jan 1 and Apr 30 is:
(a) 8.00%
(b) 15.00%
(c) - 10.00%
(d) None of these
Correct Answer is option (a).
% Profit between Jan 1 and Apr 30 = (1.08x - x/x) X 100
Q.3. The amount of loss incurred by Ghosh Babu based on his operation in Apr 1992 is:
(a) Rs. 25,000
(b) Rs. 12,000
(c) Rs. 20,000
(d) Rs. 8,000
Correct Answer is option (b).
Investment in the month of April = Rs. 1,20,000
Amount received at end of April = Rs. 1,08,000
Therefore, Loss = Rs. 12,000
Q.4. The maximum amount invested by Ghosh Babu in any one month was in:
(a) January
(b) February
(c) March
(d) April
Correct Answer is option (b).
Maximum amount invested by Ghosh Babu is in the month of February = Rs. 1,25,000
Example 2: 4 colleges A, B, C and D participated in 3 surveys BS, KIRF and GT. All the 4 colleges managed to secure a rank less than 7 in all the 3 surveys. Further, it is known that no 2 colleges were tied for the same position in any of the surveys.
Only A had a better rank than D in the survey conducted by KIRF.
B managed to get a better rank than C in 2 of the 3 surveys.
D was ranked second in the survey conducted by KIRF. It is the only survey in which D managed to bag a rank within the top 3.
GT deemed C to be a better college than A.
The average rank secured by D was 4.
D had a better rank in the survey conducted by BS than the one conducted by GT.
No college had the same rank in 2 surveys.
D was ranked the worst among the 4 colleges in 2 of the 3 surveys.
A managed a position within the top 3 in all 3 surveys.
Q 1: If B was ranked third in the survey conducted by BS and the average ranks of B and C were not equal, then the rank of B in the survey conducted by KIRF is
a) 3
b) 4
c) 5
d) 6
Ans 1: Option 'b' is correct
Sol: No college had the same rank in 2 surveys.
A managed a position within the top 3 in all the surveys.
Only A had a better rank than D in all 3 surveys.
Average rank of D is 4.
=> Sum of the ranks secured by D = 12.
We know that D secured the second rank in the survey by KIRF.
=> Sum of ranks secured by D in the BS and GT surveys = 10.
10 can be represented as (5,5) or (6,4).
We know that no college secured the same rank in 2 surveys.
Therefore, the ranks secured by D must be 6 and 4.
D had a better rank in the survey conducted by BS than the one conducted by GT.
We know that A managed a position within the top 3 in all 3 surveys.
Therefore, A must have secured second and third positions in the other 2 surveys. Also, the average rank secured by A must be 2.
Let us solve each question separately now. The points that one must bear in mind while filling the table are
(1) B managed to get a better rank than C in 2 of the 3 surveys.
(2) GT deemed C to be a better college than A.
B was ranked third in the survey conducted by BS. Also, we know that the average ranks of B and C were not equal.
Now, A must have secured second rank and C must have secured first rank in the survey conducted by BS.
In the other 2 surveys, B must have a better rank than C. A must have secured third rank in the survey conducted by GT.
C must have secured second rank (since GT deems C to be a better college than C) and B must have secured first rank.
Since B has secured third rank in BS rankings, it must have secured the fourth or fifth rank in the KIRF rankings.
Had B secured fifth rank, C must have secured the sixth rank (Since 2 of the 3 surveys place B above C).In this case, the average rank secured by both B and C will be equal (3). Therefore, we can eliminate this possibility.
B must have secured 4th rank and C must have secured sixth rank.
Therefore B is the right answer.
Q 2: If the average rank secured by C is 3 and B is 2 in the 3 surveys, what is the rank secured by C in the survey conducted by KIRF
a) 3
b) 4
c) 5
d) 6
Ans 2: Option 'c' is correct
Sol: We know that no college secured the same rank in 2 surveys.
Therefore, the ranks secured by D must be 6 and 4.
D had a better rank in the survey conducted by BS than the one conducted by GT.
We know that A managed a position within the top 3 in all 3 surveys. Therefore, A must have secured second and third positions in the other 2 surveys. Also, the average rank secured by A must be 2.Let us solve each question separately now. The points that one must bear in mind while filling the table are
(I) B managed to get a better rank than C in 2 of the 3 surveys.
(II) GT deemed C to be a better college than A.
Average rank secured by B is 2 and C is 3.
Therefore, sum of the ranks secured by B and C must be 6 and 9 respectively. Sum of ranks secured by B is 6. Therefore, the ranks must be 1,2 and 3.
B must have secured third rank in the survey conducted by KIRF (Since the first 2 ranks are already taken up).
C had a better rank than A in the survey conducted by GT
Had C secured first rank in the survey conducted by BS, then C must have secured second rank in the survey conducted by GT.
A must have secured third rank in the survey conducted by GT and second rank in the survey conducted by BS. However, B could not have secured third rank in the survey conducted by BS since A has secured third rank. Therefore, this case can be eliminated.
Had C secured first rank in the survey conducted by GT, B must have secured first rank in the survey conducted by BS. A must have secured second rank in the survey conducted by BS and C must have secured the third rank. The rankings will be as follows:As we can see, C must have secured fifth rank in the survey conducted by KIRF.
Therefore, option C is the right answer
Q 3: If the average rank secured by C is the same as the average rank secured by B and the rank secured by A in GT is better than the one it secured in BS, then the rank secured by B in GT survey is
(The average rank secured across the 3 surveys is an integer for all the 4 colleges)
a) 3 or 5
b) 5 or 6
c) 4 or 5
d) 1 or 3
Ans 3: Option 'a' is correct
Sol: We know that no college secured the same rank in 2 surveys.
Therefore, the ranks secured by D must be 6 and 4.
D had a better rank in the survey conducted by BS than the one conducted by GT.
We know that A managed a position within the top 3 in all 3 surveys. Therefore, A must have secured second and third positions in the other 2 surveys. Also, the average rank secured by A must be 2.Let us solve each question separately now. The points that one must bear in mind while filling the table are
(I) B managed to get a better rank than C in 2 of the 3 surveys.
(II) GT deemed C to be a better college than A.
Average rank secured by B and C is the same.
Average rank secured by B and C cannot be 2 since in KIRF one of the 2 must have secured a rank greater than 3.
Average rank cannot be 6 as well.
Average rank cannot be 5 since both of them have a rank less than 4 in the BS survey.
Let us consider the possibility that the average rank is 4.
Therefore, sum of ranks must be 12.
Also, we know that rank secured by A in GT is better than the one it secured in the survey by BS.
Therefore, A must have secured second rank in GT and third rank in BS.
In the BS survey, B and C must have secured first and second ranks, respectively.
Since C is ranked better than A by GT, C must have secured the first rank in the GT survey.
Now, C must have secured a rank of 8 in the KIRF ranking for the average rank to be 4. As
we can see, this case is impossible.
Therefore, the average rank of both B and C must be 3.
C must have secured first rank in the GT survey and second rank in the BS survey.
For the average rank to be 6, C must have secured sixth rank in the KIRF survey.
B must have secured first rank in the BS survey.
Now, the sum of the ranks secured by B in the other 2 surveys must be 9-1 = 8.
8 can be represented as (4,4), (5,3) or (6,2).
We can eliminate the case (4,4) since no college secured the same ranking in 2 colleges.
We can eliminate (6,2) too since no 2 colleges secured the same ranking in a survey.
Therefore, the final ranking will be as follows:Rank secured by B in GT is 3 or 5.
Therefore , option A is correct
|
205 videos|264 docs|136 tests
|
FAQs on Data Caselets: Introduction & Solved Examples - CSAT Preparation - UPSC
| 1. What are the different types of caselets? |  |
| 2. How can I improve my skills in solving data caselet questions? |  |
| 3. What is the importance of caselets in competitive exams like CAT? |  |
| 4. Can you suggest some tips for solving caselet questions effectively? |  |
| 5. Where can I find solved examples of caselet problems for practice? |  |