Definition: Stress | Fluid Mechanics for Mechanical Engineering PDF Download
| Table of contents |

|
| What is Stress? |

|
| Definition of Fluid |

|
| Concept of Continuum |

|
| Fluid Properties |

|
| Causes of Viscosity |

|
| No-Slip Condition of Viscous Fluids |

|
What is Stress?
- When the deforming force is applied to an object, the object deforms.
- In order to bring the object back to its original shape and size, there will be an opposing force generated inside the object.
- This restoring force will be equal in magnitude and opposite in direction to the applied deforming force.
- The measure of this restoring force generated per unit area of the material is called stress.
Thus, Stress is defined as “The restoring force per unit area of the material”. It is a tensor quantity. Denoted by the Greek letter σ. Measured using Pascal or N/m2. Mathematically expressed as:
σ = F/A
- F is the restoring force measured in Newtons or N.
- A is the area of the cross-section measured in m2.
- σ is the stress measured using N/m2 or Pa.
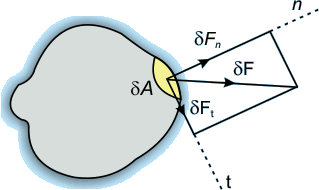 Normal and Tangential Forces on a Surface
Normal and Tangential Forces on a Surface
Consider a small area δA on the surface of a body, and the force acting on this area is δF.
This force can be resolved into two perpendicular components:
- The component of force acting normal to the area is called the normal force and is denoted by δFn.
- The component of force acting along the plane of the area is called the tangential force and is denoted by δFt.
When they are expressed as force per unit area, they are called normal stress and tangential stress, respectively. Tangential stress is also called shear stress.
- Normal stress:

- Shear stress:

Definition of Fluid
A fluid is a substance that deforms continuously in the face of tangential or shear stress, irrespective of the magnitude of shear stress. This continuous deformation under the application of shear stress constitutes a flow.
In this connection, fluid can also be defined as a state of matter that cannot sustain any shear stress.
Example: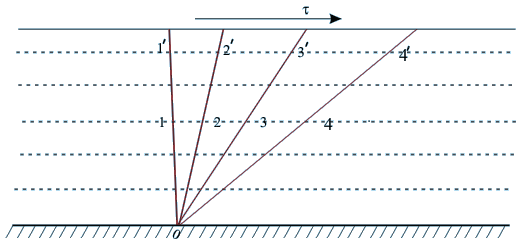 Shear Stress on a Fluid Body
Shear Stress on a Fluid BodyIf a shear stress τ is applied at any location in a fluid, the element 011', which is initially at rest, will move to 022', then to 033'. Further, it moves to 044' and continues to move similarly.
- In other words, the tangential stress in a fluid body depends on the velocity of deformation and vanishes as this velocity approaches zero.
- A good example is Newton's parallel plate experiment, where the dependence of shear force on the velocity of deformation was established.
The Distinction Between Solid and Fluid
 Deformation of a Solid Body
Deformation of a Solid Body
Concept of Continuum
- The concept of the continuum is a kind of idealization of the continuous description of matter, where the properties of the matter are considered as continuous functions of space variables.
- Although any matter is composed of several molecules, the concept of continuum assumes a continuous distribution of mass within the matter or system with no empty space, instead of the actual conglomeration of separate molecules.
- Describing a fluid flow quantitatively makes it necessary to assume that flow variables (pressure, velocity, etc.) and fluid properties vary continuously from one point to another. Mathematical description of flow on this basis has proved to be reliable and treatment of fluid medium as a continuum has firmly become established.
Example: Density at a point is normally defined as
Here, Δ∀ is the volume of the fluid element and m is the mass. If Δ∀ is very large, ρ is affected by the inhomogeneities in the fluid medium. Considering another extreme if Δ∀ is very small, random movement of atoms (or molecules) would change their number at different times.
In the continuum approximation point, density is defined at the smallest magnitude of Δ∀, before statistical fluctuations become significant. This is called the continuum limit and is denoted by Δ∀c.
- One of the factors considered important in determining the validity of the continuum model is molecular density. It is the distance between the molecules that is characterized by the mean free path ( λ ). It is calculated by finding the statistical average distance the molecules travel between two successive collisions. If the mean free path is very small as compared with some characteristic length in the flow domain (i.e., the molecular density is very high), then the gas can be treated as a continuous medium. If the mean free path is large in comparison to some characteristic length, the gas cannot be considered continuous and it should be analyzed by the molecular theory.
- A dimensionless parameter is known as the Knudsen number, Kn = λ / L, where λ is the mean free path and L is the characteristic length. It describes the degree of departure from the continuum.
Usually, when Kn > 0.01, the concept of the continuum does not hold good.
Beyond this critical range of Knudsen number, the flows are known as slip flow (0.01 < Kn < 0.1), transition flow (0.1 < Kn < 10) and free-molecule flow (Kn > 10).
However, for the flow regimes considered in this course, Kn is always less than 0.01 and it is usual to say that the fluid is a continuum. - Another factor that checks the validity of the continuum is the elapsed time between collisions. The time should be small enough so that the random statistical description of molecular activity holds good.
- In the continuum approach, fluid properties such as density, viscosity, thermal conductivity, temperature, etc. can be expressed as continuous functions of space and time.
Fluid Properties
Characteristics of a continuous fluid that are independent of the motion of the fluid are called basic properties of the fluid.
Some of the basic properties are discussed below:
(a) Density (kg/m3)
(i) Symbol: ρ
(ii) Definition: The density ρ of a fluid is its mass per unit volume. If a fluid element enclosing a point P has a volume Δ∀ and mass m, then the density at point P is written as:

However, in a medium where the continuum model is valid, one can write:
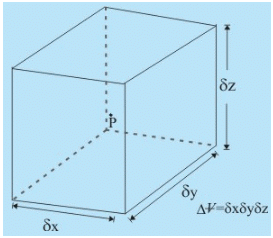 A fluid element enclosing point P
A fluid element enclosing point P
(b) Specific Weight (N/m3)
(i) Symbol: Y
(ii) Definition: The specific weight is the weight of fluid per unit volume.
The specific is given:
 where g is the gravitational acceleration. Just as weight must be clearly distinguished from mass, so must the specific weight be distinguished from density.
where g is the gravitational acceleration. Just as weight must be clearly distinguished from mass, so must the specific weight be distinguished from density.(c) Specific Volume (m3/Kg)
(i) Symbol: v
(ii) Definition: The specific volume of a fluid is the volume occupied by unit mass of fluid. Thus,

(d) Specific Gravity
(i) Symbol: s
(ii) Definition:
- For liquids, it is the ratio of the density of a liquid at the actual condition to the density of pure water at 101 kN/m2 and at 4˚C.
- For gases, is the ratio of its density to that of either hydrogen or air at some specified temperature or pressure.
- However, there is no general standard; so the conditions must be stated while referring to the specific gravity of a gas.
(e) Viscosity
(i) Symbol: μ
(ii) Definition:
Viscosity is a fluid property whose effect is understood when the fluid is in motion.
In a flow of fluid, when the fluid elements move with different velocities, each element will feel some resistance due to fluid friction within the elements.
Therefore, shear stresses can be identified between the fluid elements with different velocities.
The relationship between the shear stress and the velocity field was given by Sir Isaac Newton.
Consider a flow in which all fluid particles are moving in the same direction in such a way that the fluid layers move parallel with different velocities: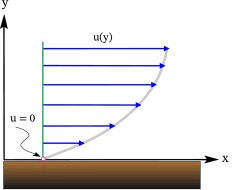 A Parallel Flow of a fluid
A Parallel Flow of a fluid
 Two adjacent layers of moving fluid
Two adjacent layers of moving fluid
- The upper layer, which is moving faster, tries to draw the lower slowly moving layer along with it by means of a force F along the direction of flow on this layer. Similarly, the lower layer tries to retard the upper one, according to Newton's third law, with an equal and opposite force F on it.
- Such a fluid flow where x-direction velocities, i.e. change with y-coordinate is called the shear flow of the fluid.
- Thus, the dragging effect of one layer on the other is experienced by a tangential force F on the respective layers. If F acts over an area of contact A, then the shear stress τ is defined as, τ = F/A.
- Newton postulated that τ is proportional to the quantity Δu/ Δy where Δy is the distance of separation of the two layers and Δu is the difference in their velocities.
- In the limiting case of, Δu / Δy equals du/dy, the velocity gradient at a point in a direction perpendicular to the direction of the motion of the layer.
- According to Newton τ and du/dy bears the relation,
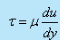 where the constant of proportionality μ is known as the coefficient of viscosity or simply viscosity which is a property of the fluid and depends on its state.
where the constant of proportionality μ is known as the coefficient of viscosity or simply viscosity which is a property of the fluid and depends on its state. - The sign of τ depends upon the sign of du/dy. For the profile shown in the above fig, du/dy is positive everywhere and hence, τ is positive. Both the velocity and stress are considered positive in the positive direction of the coordinate parallel to them.
- Equation
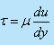 , defining the viscosity of a fluid, is known as Newton's law of viscosity.
, defining the viscosity of a fluid, is known as Newton's law of viscosity.
 View Answer
View Answer 
Note:
Common fluids, viz. water, air, mercury obey Newton's law of viscosity and are known as Newtonian fluids.
Other classes of fluids, viz. paints, different polymer solution, blood do not obey the typical linear relationship, of τ and du/dy and are known as non-Newtonian fluids.
In non-newtonian fluids viscosity, itself may be a function of deformation rate as you will study in the next lecture.
Causes of Viscosity
- The causes of viscosity in a fluid are possibly attributed to two factors:
(i) Intermolecular force of cohesion.
(ii) Molecular momentum exchange. - Due to strong cohesive forces between the molecules, any layer in a moving fluid tries to drag the adjacent layer to move with an equal speed and thus produces the effect of viscosity as discussed earlier. Since cohesion decreases with temperature, the liquid viscosity does likewise.
 Movement of Fluid molecules between two adjacent moving layers
Movement of Fluid molecules between two adjacent moving layers
- Molecules from layer aa in the course of continuous thermal agitation migrate into layer bb. Momentum from the migrant molecules from layer aa is stored by molecules of layer bb by way of collision. Thus, layer bb as a whole is speeded up.
- Molecules from the lower layer bb arrive at aa and tend to retard the layer aa. Every such migration of molecules causes forces of acceleration or deceleration to drag the layers so as to oppose the differences in velocity between the layers and produce the effect of viscosity.
- As the random molecular motion increases with a rise in temperature, the viscosity also increases accordingly. Except for very special cases,
Example: At very high pressure, the viscosity of both liquids and gases ceases to be a function of pressure. - For Newtonian fluids, the coefficient of viscosity depends strongly on temperature but varies very little with pressure.
- For liquids, molecular motion is less significant than the forces of cohesion; thus the viscosity of liquids decreases with an increase in temperature.
- For gases, molecular motion is more significant than the cohesive forces, thus the viscosity of gases increases with an increase in temperature.
 Change of viscosity of water and air under 1 atm
Change of viscosity of water and air under 1 atm
No-Slip Condition of Viscous Fluids
- It has been established through experimental observations that the relative velocity between the solid surface and the adjacent fluid particles is zero whenever a viscous fluid flows over a solid surface. This is known as the no-slip condition.
- This behaviour of no-slip at the solid surface is not the same as the wetting of surfaces by the fluids.
Example: Mercury flowing in a stationary glass tube will not wet the surface but will have zero velocity at the wall of the tube. - The wetting property results from surface tension, whereas the no-slip condition is a consequence of fluid viscosity.
|
56 videos|146 docs|75 tests
|
FAQs on Definition: Stress - Fluid Mechanics for Mechanical Engineering
| 1. What is stress? |  |
| 2. What is a fluid? |  |
| 3. What is the concept of continuum? |  |
| 4. What are some properties of fluids? |  |
| 5. What is the no-slip condition of viscous fluids? |  |
















