Detailed Notes: Averages | Quantitative for GMAT PDF Download
| Table of contents |

|
| Introduction |

|
| What is an Average? |

|
| Weighted Mean |

|
| Average Speed |

|
| Solved Examples |

|
Introduction
This chapter forms the backbone concept of most questions in the Quantitative Aptitude & Data Interpretation sections. This is a crucial chapter & quick-solving methods in this concept will help you save time - which is an essential factor for your success.
What is an Average?
- Average (or Mean) is defined as the ratio of the sum of the quantities to the number of quantities.
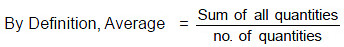
- Following are some examples on average.
Example 1: Find the average of the first five natural numbers.
Sol:First five natural numbers:1, 2, 3, 4, 5
Step 1: Calculate the sum
Sum = 1 + 2 + 3 + 4 + 5
Sum = 1 + 2 + 3 + 4 + 5= 15
Step 2: Count the total number of values
Total numbers = 5
Step 3: Calculate the average
Average = 155 = 3
Therefore, The average of the first five natural numbers is 3.
Example 2: If a person with age 45 joins a group of 5 persons with an average age of 39 years. What will be the new average age of the group?
Sol: Total age will be 45 + 5× 39 = 240. And there will be 6 persons now.
So, the average will be 240/6 = 40.
(or)
Since, 45 is 6 more than 39, by joining the new person, the total will increase by 6 and so the average will increase by 1.
So, the average is 39 + 1 = 40.
Example 3:Two students with marks 50 and 54 leave class VIII A and move to class VIII B. As a result, the average marks of class VIII A fall from 48 to 46. How many students were there initially in class VIII A?
Sol: The average of all the students of class VIII A is 46, excluding these two students.
They have 4 and 8 marks more than 46. So, with the addition of these two students, 12 marks are adding more, and hence the average is increasing 2.
There should be 6 students in that class, including these two. This is the initial number of students.
Weighted Mean
- Let N1, N2, N3, …. Nn be the weights attached to variable values X1, X2, X3, …….. Xn respectively. Then the weighted arithmetic mean, usually denoted by:
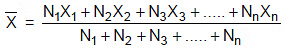
- For any two different quantities taken in different ratios. The weighted average is just like a see-saw.
The more the ratio of a quantity, the more will be the inclination of the average from mid-value towards the value with more ratios.
Example: The average marks of 30 students in a section of class X are 20 while that of 20 students of the second section is 30. Find the average marks for the entire class X.
Sol: Given:
- Section A: Number of students = 30, Average marks = 20
- Section B: Number of students = 20, Average marks = 30
Step 1: Calculate Total Marks for Each Section
Total marks for Section A:
Total MarksA = 301 × 20 = 600
Total marks for Section B:
Total MarksB = 201 × 30 = 600
Step 2: Calculate Total Marks for the Entire Class
Total Marksclass = Total MarksA + Total MarksB = 600 + 600 = 1200
Step 3: Calculate Total Number of Students
Total Students = 30 + 20 = 50
Step 4: Calculate the Average Marks for the Entire Class
Average Marksclass = 120050 = 24
Therefore , average marks of the entire class is 24.
Average Speed
- It is the total distance traveled divided by the time it takes to travel the distance.
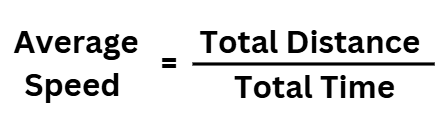 If d1 & d2 are the distances covered at speeds v1 & v2 respectively and the time taken are t1 & t2 respectively, then the average speed over the entire distance (x1 + x2) is given by:
If d1 & d2 are the distances covered at speeds v1 & v2 respectively and the time taken are t1 & t2 respectively, then the average speed over the entire distance (x1 + x2) is given by: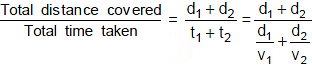
- If both the distances are equal i.e. d1 = d2 = d then,
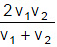 (i.e. Harmonic mean of two velocities)
(i.e. Harmonic mean of two velocities) - But if both the time taken are equal i.e. t1 = t2 = t then,
Average speed.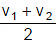 (i.e. Algebraic mean of two velocities)
(i.e. Algebraic mean of two velocities)
Example:The average of 10 consecutive numbers starting from 21 is:
Sol: The average is simply the middle number, which is the average of 5th & 6th no. i.e, 25 & 26 i.e. 25.5
Did You Know?Fact 1:If each number is increased/decreased by a certain quantity n, then the mean also increases or decreases by the same quantity.
Fact 2:If each number is multiplied/ divided by a certain quantity n, then the mean also gets multiplied or divided by the same quantity.
Fact 3: If the same value is added to half of the quantities and the same value is subtracted from the other half quantities, then there will not be any change in the final value of the average.
Solved Examples
Example 1: A man travels 120 km at 60 km per hour and returns the same distance at 40 km per hour. What is his average speed for the entire journey?
Sol: The formula for average speed in a round trip is:
2 × Speed1 × Speed2Speed1 + Speed2
Here, Speed1 = 60 km per hour and Speed2 = 40 km per hour.
Using the formula:
2 × 60 × 4060 + 40 = 4800100 = 48 km per hour
Therefore , the answer to this question is 48 km per hour
Example 2: A grocer mixes two types of sugar. Type A costs ₹30 per kg, and Type B costs ₹50 per kg. How many kilograms of Type B sugar must he mix with 10 kg of Type A to get a mixture worth ₹40 per kg?
Sol:Let x be the quantity of Type B sugar in kg.
Using the weighted average formula:
30 × 10 + 50 × x10 + x = 40
Now, simplify the equation:
300 + 50x = 40 × (10 + x)
300 + 50x = 400 + 40x
Rearrange terms:
50x – 40x = 400 – 300
10x = 100
x = 10
Example 3: A company has three departments:
- Department A has 10 employees with an average salary of ₹60,000.
- Department B has 15 employees with an average salary of ₹80,000.
- Department C has 5 employees with an average salary of ₹50,000.
What is the overall average salary of all employees in the company?
Sol:First, calculate the total salary for each department:
Department A: 10 × 60,000 = 600,000
Department B: 15 × 80,000 = 1,200,000
Department C: 5 × 50,000 = 250,000
Now, sum all the salaries and divide by the total number of employees:
600,000 + 1,200,000 + 250,00010 + 15 + 5 = 2,050,00030 = 68,333.33
Answer: ₹68,333.33
Example 4: A jar contains 10 liters of a solution with 30% salt. Two liters are removed and replaced with pure water. What is the new concentration of salt?
Sol:
Step 1:Initial amount of salt in the solution = 30 × 10100 = 3 liters of salt
Step 2: Salt removed = 30 × 2100 = 0.6 liters of salt
Step 3:Remaining salt after removal: 3 − 0.6 = 2.4 liters.
The total volume of the solution is still 10 liters after replacing the removed 2 liters with pure water.
Step 4:New concentration of salt = 2.410 = 0.24 or 24%
Example 5: The average marks of 3 classes are as follows:
- Class A: 50 students with an average of 75.
- Class B: 30 students with an average of 80.
- Class C: 20 students with an average of 85.
What is the overall average of all the students?
Sol:First, calculate the total marks for each class:
Class A: 50 × 75 = 3,750
Class B: 30 × 80 = 2,400
Class C: 20 × 85 = 1,700Now, sum the total marks and the total number of students:
Total marks:
3,750 + 2,400 + 1,700 = 7,850
Total number of students:
50 + 30 + 20 = 100
The overall average is:
7,850100 = 78.5
|
121 videos|148 docs|111 tests
|
FAQs on Detailed Notes: Averages - Quantitative for GMAT
| 1. What is the difference between average and weighted mean? |  |
| 2. How do you calculate average speed? |  |
| 3. What are some real-life examples of averages? |  |
| 4. Why is the average important in statistics? |  |
| 5. Can the average be misleading? If so, how? |  |















