Distance Between Two Points | Additional Topics for IIT JAM Mathematics PDF Download
Distance Between Two Points
2D distance is the distance between 2 points in a 2D space. In a 2D space, each point, or location in the space, is qualified by 2 parameters like an x-coordinate, and a y-coordinate. We denote the combination of x-coordinate and y-coordinate in something known as an ordered pair, denoted by (x, y). Therefore, the coordinates of some point P would be represented as P(x,y).
The 2D distance between two points is measured by the distance formula. Consider points P1 and P2, with coordinates given as P1(x1, y1) and P2(x2,y2). Therefore, the distance between them would be denoted by d, where:
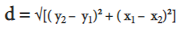
The way to think about distance calculation is in 3 parts:
- Calculate the difference in y-coordinates, and square the difference, denote as quantity q1
- Calculate the difference in x-coordinates, and square the difference, denote as quantity q2
- Take the square root of ( q1 + q2 ).
Example 1
Calculate the distance between the points P1(1,2) and P2(4,3)
Solution: In the given problem, we have: x1 = 1, y1 = 2, x2 = 4, and y2 = 3. Therefore, we have:
q1 = (3-2)² = 1
q2= (4-1)² = 9
distance (d) = √(q1 + q2)
∴ d = √(1 + 9) = √10 = 3.16227 units.
As you can see in the previous example, we have written the units of distance as ‘units’, and not ‘square units.’
Example 2
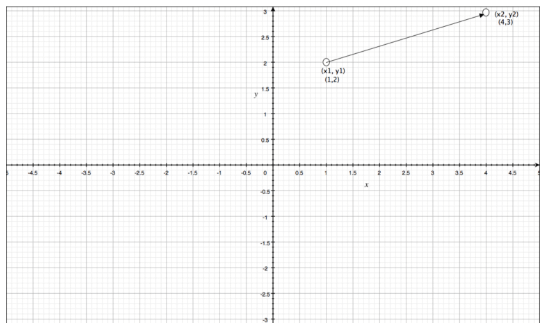
Calculate the distance between the points P1(1,2) and P2(4,2)
Solution: In the given problem, we have: x1 = 1, y1 = 2, x2 = 4, and y2 = 2. Therefore, we have:
q1 = (2-2)² = 0
q2 = (4-1)² = 9
distance (d) = √(q1+q2)
∴ d = √(0 + 9) = √9 = 3 units.
Important Points:
As you can see, in the above problem, we have y2-y1 = 0. This means that the points are on the same horizontal line.
The distance between any two points on the same horizontal line (where y1 = y2) is given by d = |x2 – x1| where | | is used to denote the absolute value of x2 – x1.
Example 3
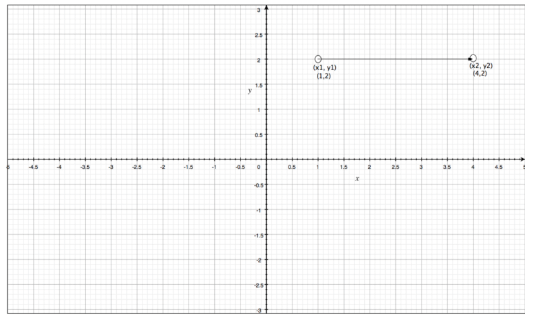
Calculate the distance between the points P1(1,2) and P2(1,5)
Solution: In the given problem, we have: x1 = 1, y1 = 1, x2 = 1, and y2 = 2. Therefore, we have:
q1 = (4-1)²= 9
q2 = (1-1)² = 0
distance (d) = √(q1 + q2)
∴d = √(9 + 0) = √9 = 3 units.
Important Points:
As you can see, in the above problem, we have x1 – x2 = 0. This means that the points are on the same vertical line.
The distance between any two points on the same vertical line (where x1 = x2) is given by d = | y2 – y1 | where | | is used to denote the absolute value of y2 – y1
Solved Question for You
Question: Can the distance between any two points be negative?
Answer: No, the distance between 2 points cannot be negative. This can be thought of in terms of 3 reasons:
- Distance is used to denote a physical quantity, expressing how far two points are from each other, and such a quantity cannot be negative.
- Distance is equal to the square root of the sum of two positive numbers. The sum of two positive numbers is always positive, and the square root of a positive number is always positive.
- In the exceptional case that the distance between 2 points is zero, it is still a non-negative value, hence the distance cannot be negative.
|
2 videos|44 docs|4 tests
|
FAQs on Distance Between Two Points - Additional Topics for IIT JAM Mathematics
| 1. What is the formula to calculate the distance between two points in mathematics? |  |
| 2. How can I find the distance between two points on a graph? |  |
| 3. Is the distance between two points always positive? |  |
| 4. Can the distance between two points be zero? |  |
| 5. How do you interpret the distance between two points in mathematics? |  |






















