Solved Examples for Divisibility | Quantitative for GMAT PDF Download
| Table of contents |

|
| Section - 1 |

|
| Section - 2 |

|
| Section - 3 |

|
| Section - 4 |

|
| Section - 5 |

|
| Section - 6 |

|
| Section - 7 |

|
| Section - 8 |

|
| Section - 9 |

|
| Section - 10 |

|
Section - 1
Ques 1. Is 4,005 divisible by 5?
Ans: Yes: 4,005 ends in 5, so it is divisible by 5.
Ques 2. Does 51 have any factors besides 1 and itself?
Ans: Yes: The digits of 51 add up to a multiple of 3 (5 + 1 = 6), so 3 is a factor of 51.
Ques 3. x = 20
The prime factors of x are:
The factors of x are:
Ans: Prime factors: 2, 2, 5.
Factors: 1, 2, 4, 5, 10, 20
The prime factors of x are: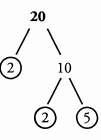
The factors of x are:
Ques 4. If 33 is a factor of 594, is 11 a factor of 594?
Ans: Yes: We could divide 594 by 11 to determine divisibility, but it is faster to use the Factor Foundation rule. The Factor Foundation rule states that if 594 is divisible by 33, 594 will also be divisible by all of the factors of 33. 11 is a factor of 33 (33 = 11 x 3); therefore, 594 is also divisible by 11.
Ques 5. Will 15 divide 4,725?
Ans: Yes: In order to be divisible by 15, a number must be divisible by both 3 and 5, the prime factors that make up 15. Based on the rules of divisibility, because 4,725 ends in a 5, it is divisible by 5. The digits of 4,725 add to 18 (4 + 7 + 2 + 5 = 18), and 18 is divisible by 3— so 4,725 is divisible by 3. Because 4,725 is divisible by 3 and 5, it is also divisible by 15.
Section - 2
Ques 6. Is 123 divisible by 3?
Ans: Yes: The digits of 123 add up to a multiple of 3 (1 + 2 + 3 = 6), so 123 is divisible by 3.
Ques 7. Does 23 have any factors besides 1 and itself?
Ans: No: 23 is a prime number. It has no factors besides 1 and itself.
Ques 8 .x = 100 The prime factors of x are:
The factors of x are:
Ans: Prime factors: 2, 2, 5, 5
Factors: 1 ,2 ,4, 5 ,1 0 ,20 , 25, 50,100
The prime factors of x are: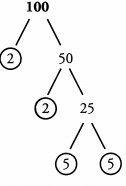
The factors of x are:
Ques 9. If 2,499 is divisible by 147, is 2,499 divisible by 49?
Ans: Yes: The Factor Foundation rule is helpful in this question. The problem states that 2,499 is divisible by 147. The Factor Foundation rule states that if 2,499 is divisible by 147, 2,499 will also be divisible by all of the factors of 147. 147 is divisible by 49 (147/49 = 3). Since 49 is a factor of 147, 2,499 is also divisible by 49.
Ques 10. Name three positive multiples of 12 that are less than 50.
Ans: 12, 24, 36, and 48: In order to generate multiples of 12 that are less than 50, we can multiply 12 by small integers.
12 x 1 = 12
12 x 2 = 24
1 2 x 3 = 36
12 x 4 = 48
All other positive multiples of 12 are larger than 50.
Section - 3
Ques 11. Is 285,284,901 divisible by 10?
Ans: No: 285,284,901 ends in a 1, not a 0. It is not divisible by 10.
Ques 12. Is 539,105 prime?
Ans: No: 539,105 ends in a 5, so 5 is a factor of 539,105. So are 1 and 539,105. Prime numbers have only two factors, so 539,105 is not prime.
Ques 13. x = 42 The prime factors of x are:
The factors of x are:
Ans: Prime factors: 2, 3, 7
Factors: 1, 2, 3, 6 ,7 ,14 ,21 ,42
The prime factors of x are: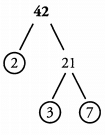
The factors of x are: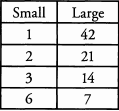
Ques 14. Find four even divisors of 84.
Ans: 2, 4, 6, 12, 14, 28, 42, and 84: The first step in identifying the divisors, or factors, is breaking 84 down into its prime factors. The prime factors of 84 are 2, 2, 3, and 7. In other words, 2 x 2 x 3 x 7 =84. The prime factors can be used to build all of the factors of 84. Because the question asks for even factors, only factors that are built with at least one 2 will be correct.
Even divisors can be built using one 2.
2; 2 x 3 = 6; 2 x 7 = 14; 2 x 3 x 7 = 42
Even divisors can also be built using both the twos that are prime factors of 84.
2 x 2 = 4; 2 x 2 x 3 = 12; 2 x 2 x 7 = 28; 2 x 2 x 3 x 7 = 84
The even divisors of 84 are 2, 4, 6, 12, 14, 28, 42, and 84.
Alternatively, you could make a factor pair table to see which factors are even: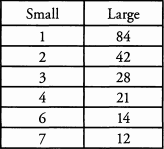
Ques 15. What are the prime factors of 30 x 49?
Ans: 2, 3, 5, 7, and 7: While we could multiply the numbers together to find the prime factors, there is a faster way. The prime factors of the product of 30 and 49 will consist of the prime factors of 30 and the prime factors of 49. The prime factors of 30 are 2, 3, and 5. The prime factors of 49 are 7 and 7. Therefore, the prime factors of 30 x 49 are 2, 3, 5, 7, and 7.
Section - 4
Ques 16: Is 9,108 divisible by 9 and/or by 2?
Ans: 9,108 is divisible by 9 AND by 2: The digits of 9,108 add up to a multiple of 9 (9+1+0 + 8 = 18), so it is a multiple of 9. 9,108 ends in 8, so it is even, which means it is divisible by 2.
Ques 17: Is 937,184 prime?
Ans: No: 937,184 ends in 4, which means its even. Therefore, its divisible by 2. Its also divisible by 1 and itself. Prime numbers have only two factors, so 937,184 is not prime.
Ques 18: x = 39 The prime factors of x are:
The factors of x are:
Ans: Primer factors: 3, 13
Factors: 1, 3, 13, 39
The prime factors of x are: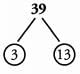
The factors of x are: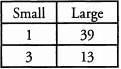
19. How many more prime factors does the product of 28 x 75 have than the product of 14 x 25?
Ans: Two: We could multiply these products out or identify all of the prime factors of each number, but there is a more efficient way. Because the question is asking us to make a comparison, we can just focus on the differences between the two products we are comparing.
28 = 14 x 2 (that is, 28 contains everything that 14 contains, and 28 also has one additional factor of 2)
75 = 25 x 3 (that is, 75 contains everything that 25 contains, and 75 also has one additional factor of 3)
Therefore, the only additional prime factors in 28 x 75 are the 2 in 28 and the 3 in 75. Thus, the first product has two more prime factors than the second product.
Section - 5
Ques 20: Is 43,360 divisible by 5 and/or by 3?
Ans: 43,360 is divisible by 5 but is NOT divisible by 3: 43,360 ends in 0, so it is divisible by 5. The digits of 43,360 do not add up to a multiple of 3 (4 + 3 + 3 + 6 + 0 = 16) so it is not divisible by 3.
Ques 21: Is 81,063 prime?
Ans: No: The digits of 81,063 add up to a multiple of3(8 + l + 0 + 6 + 3 = 18), so 3 is a factor of 81,063. 1 and 81,063 are also factors of 81,063. Prime numbers have only two factors, so 81,063 is not prime.
Ques 22: x = 37 The prime factors of x are:
The factors of x are:
Ans: Prime factors: 37
Factors: 1,37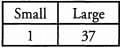
Ques 23: What are the two largest odd factors of 90?
Ans: 45, 15: We can break 90 down into its factor pairs.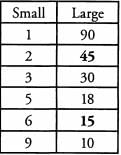
Looking at the table, we can see that 45 and 15 are the two largest odd factors of 90.
Section - 6
Ques 24:Determine which of the following numbers are prime numbers. Remember, you only need to find one factor other than the number itself to prove that the number is not prime.
2 3 5 6
7 9 10 15
17 21 27 29
31 33 258 303
655 786 1,023 1,325
Ans: Not prime: All of the even numbers other than 2 (6, 10, 258, 786), since they are divisible by 2.
All of the remaining multiples of 5 (15, 655, 1,325)
All of the remaining numbers whose digits add up to a multiple of 3, since they are divisible by 3, by definition: 9, 21 (digits add to 3), 27 (digits add to 9), 33 (digits add to 6), 303 (digits add to 6), and 1,023 (digits add to 6). All of these numbers are divisible by 3.
Section - 7
Ques 25: If x is divisible by 33, what other numbers is x divisible by?
Ans: 1, 3, 11, 33: If x is divisible by 33, then x is also divisible by everything 33 is divisible by. The factors of 33 are:
Ques 26: The prime factorization of a number is 3 x 3 x 7. What is the number and what are all its factors?
Ans: 63: The factors are 1, 3 ,7 , 9, 21, and 63. 3 x 3 x 7 = 63
Ques 27: If x is divisible by 8 and by 3, is x also divisible by 12?
Ans: Yes: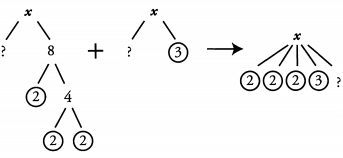
For x to be divisible by 12, we need to know that it contains all of the prime factors of 12. 12 = 2 x 2 x 3. Therefore 12 contains two 2s and a 3. x also contains two 2s and a 3, therefore xis divisible by 12.
Ques 28: If 7x is a multiple of 210, must x be a multiple of 12?
Ans: No: For x to be a multiple of 12, it would need to contain all of the prime factors of 12: 2, 2, and 3. If lx is a multiple of 210, it contains the prime factors 2, 3, 5, and 7. However, we want to know about x, not lx , so we need to divide out the 7. Therefore, x must contain the remaining primes: 2, 3, and 5. Comparing this to the prime factorization of 12, we see that x does have a 2 and a 3, but we don’t know whether it has two 2’s. Therefore, we can’t say that x must be a multiple of 12; it could be, but it doesn’t have to be.
Alternatively, we could start by dividing out the 7. If lx is divisible by 210, x is divisible by 30. We therefore know that x contains the prime factors 2, 3, and 5, and we can follow the remaining reasoning from above.
Ques 29: If integer a is not a multiple of 30, but ab is, what is the smallest possible value of integer 6?
Ans: b = 2: For integer a to be a multiple of 30, it would need to contain all of the prime factors of 30: 2, 3, and 5. Since a is not a multiple of 30, it must be missing at least one of these prime factors. So if ab is a multiple of 30, b must supply that missing prime factor. The smallest possible missing prime is 2. If b - 2 and a = 15 (or any multiple of 15), both of the initial constraints are met.
Section - 8
Ques 30: If 40 is a factor of x, what other numbers are factors of x?
Ans: 1 ,2 ,4 , 5, 8 ,1 0 ,2 0 , and 40: If 40 is a factor of x, then any factor of 40 is also a factor of x.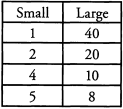
Ques 31: The only prime factors of a number are 5 and 17. What is the number and what are all its factors?
Ans: The number is 85 and the factors are 1, 5, 17, and 85. If 5 and 17 are the only prime factors of the number, then the number = 5 x 17, which means the number is 85.
Ques 32: 5 and 6 are factors of x. Is x divisible by 15?
Ans: Yes: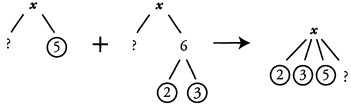
For x to be divisible by 15, we need to know that it contains all of the prime factors of 15. 15 = 3 x 5. Therefore 15 contains a 3 and a 5. x also contains a 3 and a 5, therefore x is divisible by 15.
Ques 33: If q is divisible by 2,6 ,9 ,1 2 ,1 5 , & 30, is q divisible by 8?
Ans: Maybe: To be divisible by 8, q needs three 2s in its prime factorization. Rather than combine all of the listed factors (too hard!), we can just look through and see how many 2s we have.
We cant simply count all of the numbers that contain 2, because we might have some overlapping factors. For instance, 6 is a multiple of 2 and 3, so the fact that q is divisible by both 2 and 6 tells us only that we have at least one 2 (and at least one 3); we don’t necessarily have two factors of 2. Instead, we need to look for the largest number of 2’s we see in one factor. 12 contains two 2’s, so we know that q must be a multiple of 4, but we do not know whether q contains three 2’s. It might or it might not.
Alternately, we could run through our list of factors, adding to the list when new factors appear.
2: q must be divisible by 2.
6: The 3 is new. q must be divisible by 2 and 3.
9: The second 3 is new. q must be divisible by 2, 3, and 3.
12: The second 2 is new. q must be divisible by 2, 2, 3, and 3.
15: The 5 is new. q must be divisible by 2, 2, 3, 3, and 5.
30: Nothing new. q must be divisible by 2, 2, 3, 3, and 5.
Again, we see that we only have two 2s for certain. Therefore q must be a multiple of 180 (that is, 2 x 2 x 3 x 3 x 5), but it does not absolutely have to be a multiple of 8.
Ques 34: If p is a prime number, and q is a non-prime integer, what are the minimum and maximum numbers of factors they can have in common?
Ans: minimum = 1; maximum = 2s Let s start with our more constrained variable: p. Because it is prime, we know that it has exactly 2 factors— itself and 1. Therefore, our maximum number of “factors in common” cannot be more than 2. Can p and q have exactly 2 factors in common? Certainly; q can be a multiple of p. (For instance, i(p = 3 and q = 12, the common factors are 1 and 3.)
What about the minimum? Can p and q have absolutely no factors in common? Try some numbers. If we choose p = 3 and q = 10, then the two numbers don’t have any prime factors in common, but notice that they are both divisible by 1. Any number is always divisible by 1. Therefore, our minimum possible number of factors is 1 (the number one itself) and our maximum is 2 (the two factors of prime number p>.
Section - 9
Ques 35: If 64 divides n, what other divisors does n have?
Ans: If 64 divides n, then any divisors of 64 will also be divisors of n.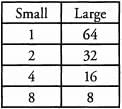
Ques 36: The prime factorization of a number is 2 x 2 x 3 x 11. What is the number and what are all its factors?
Ans: 2 x 2 x 3 x 11 = 132
Ques 37: 14 and 3 divide n. Is 12 a factor of n?
Ans:
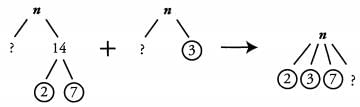
For 12 to be a factor of n, « must contain all of the prime factors of 12. 12 = 2 x 2 x 3, so 12 contains two 2s and a 3. n also contains a 3 but only contains one 2 that we know of, so we don’t know whether 12 is a factor of n.
Ques 38: Positive integers a and b both have exactly four factors. If a is a one-digit number and b = a + 9, a =
Ans: We have a bit of a puzzle here. What kind of number has exactly four factors? Let’s start by looking at our most constrained variable— a. It is a positive one-digit number, so something between 1 and 9, inclusive, and it has four factors. We know that prime numbers have exactly two factors: themselves and one, so we only need to look at non-prime one-digit positive integers. That’s a small enough field that we can list them out:
1—just one factor!
4— 3 factors: 1, 2, and 4
6— 4 factors: 1, 2, 3, and 6
8— 4 factors: 1, 2, 4, and 8
9— 3 factors: 1, 3, and 9
So our two possibilities for a are 6 and 8. We now have to apply our two constraints for b. It is 9 greater than a, and it has exactly four factors. Here are our possibilities:
If a - 6, then b - 15. 15 has 4 factors: 1, 3, 5, and 15.
If a — 8, then b = 17. 17 is prime, so it has only has 2 factors: 1 and 17.
Only b - 15 works, so a must be 6.
Ques 39: If n is the product of 2,3, and a two-digit prime number, how many of its factors are greater than 6?
Ans: Because we have been asked for a concrete answer, we can infer that the answer will be the same regardless of which 2-digit prime we pick. So for simplicity’s sake, let’s pick the smallest and most familiar one: 11.
If n is the product of 2, 3, and 11, its factors are: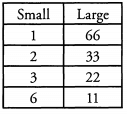
In this case, we can simply use the right-hand portion of our chart. We have four factors larger than 6: 11, 22, 33, and 66.
Notice that because the other given prime factors of n (2 and 3) multiply to get exactly 6, we can only get a number greater than 6 by multiplying by the third factor, the “two-digit prime number.” The right hand column represents that third factor multiplied by all of the other factors: 11 x 6, 11 x 3, 11 x 2, and 11 x 1. If we replace 11 with another two-digit prime, we will get the same result.
Section - 10
Ques 40. If n is a multiple of both 21 and 10, is 30 a divisor of n?
Ans: Yes: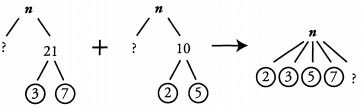
For 30 to be a divisor of n, n has to contain all of the prime factors of 30. 30 = 2 x 3 x 5, so 30 contains 2, 3, and 5. n also contains 2, 3 and 5, so 30 is a divisor of n.
Ques 41: 4,2 1, and 55 are factors of n. Does 154 divide n?
Ans: 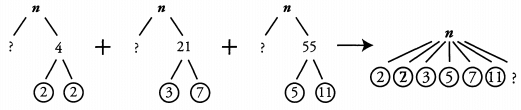
For 154 to divide n, n has to contain all the same prime factors as 154. 154 = 2 x 7 x 11, so 154 contains 2, 7, and 11. n also contains 2, 7 and 11, so 154 divides n.
Ques 42: If n is divisible by 196 and by 15, is 270 a factor of n?
Ans: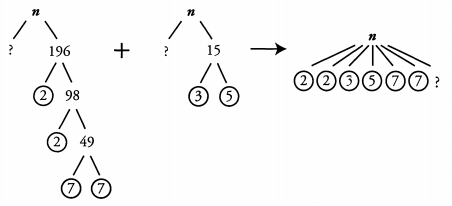
For 270 to be a factor of n, n must contain all the same prime factors as 270. 270 = 2 x 3 x 3 x 3 x 5, so 270 contains a 2, three 3 s, and a 5. n contains a 2 and a 5, but only one 3. Therefore, 270 is not definitely a factor of n.
|
121 videos|148 docs|111 tests
|
FAQs on Solved Examples for Divisibility - Quantitative for GMAT
| 1. What are divisibility rules? |  |
| 2. How can I determine if a number is divisible by 2? |  |
| 3. What is the divisibility rule for 3? |  |
| 4. How can I determine if a number is divisible by 5? |  |
| 5. Are there any divisibility rules for prime numbers? |  |
















