Irodov Solutions: Dynamics of A Solid Body- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 251. A uniform cylinder of radius R and mass M can rotate freely about a stationary horizontal axis O (Fig. 1.59). A thin cord of length l and mass m is wound on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length x of the hanging part of the cord. The wound part of the cord is supposed to have its centre of gravity on the cylinder axis.
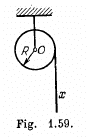
Ans. Let us use the equation  relative to the axis through O (1)
relative to the axis through O (1)
For this purpose, let us find the angular momentum of the system Mz about the given rotation axis and the corresponding torque Nz. The angular momentum is
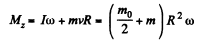
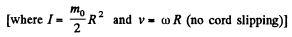
So, 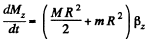 (2)
(2)
The downward pull of gravity on the overhanging part is the only external force, which exerts a torque about the z -axis, passing through O and is given by,
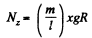
Hence from the equation 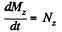
Thus, 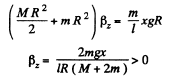
Note : We may solve this problem using conservation of mechanical energy of the system (cylinder + thread) in the uniform field of gravity.
Q. 252. A uniform sphere of mass m and radius R rolls without slipping down an inclined plane set at an angle α to the horizontal. Find:
(a) the magnitudes of the friction coefficient at which slipping is absent;
(b) the kinetic energy of the sphere t seconds after the beginning of motion.
Ans. (a) Let us indicate the forces acting on the sphere and their points of application. Choose positive direction of x and cp (rotation angle) along the incline in downward direction and in the sense of  undirectional rotation) respectively. Now from equations of dynamics o f rigid body i.e.
undirectional rotation) respectively. Now from equations of dynamics o f rigid body i.e. 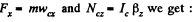
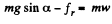 (1)
(1)
and 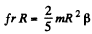 (2)
(2)
But 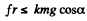 (3)
(3)
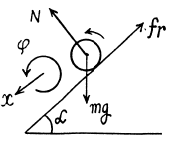
In addition, the absence of slipping provides the kinematical realtionship between the accelerations :
w = βR (4)
The simultaneous solution of all the four equations yields :
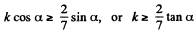
(b) Solving Eqs. (1) and (2) [of part (a)], we :
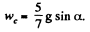
As the sphere starts at t = 0 along positive x axis, for pure rolling
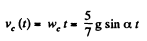 (5)
(5)
Hence the sought kinetic energy
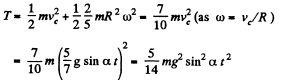
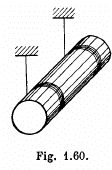
Q. 253. A uniform cylinder of mass m = 8.0 kg and radius R = 1.3 cm (Fig. 1.60) starts descending at a moment t = 0 due to gravity. Neglecting the mass of the thread, find:
(a) the tension of each thread and the angular acceleration of the cylinder;
(b) the time dependence of the instantaneous power developed by the gravitational force.
Ans. (a) Let us indicate the forces and their points of application fox the cylinder. Choosing the positive direction for x and φ as shown in the figure, we write the equation of motion of the cylinder axis and the equation of moments in the C.M. frame relative to that axis i.e. from equation


As there is no slipping of thread on the cylinder
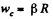
From these three equations
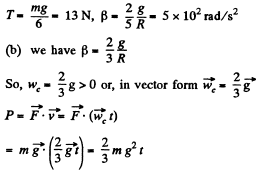
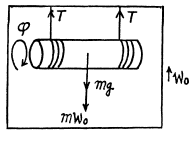
Q. 254. Thin threads are tightly wound on the ends of a uniform solid cylinder of m ass m. The free ends of the threads are attached to the ceiling of an elevator car. The car starts going up with an accelera- tion w0. Find the acceleration w' of the cylinder relative to the car and the force F exerted by the cylinder on the ceiling (through the threads).
Ans. Let us depict the forces and their points of application corresponding to the cylinder attached with the elevator. Newton's second law for solid in vector form in the frame of elevator, gives :
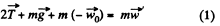
The equation of moment in the C.M. frame relative to the cylinder axis i.e. from
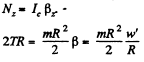
[as thread does not slip on the cylinder, W' = PR ]
or, 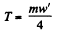
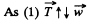
so in vector form
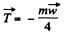 (2)
(2)
Solving Eqs.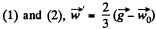
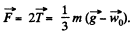
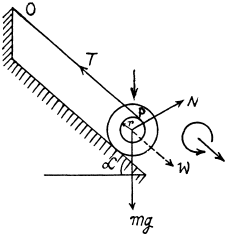
Q. 255. A spool with a thread wound on it is placed on an inclined smooth plane set at an angle α = 30° to the horizontal. The free end of the thread is attached to the wall as shown in Fig. 1.61. The mass of the spool is m = 200 g, its moment of inertia relative to its own axis I = 0.45 g.m2, the radius of the wound thread layer r = 3.0 cm. Find the acceleration of the spool axis.
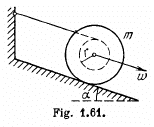
Ans. Let us depict the forces and their points of application for the spool. Choosing the positive direction for x and φ as shown in the fig., we apply F = mw and N* - I. p. and get 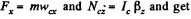
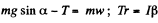
“Notice that if a point of a solid in plane motion is connected with a thread, the projection of velocity vector of the solid’s point of contact along the length of the thread equals the velocity of the other end of the thread (if it is not slacked)”
Thus in our problem, 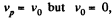 hence point P is the instantaneous centre of rotation of zero velocity for the spool. Therefore vc = ωr and subsequently wc = βr
hence point P is the instantaneous centre of rotation of zero velocity for the spool. Therefore vc = ωr and subsequently wc = βr
Solving the equations simultaneously, we get
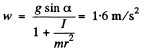
Q. 256. A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F (Fig. 1.62). Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k. What is the ac- celeration wmax of the axis of the cylinder rolling down the inclined plane?
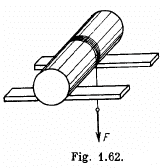
Ans. Let us sketch the force diagram for solid cylinder and apply Newton’s second law in projection form along x and y axes (Fig.) :
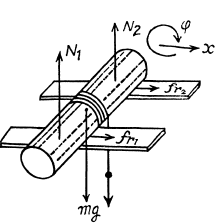
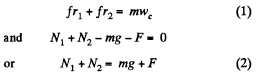
Now choosing positive direction of <p as shown in the figure and using Ncz = Ic βz, 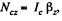
we get
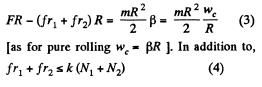
Solving the Eqs., we get

and 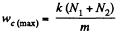
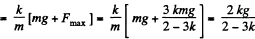
Q. 257. A spool with thread wound on it, of mass m, rests on a rough horizontal surface. Its moment of inertia relative to its own axis is equal to I = γmR2, where γ is a numerical factor, and R is the outside radius of the spool. The radius of the wound thread layer is equal to r. The spool is pulled without sliding by the thread with a constant force F directed at an angle α to the horizontal (Fig. 1.63). Find:
(a) the projection of the acceleration vector of the spool axis on the x-axis;
(b) the work performed by the force F during the first t seconds after the beginning of motion.

Ans. (a) Let us choose the positive direction of the rotation angle φ, such that wcx and βz have identical signs (Fig.). Equation of motion, 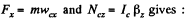
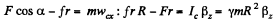
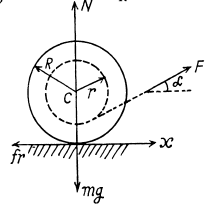
In the absence of the slipping of the spool 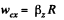
From the three equations 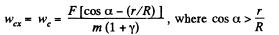 (1)
(1)
(b) As static friction (fr) does not work on the spool, from the equation of the increment of mechanical eneigy Aext = ΔT.
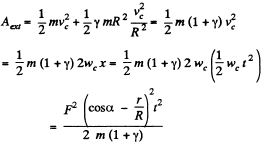
Note\that at cos α = r/R, there is no rolling and for 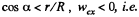 the spool will move towards negative x-axis and rotate in anticlockwise sense.
the spool will move towards negative x-axis and rotate in anticlockwise sense.
Q. 258. The arrangement shown in Fig. 1.64 consists of two identical uniform solid cylinders, each of mass m, on which two light threads are wound symmetrically. Find the tension of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.
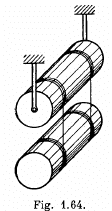
Ans. For the cylinder from the equation  about its stationary axis of rotation.
about its stationary axis of rotation.
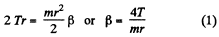
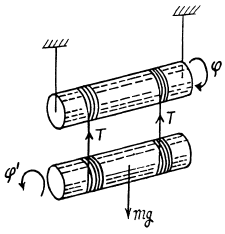
For the rotation of the lower cylinder from the equation 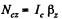
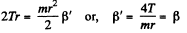
Now for the translational motion of lower cylinder from the 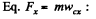
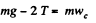 (2)
(2)
As there is no slipping of threads on the cylinders :
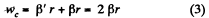
Simultaneous solu tion of (1), (2) and (3) yields
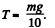
Q. 259. In the arrangement shown in Fig. 1.65 a weight A possesses mass m, a pulley B possesses mass M. Also known are the moment of inertia I of the pulley relative to its axis and the radii of the pulley R and 2R. The mass of the threads is negligible. Find the acceleration of the weight A after the system is set free.

Ans. Let us depict the forces acting on the pulley and weight A, and indicate positive direction for x and φ as shown in the figure. For the cylinder from the equation 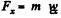 and
and 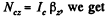
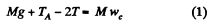
and 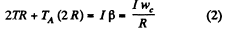
For the weight A from the equation
As there is no slipping of the threads on the pulleys.
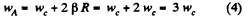
Simultaneous solutions of above four equations gives :
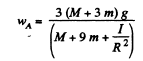
Q. 260. A uniform solid cylinder A of mass m1 can freely rotate about a horizontal axis fixed to a mount B of mass m2 (Fig. 1.66). A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find:
(a) the acceleration of the point K;
(b) the kinetic energy of this system t seconds after the beginning of motion.
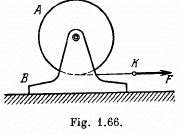
Ans. (a) For the translational motion of the system (m1 + m2), from the equation Fx = mwcx
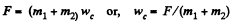 (1)
(1)
Now for the rotational motion of cylinder from the equation : Ncx = Ic βz
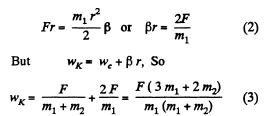
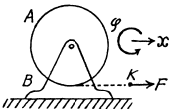
(b) From the equation of increment of m echanical energy : ΔT = Aext
Here 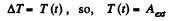
As force F is constant and is directed along jc-axis the sought work done.
Aext = Fx
(where x is the displacement of the point of application of the force F during time interval t)
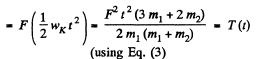
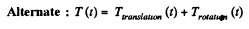
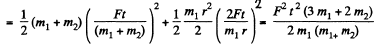
Q. 261. A plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what accelerations will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
Ans. Choosing the positive direction for x and <p as shown in Fig, let us we write the equation of motion for the sphere 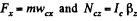
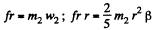
(w2 is the acceleration of the C .M . o f sphere.)
For the plank from the Eq. Fx = mwx F - f r = m1 w1
In addition, the condition for the absence of slipping of the sphere yields the kinem atical relation between the accelerations :
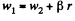

Sim ultaneous solution of the four equations yields :
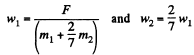
Q. 262. A uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity ω0, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to k.
Find:
(a) how long the cylinder will move with sliding;
(b) the total work performed by the sliding friction force acting on the cylinder
Ans. (a) Let us depict the forces acting on the cylinder and their point of applications for the cylinder and indicate positive direction of x and φ as shown in the figure. From the equations for the plane motion of a solid 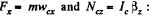
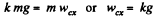 (1)
(1)
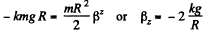 (2)
(2)
Let the cylinder starts pure rolling at t = t0 after releasing on the horizontal floor at t = 0. From the angular kinematical equation
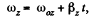
or 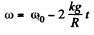 (3)
(3)
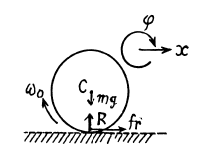
From the equation of the linear kinem atics,
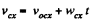
or 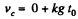
But at the moment t = t0, when pure rolling starts ve = ωR
so, 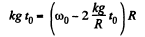
Thus 
(b) As the cylinder pick, up speed till it starts rolling, the point of contact has a purely translatory movement equal to 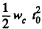 in the forward directions but there is also a backward movement of the point of contact of magnitude
in the forward directions but there is also a backward movement of the point of contact of magnitude 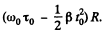 Because of slipping the net displacement is backwards. The total work done is then,
Because of slipping the net displacement is backwards. The total work done is then,
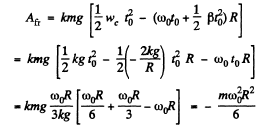
The sam e result can also be obtained by the work-energy theorem, Afr = ΔT.
Q. 263. A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R. Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
Ans. Let us write the equation of motion for the centre of the sphere at the moment of breaking-off:
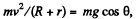
where v is the velocity of the centre of the sphere at that moment, and θ is the corresponding angle (Fig.). The velocity v can be found from the energy conservation law :
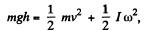
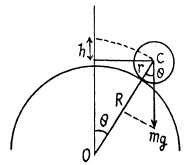
where l is the moment of inertia of the sphere relative to the axis passing through the sphere’s
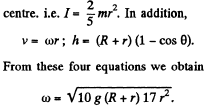
Q. 264. A uniform solid cylinder of radius R = 15 cm rolls over a horizontal plane passing into an inclined plane forming an angle α = 30° with the horizontal (Fig. 1.67). Find the maximum value of the velocity v0 which still permits the cylinder to roll onto the inclined plane section without a jump. The sliding is assumed to be absent.
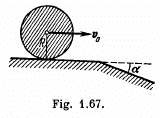
Ans. Since the cylinder moves without sliding, the centre of the cylinder rotates about the point O, while passing through the common edge of the planes. In other words, the point O becomes the foot of the instantaneous axis of rotation of the cylinder.
It at any instant during this motion the velocity of the C.M. is v1 when the angle (shown in the figure) is β, we have

where N is the normal reaction of the edge
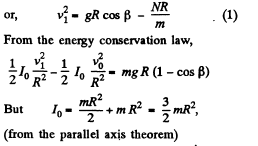
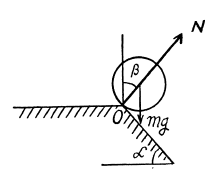
Thus, 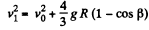
From (1) and (2)
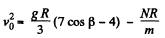
The angle β in this equation is clearly smaller than or equal to α so putting β = α we get
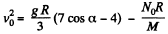
where N0 is the corresponding reaction. Note that N > N0. No jumping occurs during this turning if N0 > 0. Hence, v0 must be less than
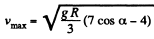
Q. 265. A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane; at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity v0 (Fig. 1.68). At what values of v0 will the hoop move without bouncing?
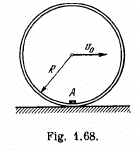
Ans. Clearly the tendency of bouncing of the hoop will be maximum when the small body A, will be at the highest point of the hoop during its rolling motion. Let the velocity of C.M. of the hoop equal v at this position. The static friction does no work on the hoop, so from conservation of mechanical energy; E1 = E2

or 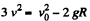 (1)
(1)
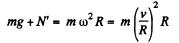 (2)
(2)
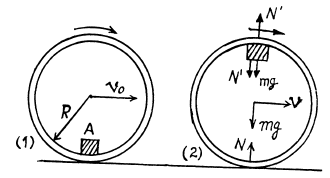
As the hoop has no acceleration in vertical direction, so for the hoop,
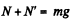 (3)
(3)
From Eqs. (2) and (3),
 (4)
(4)
A s the hoop does not bounce, N > 0 (5)
So from Eqs. (1), (4) and (5),
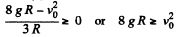
Hence 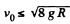
FAQs on Irodov Solutions: Dynamics of A Solid Body- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are the basic principles of dynamics in a solid body? |  |
| 2. How can I solve problems related to dynamics of a solid body in the NEET exam? |  |
| 3. What are the common types of motion observed in solid bodies? |  |
| 4. How does the distribution of mass affect the dynamics of a solid body? |  |
| 5. Can you provide an example of a real-world application of dynamics in a solid body? |  |

















