Creep, Elastic Strain | Strength of Materials (SOM) - Mechanical Engineering PDF Download
| Table of contents |

|
| Creep |

|
| Tension Test |

|
| Elastic strain and Plastic strain |

|
| Elasticity |

|
| Plasticity |

|
| Strain hardening |

|
Creep
When a member is subjected to a constant load over a long period, it undergoes a slow permanent deformation, and this is termed “creep”. This is dependent on temperature. Usually, at elevated temperatures, creep is high.
- The materials have their different melting point; each will creep when the homologous temperature > 0.5.
Homologous temp = Testing temperature / Melting temperature > 0.5
A typical creep curve shows three distinct stages with different creep rates. After an initial rapid elongation εο, the creep rate decreases with time until reaching the steady state.
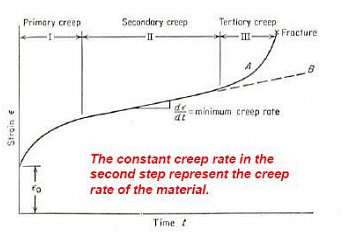 creep curve
creep curve
- Primary creep is a period of transient creep. The creep resistance of the material increases due to material deformation.
- Secondary creep provides a nearly constant creep rate. The average value of the creep rate during this period is called the minimum creep rate. A stage of balance between competing. Strain hardening and recovery (softening) of the material.
- Tertiary creep shows a rapid increase in the creep rate due to an effectively reduced cross-sectional area of the specimen, leading to creep rupture or failure. In this stage, intergranular cracking and/or formation of voids and cavities occur.
Creep rate = c1 σc2
Creep strain at any time = zero time strain intercept + creep rate ×Time
= εo + c1 σc2 ∗ t
Where, c1, c2 are constants σ = stress
- If a load P is applied suddenly to a bar, then the stress & strain induced will be double than those obtained by an equal load applied gradually.
- Stress produced by a load P in falling from a height 'h'
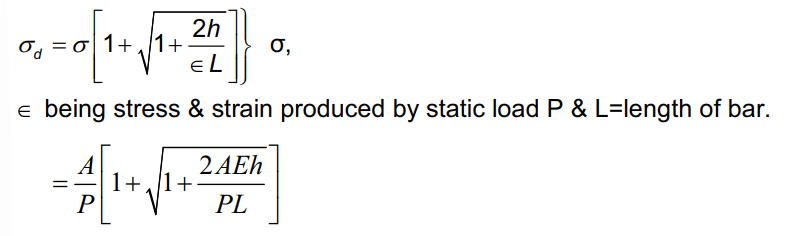 I
I
- Loads shared by the materials of a compound bar made of bars x & y due to load W,
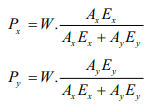 Formula
Formula
- Elongation of a compound bar
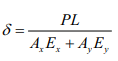 Elongation
Elongation
Tension Test
 Graphical representation
Graphical representation
- True elastic limit: based on micro-strain measurement at strains on the order of 2 ×10-6. Very low value and is related to the motion of a few hundred dislocations.
- Proportional limit: the highest stress at which stress is directly proportional to strain.
- Elastic limit: is the greatest stress the material can withstand without any measurable permanent strain after unloading. Elastic limit > proportional limit.
- Yield strength is the stress required to produce a small specific amount of deformation. The offset yield strength can be determined by the stress corresponding to the intersection of the stress-strain curve and a line parallel to the elastic line offset by a strain of 0.2 or 0.1% (ε = 0.002 or 0.001).
- The offset yield stress is referred to as proof stress, either at 0.1 or 0.5% strain, used for design and specification purposes to avoid the practical difficulties of measuring the elastic limit or proportional limit
- Tensile strength or ultimate tensile strength (UTS) σu is the maximum load Pmax divided by the original cross-sectional area Ao of the specimen.
- % Elongation, = Lf - Lo / Lo, is chiefly influenced by uniform elongation, which is dependent on the strain-hardening capacity of the material.
- Reduction of Area: q = Ao - Af / Ao
- Reduction of area is more a measure of the deformation required to produce failure, and its chief contribution results from the necking process.
- Because of the complicated state of stress in the neck, values of reduction of area are dependent on specimen geometry, deformation behaviour, and they should not be taken as true material properties.
- RA is the most structure-sensitive ductility parameter and is useful in detecting quality changes in the materials.
- Stress-strain response
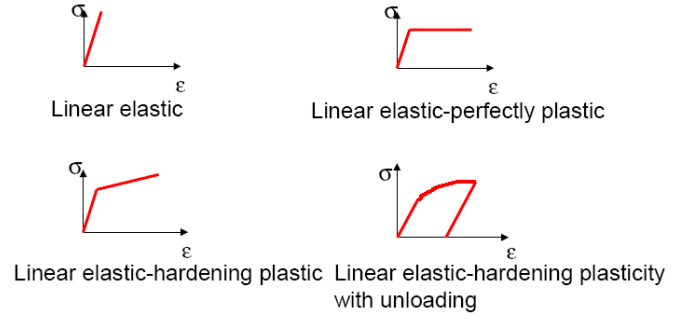 Stress-strain response
Stress-strain response
Elastic strain and Plastic strain
The strain present in the material after unloading is called the residual strain or plastic strain, and the strain that disappears during unloading is termed as recoverable or elastic strain. The equation of the straight line CB is given by
σ = εtotal * E - εplastic * E = εplastic * E
Carefully observe the following figures and understand which one is Elastic strain and which one is Plastic strain.
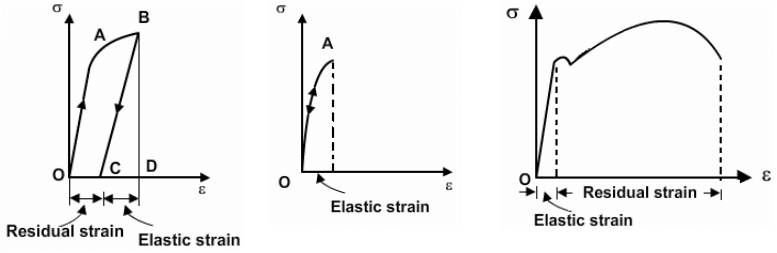 Graphical representation
Graphical representation
Elasticity
- This is the property of a material to regain its original shape after deformation when the external forces are removed.
- When the material is in the elastic region, the strain disappears completely after the removal of the load.
- The stress-strain relationship in the elastic region need not be linear and can be non-linear (example: rubber).
- The maximum stress value below which the strain is fully recoverable is called the elastic limit.
- It is represented by point A in the figure.
- All materials are elastic to some extent, but the degree varies; for example, both mild steel and rubber are elastic materials, but steel is more elastic than rubber.
 Graph
Graph
Plasticity
- When the stress in the material exceeds the elastic limit, the material enters into the plastic phase where the strain can no longer be completely removed.
- Under plastic conditions, materials ideally deform without any increase in stress.
- A typical stress-strain diagram for an elastic-perfectly plastic material is shown in the figure.
- Mises-Henky criterion gives a good starting point for plasticity analysis.
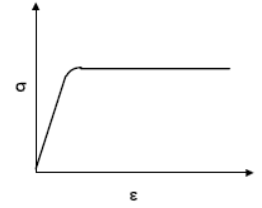 Graph
Graph
Strain hardening
- If the material is reloaded from point C, it will follow the previous unloading path and line CB becomes its new elastic region with elastic limit defined by point B.
- Though the new elastic region CB resembles that of the initial elastic region OA, the internal structure of the material in the new state has changed.
- The change in the microstructure of the material is clear from the fact that the ductility of the material has come down due to strain hardening.
- When the material is reloaded, it follows the same path as that of a virgin material and fails on reaching the ultimate strength which remains unaltered due to the intermediate loading and unloading process.
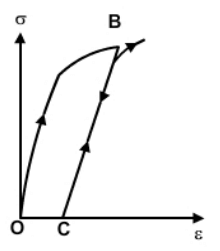 Graph
Graph
Stress reversal and stress-strain hysteresis loop
- We know that fatigue failure begins at a local discontinuity, and when the stress at the discontinuity exceeds the elastic limit, there is plastic strain.
- The cyclic plastic strain results in crack propagation and fracture.
- When we plot the experimental data with reversed loading and the true stress-strain hysteresis loops is found as shown below.
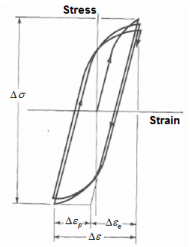 True stress-strain plot with a number of stress reversals
True stress-strain plot with a number of stress reversals
- Due to cyclic strain, the elastic limit increases for annealed steel and decreases for cold-drawn steel.
- Here, the stress range is Δσ.
- Δεp and Δεo are the plastic and elastic strain ranges, the total strain range being Δε.
- Considering that the total strain amplitude can be given as
Δε = Δεp + Δεe
|
37 videos|103 docs|47 tests
|
FAQs on Creep, Elastic Strain - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is creep and how does it relate to mechanical engineering? |  |
| 2. How is tension testing used to determine elastic and plastic strain? |  |
| 3. What is the difference between elasticity and plasticity in mechanical engineering? |  |
| 4. How does strain hardening affect the mechanical properties of a material? |  |
| 5. What are some common elastic constants used in mechanical engineering? |  |




















