Enthalpy, Heat, Internal Energy & Work Done Calculations in Different Processes | Chemistry for JEE Main & Advanced PDF Download
Enthalpy, Heat, Internal Energy & Work Done Calculations in Different Processes
(1) Isochoric process
V = constant 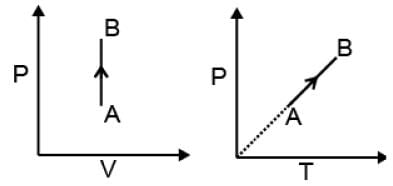
dV = 0
| W = 0 |
dU = dqV
ΔU = qV = nCVΔT
| ΔH = nCpΔT |
Calculation of q, w, ∆H, ∆U for an IRREVERSIBLE ISOCHORIC process involving an ideal gas:
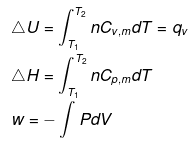
w= 0
∵ dV = 0
(2) Isobaric process
W = - Pext (V2-V1)Reversible & isobaric process
W = - P (V2-V1)
= - nR (T2-T1)
Irreversible & isobaric process
P1 = P2 = Pext
For reversible & irreversible isobaric or isochoric process, workdone is same.
(3) Isothermal process
(a) Reversible Expansion or compressionW = -P∫ dv
= -∫Pgas dV
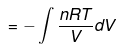
In Expansion W = - ve
ΔE = 0
| q = -W |
Calculation of q, w , ∆H, ∆U for a reversible isothermal process involving an ideal gas :
ΔU = q + w = 0 ⇒ -w
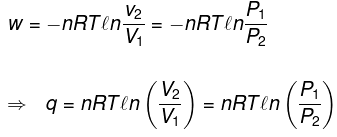
(b) Single stage irreversible expansion
W = - Pext(V2 - V1)
|Wrev| > |Wirr| (in case of expansion)
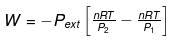
(c) Two Stage irreversible Expansion
Stage I. Pext = 3 atm, Pi = 5 atm
Stage II. Pext = 2 atm , Pf = 2 atm
Work done in 2nd stage > Work done in Ist stage
(d) n- stage expansion
Compression - (One stage Compression )
| Wirr | = Pext DV
P1 = 1 atm , P2 = 5 atm , Pext = 5 atm
| Wirr | > | Wrev | For compression
Calculation of q, w, ∆H, ∆U for an Irreversible isothermal process involving an ideal gas:
For isothermal process involvingΔH = ΔU = 0 ∵ ΔT = 0
Also,
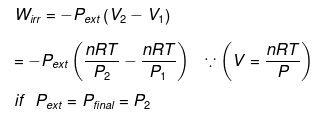
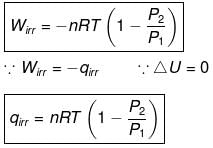
For isobaric process
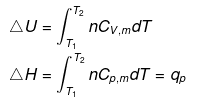
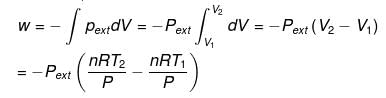
= -nR(T2 - T1) (∵ Pext = P)
= -nRΔT
Example 1. 2 moles of an ideal gas initially present in a piston fitted cylinder at 300 K, and 10 atm are allowed to expand against 1 atm but the piston was stopped before it stablished the mechanical equilibrium. If temperature were maintained constant through out the change and system delivers 748.26 J of work, determine the final gas pressure and describe the process on PV diagram.
Solution.
Wirrv = - 748.26
Wirr = - Pext [1/P2- 1/P1]nRT
P2 = 4atm
Example 2. 1150 Kcal heat is released when following reaction is carried out at constant volume.
C7H16(l) 11O2(g) → 7CO2(g) 8H2O(l)
Find the heat change at constant pressure.
The pressure of liquid is a linear function of volume (P = a + bV) and the internal energy of the liquid is U = 34 + 3PV find a, b, w, ΔE & ΔH for change in state from 100 Pa, 3m3 to 400 Pa, 6m3
Solution. 100 = a + bV
⇒ 100 = a + 3b
Also, 400 = a + 6b
⇒ a = -200, b = 100
ΔU = 34 + 3(P2V2 - P1V1)
= 6300 J
ΔH = ΔU + P2V2 - P1V1
= 6300 + 2100 = 8400 J
P is a linear function
Pext = (400 + 100)/2 = 250
W = - Pext(dV)
= - 250(6 - 3) = - 750 J
Example 3. 4 moles of an ideal gas (Cv = 15 J) is subjected to the following process represented on P - T graph. From the given data find out whether the process is isochoric or not ? also calculate q, w, ΔU, ΔH,
Solution. PV = nRT
4V = 4R × 400
V = 400 R ........(1)
3V = 4R × 300
⇒ V = 400 R ........(2)
i.e., V is constant
w = 0
ΔU = nCV + ΔT ⇒ 4 ×15 ×100 = 6000 J
ΔH = nCP + ΔT ⇒ n (CV + R ) ΔT
⇒ 4 ×(15 8.3)×100
⇒ 9320 J
| q = ΔU = 6kj |
Example 4. 2 mole of a gas at 1 bar and 300 K are compressed at constant temperature by use of a constant pressure of 5 bar. How much work is done on the gas ?
Solution. 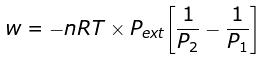 = 19953.6 J
= 19953.6 J
Example 5. 2 moles of an ideal diatomic gas (CV = 5/2 R) at 300 K, 5 atm expanded irreversibly and adiabatically to a final pressure of 2 atm against a constant pressure of 1 atm.
(1) Calculate final temperature q, w, ΔH & ΔU
(2) Calculate corresponding values if the above process is carried out reversibly.
Solution.
w = CV (T2 - T1)
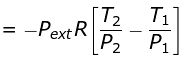
Given T2 = 270K
Pext = 1,P2 = 2,P1 = 5
q = 0
w = ΔU = nCVΔT
= -1247.1 J
ΔH = nCPΔT
= 1745.94 J
If process is reversible Pvγ = Constant
P1- γTγ = Constant
| T = 231 K |
Example 6. 10 gm of Helium at 127°C is expanded isothermally from 100 atm to 1 atm Calculate the work done when the expansion is carried out
(i) In single step
(ii) In three steps the intermediate pressure being 60 and 30 atm respectively and
(iii) Reversibly.
Solution.
(i) Work done = V.ΔP
(ii) In three steps
VI = 83.14 × 10-5 m3
WI = (83.14 × 10-5) × (100 - 60) × 105
= 3325.6 Jules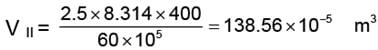
WII = V. DP
WII = 138.56 × 10-5 (60 - 30) × 105
= 4156.99 ≈ 4157 J.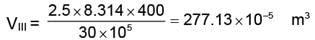
WIII = 277.13 × 10-5 (30 - 1) × 105
WIII = 8036.86 J.
W total = WI + WII + WIII
= 3325.6 + 4156.909 + 8036.86 = 15519.45 J.
(iii) For reversible process
Example 7. Calculate the amount of work done by 2 mole of an ideal gas at 298 K in reversible isothermal expansion from 10 litre to 20 litre.
Solution. Amount of work, done in reversible isothermal expansion,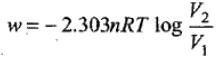
Given, n = 2, R = 8.314 JK-1 mol-1, T = 298 K, V2 = 20 L and V1 = 10 L.
Substituting the values in above equation,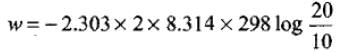
= -2.303 × 8.314 × 298 × 0.3010 = -3434.9 J
i.e., work is done by the system.
Example 8. 5 moles of an ideal gas expand isothermally and reversibly film a pressure of 10 atm to 2atm at 300K. What is the largest mass which can be lifted through a height of l metre in this expansion?
Solution. Work done by the system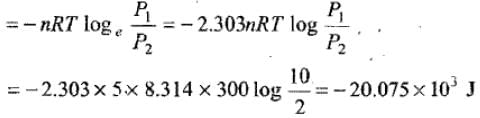
Let M be the mas which can be lifted through a height of 1 m.
Work done in lifting the mass = Mgh = M × 9.8 × 11
So, M × 9.8 = 20.075 × 103 M
= 2048.469 kg
(4) Adiabatic Ideal Gas Expansion & Compression
dq = 0
dU = dW
| Δ U = W |
| W = nCV ΔT = nCV T2 - T1) |
For an ideal gas CP - CV = R
Reversible Adiabatic Ideal Gas Expansion & Compression
nCVdT = - Pext dV
Pint = dP = Pext
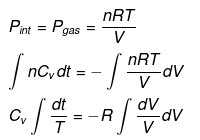
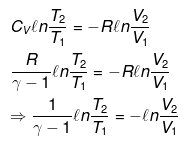
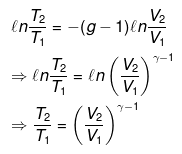
⇒ T2(V2)γ - 1 = V1γ - 1T1
TVγ - 1 = Constant
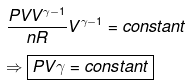
Calculation of q, w, ∆H, ∆U for reversible adiabatic process:
dq = 0 ⇒ dU = dw
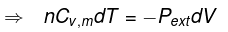
for a reversible change
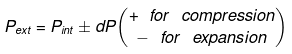
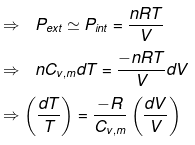
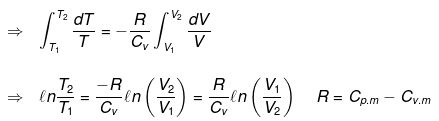
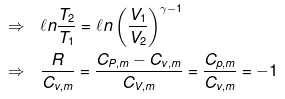
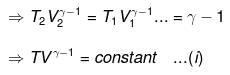
Now substituting V = nRT/P in equation
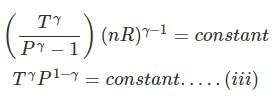
substituting T = PV/nR in eq...
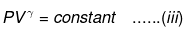
⇒ Equation (i), (ii) and (iii) is valid only for reversible adiabatic process, for irreversible adiabatic process these equations are not applicable.
- Expression for work:
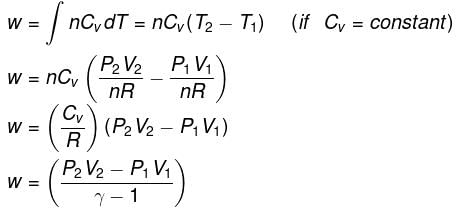
- Expression for ΔH and ΔU
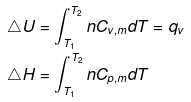
Irreversible Adiabtic Ideal Gas Expansion & Compression
dU = dW
⇒ nCV(T2 - T1) = - Pext dV
= - Pext [V2 - V1]
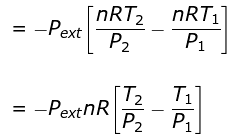
Calculation of Q, W, ∆H, ∆U For Irreversible Adiabatic Process involving An Ideal Gas:
Operation wise adiabatic process and isothermal process are similar hence all the criteria that is used for judging an isothermal irreversible process are applicable to adiabatic process.If large amount of dust particles are removed abruptly an irreversible adiabatic expansion take place.
In an irreversible adiabatic process, an ideal gas is subjected to compression or expansion in a thermally insulated vessel.
The heat absorbed in the process =0
⇒ dU = wirr ....(i)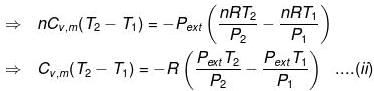
If Pext, = P2 = Pfinal
Then
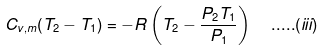
eq. (ii) or (iii) can be solved for T2
Expression for w
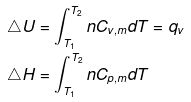
Note: If two states A and B are connected by a reversible path then they can never be connected by an irreversible path.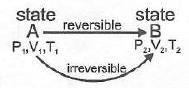 If the two states are linked by an adiabatic reversible and irreversible path then wrev = ∆Urev
If the two states are linked by an adiabatic reversible and irreversible path then wrev = ∆Urev
But as U is a state function
Therefore, ∆U irrev = ∆Urev
wirrev = wrev
as work is a path function.
If we assume that
wirrev = wrev
It implies that which again is a contradiction as U is a state function.
∆U irrev ≠ ∆Urev
Two states A and B can never lie both on a reversible as well as irreversible adiabatic path.
There lies only one unique adiabatic path linkage between two states A and B.
Example 1. Two moles of an ideal monoatomic gas at NTP are compressed adiabatically and reversibly to occupy a volume of 4.48 dm3. Calculate the amount of work done, ∆U, final temperature and pressure of the gas. Cv for ideal gas 12.45J K -1 mol-1.
Solution. For an ideal gas,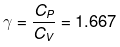
Initial volume, V1 = 2 × 22.4 = 44.8 dm3
Initial pressure, P1 = 1 atm
Initial temperature, T1 = 273 K
Final volume, V2 = 4.48 dm3
Let the final pressure be P2 and temperature be T2
Applying
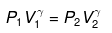
or
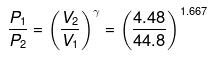
or
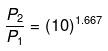
P2 = (10)1.667(P1 = 1 given)
log P2 = 1.667 log 10= 1.667
P2 = antilog 1.667= 46.45 atm
Final temperature
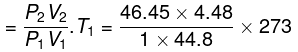
= 1268 K
Work done on the system = n.Cv.ΔT
= 2 × 12.45 × (1268 - 273)
= 2 × 12.45 × 995 = 24775.5 J
From the first law of thermodynamics,
ΔE = q + w = 0 + 24775.5 = 24775.5 J
Example 2. A certain volume of dry air at NTP is expanded reversibiy to four times its volume (a) isothermally (b) adiabatically. Calculate thefinal pressure and temperature in each case, assuming ideal behaviour.
(CP \ CV for air = 1.4)
Solution.
Let V1 be the initial volume of dry air at NTP.
(a) Isothermal expansion: During isothermal expansion, the temperature remains the same throughout. Hence, final temperature will be 273 K.
Since P1V1 = P2V2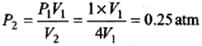
(b) Adiabatic expansion: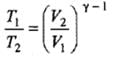
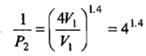
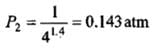
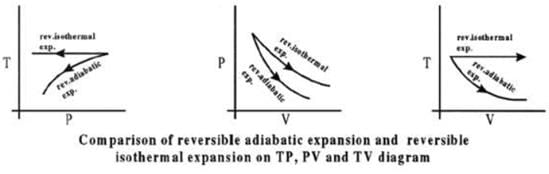
Comparison of Reversible Isothermal And Reversible Adiabatic Ideal Gas Expansion
Expansion
(i) If final volumes are same
Isothermal process.
P1v1 = Piso V2
⇒
Adiabatic process.
P1v1γ = Padia V2γ
⇒ Piso > Padia |
(ii) If final pressures are same
Isothermal process.
P1V1 = P2 Viso
.......(1)
P1V1γ = P2Vγ adia
In ideal gas expansion,
| Wiso | > | Wadia |
Hence
⇒ Viso > Vadia |
Compression
(i) If final volumes are same
For isothermal process
P1V1 = PisoV2
..........(1)
Adiabatic process.
P1V1γ = PadiaV2γ
..........(2)
Padia > Piso |
(ii) If final pressures are same
P1V1 = P2 Viso ..........(1)
P1V1γ = P2 Vγ adia ..........(2)
⇒
⇒
⇒ Vadia > Viso |
|
366 videos|847 docs|301 tests
|
FAQs on Enthalpy, Heat, Internal Energy & Work Done Calculations in Different Processes - Chemistry for JEE Main & Advanced
| 1. What is an adiabatic process in thermodynamics? |  |
| 2. How is enthalpy related to heat in thermodynamics? |  |
| 3. How can internal energy be calculated in an adiabatic ideal gas process? |  |
| 4. What is the work done in an adiabatic compression process of an ideal gas? |  |
| 5. How does the temperature change in an adiabatic expansion of an ideal gas? |  |
















